Forum » Znanost in tehnologija » Verjetnosti pri kartah
Verjetnosti pri kartah
Thomas ::
Kaj bi rad?
Sprašujem se, kaj je bolj verjetno. AAAA:FR, ali da nekdo napiše na forum, da se je to zgodilo.
Ti kaj ni prav?
Sprašujem se, kaj je bolj verjetno. AAAA:FR, ali da nekdo napiše na forum, da se je to zgodilo.
Ti kaj ni prav?
Man muss immer generalisieren - Carl Jacobi
itak37 ::
Ma neumnost. Težko, da se je v zgodovini Texay Holdem zgodilo več kot vsega parkrat, da je nekdo imel poker asov, drugi pa FR.
Težko, da se je 1X.
No modrina, pa povej KAKO je to možno pri Texay Holdem? Al kako se že tej igri reče? Kako je možen poker asov proti FR?
Dovolj majhna, da se v Sloveniji ni zgodila, dovolj majhna, da se tvojim inozemskim znancem ni zgodila. Dovolj majhna, da tak dogodek ni nikjer dokumentiran.
Torej se bo MORDA v 100 letih zgodilo FR:AAA.Hja. Lahko se zgodi. Samo ni preveč verjetno, da se bo v naslednje pol ure. Niti da se je že kdaj v SLO, internetne mize s Slovenci vključene.
Jaz tudi ne. Ker takih dogodkov kot FR:AAAA @ $100000 ni (bilo).
Preberi si svoje izjave. Kot je tvoja navada, začneš z absolutnimi trditvami o nečem, o čemer nimaš pojma.
Ne vem dosti o pokru. Ampak ... si se ti izkazal, v poznavanju tega primera, BISTVENO slabše od mene, miško.
Ko ti stvar razložijo in ti pojasnijo da je to možno, se pa začneš izmikat in spreminjat svoje trditve. Ne zmoreš pa priznati, da si se zmotil.
Thomas, you are FOS !!!
Težko, da se je 1X.
No modrina, pa povej KAKO je to možno pri Texay Holdem? Al kako se že tej igri reče? Kako je možen poker asov proti FR?
Dovolj majhna, da se v Sloveniji ni zgodila, dovolj majhna, da se tvojim inozemskim znancem ni zgodila. Dovolj majhna, da tak dogodek ni nikjer dokumentiran.
Torej se bo MORDA v 100 letih zgodilo FR:AAA.Hja. Lahko se zgodi. Samo ni preveč verjetno, da se bo v naslednje pol ure. Niti da se je že kdaj v SLO, internetne mize s Slovenci vključene.
Jaz tudi ne. Ker takih dogodkov kot FR:AAAA @ $100000 ni (bilo).
Preberi si svoje izjave. Kot je tvoja navada, začneš z absolutnimi trditvami o nečem, o čemer nimaš pojma.
Ne vem dosti o pokru. Ampak ... si se ti izkazal, v poznavanju tega primera, BISTVENO slabše od mene, miško.
Ko ti stvar razložijo in ti pojasnijo da je to možno, se pa začneš izmikat in spreminjat svoje trditve. Ne zmoreš pa priznati, da si se zmotil.
Thomas, you are FOS !!!
Thomas ::
>> Ker takih dogodkov kot FR:AAAA @ $100000 ni (bilo).
Seveda, da jih ni bilo. Še vedno ne. Ker tukajle so špilali za drobiž.
Če so špilali ... sploh.
Ampak četudi so, moja izjava še vedno stoji.
>> Ker takih dogodkov kot FR:AAAA @ $100000 ni (bilo).
Seveda, da jih ni bilo. Še vedno ne. Ker tukajle so špilali za drobiž.
Če so špilali ... sploh.
Ampak četudi so, moja izjava še vedno stoji.
>> Ker takih dogodkov kot FR:AAAA @ $100000 ni (bilo).
Man muss immer generalisieren - Carl Jacobi
itak37 ::
Final Pot: $382.10
To je priblizno 300 EUR. To je zate drobiž?
To se je zgodilo v NL200$, kar je za online srednji razred
Ker takih dogodkov kot FR:AAAA @ $100000 ni bilo
To si se spomnil na drugi strani debate, ko so ti razložili, za kaj se sploh gre, in si pogruntal da je to teoretično možno, in si zato spremenil svojo začetno trditev, da je to nemogoče.
Če so špilali ... sploh.
Kakšne dokaze pa sploh pričakuješ?
To je priblizno 300 EUR. To je zate drobiž?
To se je zgodilo v NL200$, kar je za online srednji razred
Ker takih dogodkov kot FR:AAAA @ $100000 ni bilo
To si se spomnil na drugi strani debate, ko so ti razložili, za kaj se sploh gre, in si pogruntal da je to teoretično možno, in si zato spremenil svojo začetno trditev, da je to nemogoče.
Če so špilali ... sploh.
Kakšne dokaze pa sploh pričakuješ?
Zgodovina sprememb…
- spremenil: itak37 ()
Thomas ::
Ja, iz klasičnega pokra ste presedlali na TH.
Samo tudi tu moja formulacija ni bila prekršena, še vedno ne.
Ker takih dogodkov kot FR:AAAA @ $100000 ni bilo
Če pa bodo, bom podvomil v poštenost igre. Ne boš zameru?
Ali pa če.
Samo tudi tu moja formulacija ni bila prekršena, še vedno ne.
Ker takih dogodkov kot FR:AAAA @ $100000 ni bilo
Če pa bodo, bom podvomil v poštenost igre. Ne boš zameru?
Ali pa če.
Man muss immer generalisieren - Carl Jacobi
itak37 ::
Ja, iz klasičnega pokra ste presedlali na TH.
Če pogledaš na wikkipedi geslo Poker, boš na prvi strani strani opazil sliko in pod njo ta napis:
A game of Texas hold'em, the most popular form of poker, in progress.
Texas Holdem je najbolj razširjena vrsta pokerja in v svetu je pod pojmom poker mišljen Texas Holdem.
Kaj pa je sploh "klasični poker"?
Kot sem ti že prej povedal, je ta tvoja formulacija nastala na drugi strani te teme, ko si pogruntal da govoriš neumnosti, in si spremenil začetno trditev namesto da bi priznal svojo zmoto. Če pogledaš svojo začetno trditev:
V eni temi se dva tipčka delata blazno pametna na mojo sicer obrobno pripombo, da ne verjamem pokerašu, da je imel eden poker asov, tadrugi pa flush royal.
niso nikjer omenjene nobene omejitve. Postopoma si pa začel še dodajati različne pogoje (lokacija, višina limitov).
Če pogledaš na wikkipedi geslo Poker, boš na prvi strani strani opazil sliko in pod njo ta napis:
A game of Texas hold'em, the most popular form of poker, in progress.
Texas Holdem je najbolj razširjena vrsta pokerja in v svetu je pod pojmom poker mišljen Texas Holdem.
Kaj pa je sploh "klasični poker"?
Kot sem ti že prej povedal, je ta tvoja formulacija nastala na drugi strani te teme, ko si pogruntal da govoriš neumnosti, in si spremenil začetno trditev namesto da bi priznal svojo zmoto. Če pogledaš svojo začetno trditev:
V eni temi se dva tipčka delata blazno pametna na mojo sicer obrobno pripombo, da ne verjamem pokerašu, da je imel eden poker asov, tadrugi pa flush royal.
niso nikjer omenjene nobene omejitve. Postopoma si pa začel še dodajati različne pogoje (lokacija, višina limitov).
Thomas ::
>> V eni temi se dva tipčka delata blazno pametna na mojo sicer obrobno pripombo, da ne verjamem pokerašu, da je imel eden poker asov, tadrugi pa flush royal.
To si lahko napišeš na strop in se naučiš, da je bistveno bolj verjetno da tipček laže, kot da se je to res zgodilo.
Dialekt pokra gor ali dol.
Sem dregnil ob kakšen verski simbol?
To si lahko napišeš na strop in se naučiš, da je bistveno bolj verjetno da tipček laže, kot da se je to res zgodilo.
Dialekt pokra gor ali dol.
Sem dregnil ob kakšen verski simbol?
Man muss immer generalisieren - Carl Jacobi
itak37 ::
Jest ti pa povem da to ni neverjetno, obstaja najmanj 10.000 možnih permutacij kart, pri katerih se to lahko zgodi.
Povem ti še to, da se delaš pametnega v stvareh, o katerih nimaš pojma.
Ko ti nekdo dokaže, da si se zmotil, se narediš neumnega in začneš obračat besede in se izgovarjat.
In ja, bolj bi verjel tistemu pokerašu kot tebi, ki karneki nabijaš o stvareh, o katerih nimaš blage veze.
Povem ti še to, da se delaš pametnega v stvareh, o katerih nimaš pojma.
Ko ti nekdo dokaže, da si se zmotil, se narediš neumnega in začneš obračat besede in se izgovarjat.
In ja, bolj bi verjel tistemu pokerašu kot tebi, ki karneki nabijaš o stvareh, o katerih nimaš blage veze.
Thomas ::
Kaj sploh hočeš? Reči da nisem imel prav, ko sem trdil da:
Ker takih dogodkov kot FR:AAAA @ $100000 ni bilo?
A? A to? Bodi on topic, pusti moje navade pri miru, ker so off topic, z mano vred!
Ker takih dogodkov kot FR:AAAA @ $100000 ni bilo?
A? A to? Bodi on topic, pusti moje navade pri miru, ker so off topic, z mano vred!
Man muss immer generalisieren - Carl Jacobi
Matev ::
če je teoretično možno da pride do tega
potem ne more nihče za nobeno igro dveh pokerašev vnaprej reči da ne bo imela takega razpleta
to pomeni da če greva jaz in še nekdo igrati poker
nihče ne more 100% trditi da ne bo končni rezultat FR:AAAA
potem ne more nihče za nobeno igro dveh pokerašev vnaprej reči da ne bo imela takega razpleta
to pomeni da če greva jaz in še nekdo igrati poker
nihče ne more 100% trditi da ne bo končni rezultat FR:AAAA
MadMicka ::
Ma kdo kak link do tabele za verjetnosti za TH? Npr., če imaš dva poba v roki, na mizi pa je en kralj in štiri nižje karte, potem še znaš na pamet na hitro oceniti, koliko je šans, da ima kdo od soigralcev kralja. Da bi bilo čim več značilnih situacij...
Thomas ::
> nihče ne more 100% trditi da ne bo končni rezultat FR:AAAA
Nihče niti ne more trditi, da nimaš doma tajne flote 99 Rolsrojsev.
Teoretično je povsem možno.
Vendar ko to nekdo razlaga da ima ... si skeptičen, ane. Še bolj bodi skeptičen, ko razlaga, da je imel FR:AAAA. Ker tisti s flotami avtomobilov dejansko obstajajo.
Nihče niti ne more trditi, da nimaš doma tajne flote 99 Rolsrojsev.
Teoretično je povsem možno.
Vendar ko to nekdo razlaga da ima ... si skeptičen, ane. Še bolj bodi skeptičen, ko razlaga, da je imel FR:AAAA. Ker tisti s flotami avtomobilov dejansko obstajajo.
Man muss immer generalisieren - Carl Jacobi
Matev ::
Nihče niti ne more trditi, da nimaš doma tajne flote 99 Rolsrojsev.
mislim da je veliko indicev ki govorijo proti temu
medtem ko izid pri kartah ni pogojen z ničemer
lahko nastane vsakomu in kadarkoli
veliko prej verjamem da dobim AAAA:FR (če začnem igrati poker in ga igram)
kot pa da bom imel 99 rojsrojsev
kadarkoli
Thomas ::
> lahko nastane vsakomu in kadarkoli
Lahko ti tudi kakšen sorodnik iz Amerike, o katerem nisi še nič slišal, v oporoki zapusti tisti floto.
Kadarkoli, komurkoli. Kako hudo verjetno je to, je pa drugo vprašanje.
Mnogi so v Texas Holdem obogateli. Na FR:AAAAA pri 100000$ ali več pa še čakamo.
Lahko ti tudi kakšen sorodnik iz Amerike, o katerem nisi še nič slišal, v oporoki zapusti tisti floto.
Kadarkoli, komurkoli. Kako hudo verjetno je to, je pa drugo vprašanje.
Mnogi so v Texas Holdem obogateli. Na FR:AAAAA pri 100000$ ali več pa še čakamo.
Man muss immer generalisieren - Carl Jacobi
Matev ::
Nihče niti ne more trditi, da nimaš doma tajne flote 99 Rolsrojsev.
no pa naj kdo zračuna za FR:AAAAA
kolikšna je verjetnost za pojav
vsa priemrjava z flotami rojsrojsev je telebajščina
Thomas ::
Sej smo že izračunali. Ciki57 in jaz sva dobila podobne rezultate.
Potrudi se višje gor!
Potrudi se višje gor!
Man muss immer generalisieren - Carl Jacobi
frudi ::
lol... 'the mouth' je sigurno imel kaj lepega za povedat po tem riverju 
1ACDoHVj3wn7N4EMpGVU4YGLR9HTfkNhTd... in case I've written something useful :)
horsovski ::
Vidim, da je kar nekaj zainteresinah tukaj za poker.
Ob tem bi vam povedal za novo slovensko stran www.poker-business.net/slo
lp
p.s upam da je to v skladu s pravili
Ob tem bi vam povedal za novo slovensko stran www.poker-business.net/slo
lp
p.s upam da je to v skladu s pravili
Gizm0 ::
I was amused by the comment Mike Matusow made when he was asked how he felt about winning and losing a million online in the span of a couple of days. He said, "It's just numbers on a computer screen."
jRk0 ::
kaksna je verjetnost, da smo vceraj v poker klubu na ptuju, ki obratuje vse skupaj 2 dni, od tega je 1. dan bla otvoritev, ze videli Royal-a :) pa smo ga, jebi ga, verjetnost je majhna, pride pa lahko kadarkoli.
You fuck up once, you loose two teeth.
Thomas ::
Verjetnost da ste videli nenaštimanega Royala je manjaša, kot da ste videli Royala in je bil naštiman.
Thomas Bayes.
Thomas Bayes.
Man muss immer generalisieren - Carl Jacobi
T0RN4D0 ::
Nisem vsega prebral ampak pri texas hold'em (večinoma se igra to) je zadeva čist lepo izvedljiva, ker je 5 kart od obeh... => Pa čeprav je možnost 1:miljonmiljard :)
Matev ::
Pravzaprav je katerakoli razdelitev, ki pade skoraj nemogoča, da pade v takem zaporedju kot je padla.
jRk0 ::
Thomas, to si ga pa mimo pihnil :)
verjetnost da je royal bil nastiman je 0%. ne 0,xxxxx1, ampak tocno 0, ker ne mores nikakor nastimat tega. razen kaksen "carodej" , ta dilerka pa zagotovo ne =)
verjetnost da je royal bil nastiman je 0%. ne 0,xxxxx1, ampak tocno 0, ker ne mores nikakor nastimat tega. razen kaksen "carodej" , ta dilerka pa zagotovo ne =)
You fuck up once, you loose two teeth.
Zgodovina sprememb…
- spremenilo: jRk0 ()
Thomas ::
Čemu boš zdaj bolj verjel? Svojim očem ali mojemu teoretičnemu razglabljanju?
Jaz bi bolj verjel svojemu znanju verjetnosti, kot svojim lastnim očem. Oziroma, bi iskal bolj verjetne razlage kot je ta, da se je kar na prvi dan/teden igralnice slučajno pojavil nek Flush Royal.
Jaz bi bolj verjel svojemu znanju verjetnosti, kot svojim lastnim očem. Oziroma, bi iskal bolj verjetne razlage kot je ta, da se je kar na prvi dan/teden igralnice slučajno pojavil nek Flush Royal.
Man muss immer generalisieren - Carl Jacobi
c3p0 ::
NB: Heads-up poker is the form of the game where bots are the most formidable, in which mathematical analysis and game theory can make a programmed player's game virtually unassailable.
Ni neke revolucionarne AI pri heads-up in pri limit igri. Drugo je NL igra proti večim ali višji limiti, kjer boti zaenkrat nimajo šans. Se pa na univerzi v Alberti mantrajo z enim takim projektom:
http://www.cs.ualberta.ca/~games/poker/FAQ.html
Thomas ::
Ni vprašanje. Next big thing je kar RPSOP. Go bomo spustili.
Man muss immer generalisieren - Carl Jacobi
Zgodovina sprememb…
- spremenil: Thomas ()
mgermo ::
500 handov kolikor so odigral pomeni manj kot nič.
Na letošnjem WSOP je bil AAAA vs royal.
Na letošnjem WSOP je bil AAAA vs royal.
Thomas ::
500 handov kolikor so odigral pomeni manj kot nič.
Pomeni dovolj, da je jasno, kako je. Še eno upanje nazadnjakov je na tem, da ugasne, če že ni ugasnilo.
Na letošnjem WSOP je bil AAAA vs royal.
No shit?
Man muss immer generalisieren - Carl Jacobi
mgermo ::
1. 500 handov je manj kot 1 ura online. Če folk na mesec dela 100k handov in več in je možno da runnaš bad nekaj 10k handov, 500 handov nima pomena one way or another.
2. ? koliko vem si ravno ti zatrjeval kako quadsi vs royal never happen in če se zgodi je pa rigged.
2. ? koliko vem si ravno ti zatrjeval kako quadsi vs royal never happen in če se zgodi je pa rigged.
Thomas ::
1. ... kr tolaži se.
2. Seveda. Bolj verjetno je, da gre za fejk. Thomas Bayes.
2. Seveda. Bolj verjetno je, da gre za fejk. Thomas Bayes.
Man muss immer generalisieren - Carl Jacobi
Barakuda1 ::
Bolj verjetno je, da gre za fejk. Thomas Bayes.
Bolj verjetno že, ne pa tudi nemogoče.
A ker se je zgodilo nekaj kar je "bolj verjetno", je pač edn orng izgubil. Jebat ga, pač ni vse v verjetnostih
Gizm0 ::
Igralo se je heads-up limit holdem poker. Sami boji pa so potekali na naslednji način. Vedno sta se igrala 2 matcha hkrati, vsakič po 500 istih handov. Se pravi v matchu 1 je Polaris dobil iste hande kot jih je dobil človek v matchu 2. Seveda ni niti Polaris niti človek vedel, kaj se dogaja v sosednji sobi. Na takšen način so zelo zmanjšali varianco, tako da je 500 handov dalo že dokaj natančen rezultat. Polaris je zmagal 2-1-1, za zmago pa se je štelo, če je na koncu dneva kdo imel več kot 25 malih stav prednosti. Bilo je dokaj izenačeno, največja prednost Polarisa je ta, da on ne "tilta" niti kadar je zelo v minusu ali kadar je zelo v plusu. Igra torej vedno tisto svojo optimalno igro, kar za človeka ne moremo reči. Je pa vprašanje, če bi igrali za pravi denar, ali bi avtorji Polarisa naredili kakšno napako pri samem dizajnu, ko je v igri nekaj 100k$ :P
Polaris je laufal na enem samem macbook proju, torej glede same surove moči sploh ni problem Polarisa. Kar je njegov glavni problem, oz. problem vseh ostalih botov, da še vedno ne zna igrati, kadar sta v igri več kot 2 igralca. Če igrajo trije, potem bot nima nobenih možnosti. Prav tako ne zna igrati no-limit holdema, kjer stave niso fixne. Drugače pa je že par let nazaj bot bil zelo konkurenčen v samem heads-up limit holdemu, samo da takrat matchi niso bili tako medijsko pokriti.
So pa sami handi objavljeni na http://www.stoxpoker.com/man_vs_machine... ter na http://www.cs.ualberta.ca/~games/poker/...
Polaris je laufal na enem samem macbook proju, torej glede same surove moči sploh ni problem Polarisa. Kar je njegov glavni problem, oz. problem vseh ostalih botov, da še vedno ne zna igrati, kadar sta v igri več kot 2 igralca. Če igrajo trije, potem bot nima nobenih možnosti. Prav tako ne zna igrati no-limit holdema, kjer stave niso fixne. Drugače pa je že par let nazaj bot bil zelo konkurenčen v samem heads-up limit holdemu, samo da takrat matchi niso bili tako medijsko pokriti.
So pa sami handi objavljeni na http://www.stoxpoker.com/man_vs_machine... ter na http://www.cs.ualberta.ca/~games/poker/...
c3p0 ::
500 handov je pri pokru statistično 0. 50k je recimo za silo.
Šlo pa je za limit igro, kjer je število možnih potez zelo omejeno.
"The Man Machine Event is a competition pitting a team of Poker players against the University of Alberta's advanced poker bot Polaris. The game is a $500/$1000 Limit Heads Up Texas Holdem, with a duplicate reverse match system (the same cards are dealt in both games but the human and bot is reversed in the second match)."
Šlo pa je za limit igro, kjer je število možnih potez zelo omejeno.
"The Man Machine Event is a competition pitting a team of Poker players against the University of Alberta's advanced poker bot Polaris. The game is a $500/$1000 Limit Heads Up Texas Holdem, with a duplicate reverse match system (the same cards are dealt in both games but the human and bot is reversed in the second match)."
strictom ::
Je bil primer pri Texas Hold'em pokru ko sem imel 2x poker v eni igri. Poker v pobih in v desetkah. Potem pa 2x zapored flush.
"Violence is the last refuge of the incompetent" - Salvor Hardin
Barakuda1 ::
Je bil primer pri Texas Hold'em pokru ko sem imel 2x poker v eni igri.
A res???
Ejjj, to kombinacijo bi pa res rad videl (vsaj napisano)
Mal nakladanja je lohk zabavno, tolk pa spet ne.
Gizm0 ::
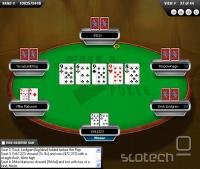
Dogaja se vse mogoče  Ker ta forum ne pozna prijaznega formata za pretvorjene hande, prilagam sliko. V razmaku 20 minut, 2x quads z 99 za isto mizo:
Ker ta forum ne pozna prijaznega formata za pretvorjene hande, prilagam sliko. V razmaku 20 minut, 2x quads z 99 za isto mizo:
Kar je dokaj neverjetno je tudi to, da sem obakrat dobil stack od nekoga. Kadar ti zadaneš quads, je toliko manjša verjetnost, da je nasprotnik tudi kaj zadel.
Drugače pa ja, večja verjetnost je, da se je nekdo na tem forumu neko stvar preprosti izmislil, kot pa da se je to dejansko zgodilo.
Kar je dokaj neverjetno je tudi to, da sem obakrat dobil stack od nekoga. Kadar ti zadaneš quads, je toliko manjša verjetnost, da je nasprotnik tudi kaj zadel.
Drugače pa ja, večja verjetnost je, da se je nekdo na tem forumu neko stvar preprosti izmislil, kot pa da se je to dejansko zgodilo.
strictom ::
Barakuda1, res. Ne nakladam. Prvo sem dobil 2 poba. Potem v flopu pade en pob in na koncu še v riverju. Zajebal sem edino ker sem nespametno stavil all-in in je večina odstopla. Dobil sem pač male pare :)
Pri desetkah je blo pa da sem mel 10 in kraljico v roki in pade potem tris desetk. Pač sumil sem da ma kolega lestvico in sem odstopil. Potem pa pade še zadnja desetka in sem se lahko sam tepo po glavi. Jebiga.
Z kolegi igramo poker like 2, 3 mesce in noben še nikol ni imel pokra, jaz sem ga pač v eni igri dobil dvakrat.
Pri desetkah je blo pa da sem mel 10 in kraljico v roki in pade potem tris desetk. Pač sumil sem da ma kolega lestvico in sem odstopil. Potem pa pade še zadnja desetka in sem se lahko sam tepo po glavi. Jebiga.
Z kolegi igramo poker like 2, 3 mesce in noben še nikol ni imel pokra, jaz sem ga pač v eni igri dobil dvakrat.
"Violence is the last refuge of the incompetent" - Salvor Hardin
c3p0 ::
Verjetno je "igra" razumel kot en hand, kjer seveda en igralec ne more imeti dveh pokrov hkrati. Šlo bi, če bi bilo 6 kart na mizi.

#000000 ::
Sta igrala sir oliver in nosati bob ter oba imela poker v asih.
Zmagal je sir oliver, pošto je držao karte u lijevoj ruci :)
Zmagal je sir oliver, pošto je držao karte u lijevoj ruci :)
Roadkill ::
Sam ena taka za štos:
Zanimivo je, da je veliko bolj vrjetno, da imaš v roki Flush Royal, ko ima tvoj nasprotnik AAAA, kakor takrat ko ima nasprotnik 9999....2222. :)
Zanimivo je, da je veliko bolj vrjetno, da imaš v roki Flush Royal, ko ima tvoj nasprotnik AAAA, kakor takrat ko ima nasprotnik 9999....2222. :)
Ü
Barakuda1 ::
Verjetno je "igra" razumel kot en hand, kjer seveda en igralec ne more imeti dveh pokrov hkrati.
ja čudno.; kako pa naj bi ga drugače razumel.
Če pa hočete nenavadne anekdote (iz resničnih iger) pa vam povem eno, ki sem ji bil priča pred kakšnima dvema tednoma.
Igralec (na turnirju) izloči igralca, ki ima ful (K, K, 4,4,4) s pokrom 4 (tris četvork je padel v flopu).
V finalni igri (ostali so še 4 igralci) pa sam izpade, s točno enako kobinacijo, le da ima tokrat sam ful, nasprotnik pa poker. Da je ironija večja, se kombinacija dobesedno ponovi (edino za barvo kraljev nisem siguren)
Ja vem, sliš se neverjetno, a zgodilo se je na enam samem turnirju.
c3p0 ::
Just for fun... Na zadnjem WSOP main eventu, je en igralec na riveru dobil poker asov, drugi pa royal flush. Pokazano po TV.
Možnosti za kaj takega so, tako oni, 1:2.700.000.000
So pa mizo snemali le zato, ker je za njo sedel tudi znani h'woodski sitcom igralec Ray Romano (ki pa ni bil udeležen v handu ;).
Možnosti za kaj takega so, tako oni, 1:2.700.000.000
So pa mizo snemali le zato, ker je za njo sedel tudi znani h'woodski sitcom igralec Ray Romano (ki pa ni bil udeležen v handu ;).
Zgodovina sprememb…
- spremenil: c3p0 ()
Thomas ::
Ja, jaz zgodbi ne verjamem. Dosti bolj verjetno je da je bila lažirana, kot da je bilo res.
Ampak vsak po svoji pameti. Tvoja glava, tvoj svet.
Ampak vsak po svoji pameti. Tvoja glava, tvoj svet.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Denimo, da imamo 10 000 "high fly" posnetkov raznih "poker world cup open" partij, na youtube in podobnih mestih, v zadnjih 10 letih. Po moje je to kar dobra ocena.
Poker asov proti royalu, bi pričakovali šele na kakšnem milijardotem posnetku. Ali drugače rečeno, po kakem milijonu let odvijanja teh "poker world cup opens" in pridnega snemanja na youtube.
Milijon let prezgodaj torej. Prepuščam naivcem, da to verjamejo. Posebno še, ker je pa TAKO LAHKO lažirati tako partijo, s strani delilca kart.
Kompulzivni naivci, kompulzivni iracionalisti in kompulzivni pokeraši - se z mano ne bodo strinjali. Nasprotno. Od njih pričakujem močan emocionalni odziv, poln negativnih čustev do moje skromne osebe.
Povsem predvidljivo. Tako mora biti!
Poker asov proti royalu, bi pričakovali šele na kakšnem milijardotem posnetku. Ali drugače rečeno, po kakem milijonu let odvijanja teh "poker world cup opens" in pridnega snemanja na youtube.
Milijon let prezgodaj torej. Prepuščam naivcem, da to verjamejo. Posebno še, ker je pa TAKO LAHKO lažirati tako partijo, s strani delilca kart.
Kompulzivni naivci, kompulzivni iracionalisti in kompulzivni pokeraši - se z mano ne bodo strinjali. Nasprotno. Od njih pričakujem močan emocionalni odziv, poln negativnih čustev do moje skromne osebe.
Povsem predvidljivo. Tako mora biti!
Man muss immer generalisieren - Carl Jacobi
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Poker (strani: 1 2 3 4 5 )Oddelek: Loža | 32614 (2149) | Randomness |
| » | Izgubili smo še v pokru (strani: 1 2 )Oddelek: Novice / Znanost in tehnologija | 22013 (18383) | leiito |
| » | Računalnik in človek v pokru statistično izenačenaOddelek: Novice / Znanost in tehnologija | 24343 (17731) | oemdzi |
| » | Online gambling in davek?! (strani: 1 2 )Oddelek: Loža | 17887 (13980) | superman |
| » | gembling (strani: 1 2 )Oddelek: Znanost in tehnologija | 11879 (7960) | c3p0 |