Forum » Loža » Nicely distributed circles
Nicely distributed circles

BRBR ::
Nekoč sem naletel na online prog. (algoritem), ki je zrisal kroge, v 2D ravnino, distribuirane v smislu 'zlatega reza'.
Ne najdem, če kdo ve kje to je ?
Nekaj takega, s tem da je zrisal cele kroge, brez teh, ki sekajo meje.
Ne najdem, če kdo ve kje to je ?
Nekaj takega, s tem da je zrisal cele kroge, brez teh, ki sekajo meje.
Never underestimate the power of idiots in large groups.
sbawe64 ::
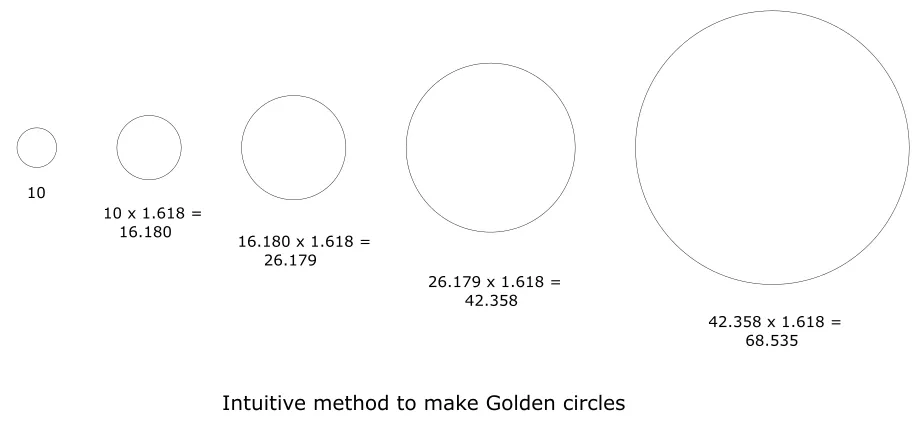
Iščeš algoritem, ki naredi kroge z Golden Ratio razmerjem med njimi v 2d ravnini, tako kot so tu narisani ?
https://medium.com/@prozeegames/making-...
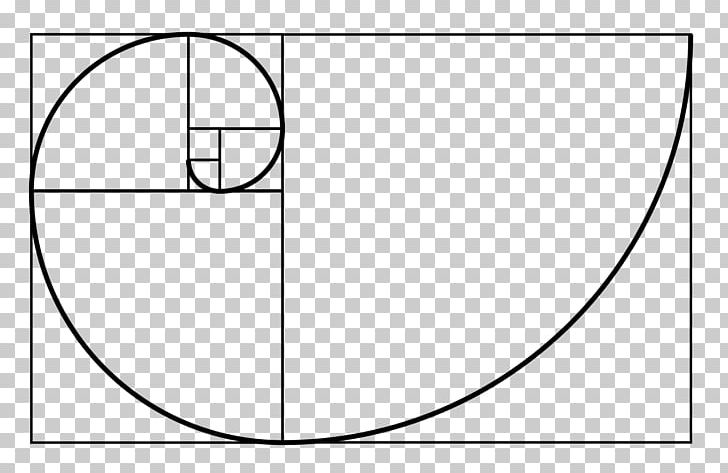
Ali bi rad kroge umestil po ravnini po Golden Ratio krivulji ?
https://medium.com/@prozeegames/making-...
Ali bi rad kroge umestil po ravnini po Golden Ratio krivulji ?
2020 is new 1984
Corona World order
Corona World order
sbawe64 ::
Phind
To create a pattern of nicely distributed circles of different sizes with a golden ratio pattern on a 2D plane, you can follow a method inspired by the Fibonacci sequence and the golden ratio. The golden ratio, approximately 1.618, can be used to calculate the size of each subsequent circle based on the size of the previous circle. This method allows for the creation of a visually pleasing and harmonious arrangement of circles.
Here's a step-by-step algorithm to achieve this:
1. **Start with a base circle**: Choose a size for your first circle. This will be the starting point of your pattern.
2. **Calculate the size of the next circle using the golden ratio**: Multiply the radius of the current circle by the golden ratio (approximately 1.618) to find the radius of the next circle. This ensures that each circle's size is a multiple of the golden ratio, creating a visually appealing pattern.
3. **Align the circles**: Place the circles in a way that aligns with the golden ratio pattern. This could be in a grid pattern or any other arrangement that visually represents the golden ratio. For example, you could arrange the circles in a way that each circle's center is aligned with the centers of two adjacent circles, creating a pattern that resembles a honeycomb or a Fibonacci spiral.
4. **Iterate**: Repeat steps 2 and 3 to create as many circles as needed, each time using the golden ratio to calculate the size of the next circle.
Here's a simple example in pseudocode to illustrate the algorithm:
```python
def create_golden_ratio_pattern(base_radius, num_circles):
golden_ratio = 1.618
base_x, base_y = 0, 0 # Starting point for the first circle
circles = []
for i in range(num_circles):
radius = base_radius * (golden_ratio ** i)
x, y = base_x, base_y # Adjust x, y based on your pattern's requirements
circles.append((x, y, radius))
return circles
# Example usage
base_radius = 10
num_circles = 10
pattern = create_golden_ratio_pattern(base_radius, num_circles)
# Now you have a list of tuples, each containing the x, y coordinates and radius of each circle
```
koda
https://pastebin.com/iifj6xSb
This algorithm starts with a base circle and uses the golden ratio to calculate the size of each subsequent circle. The `create_golden_ratio_pattern` function generates a list of tuples, each containing the x, y coordinates and radius of each circle in the pattern. You can adjust the starting point (`base_x`, `base_y`) and the pattern's layout to fit your specific requirements.
Remember, the arrangement of the circles (how they are aligned and positioned relative to each other) is crucial for achieving a visually pleasing pattern. Experiment with different layouts to find the one that best suits your needs.
To create a pattern of nicely distributed circles of different sizes with a golden ratio pattern on a 2D plane, you can follow a method inspired by the Fibonacci sequence and the golden ratio. The golden ratio, approximately 1.618, can be used to calculate the size of each subsequent circle based on the size of the previous circle. This method allows for the creation of a visually pleasing and harmonious arrangement of circles.
Here's a step-by-step algorithm to achieve this:
1. **Start with a base circle**: Choose a size for your first circle. This will be the starting point of your pattern.
2. **Calculate the size of the next circle using the golden ratio**: Multiply the radius of the current circle by the golden ratio (approximately 1.618) to find the radius of the next circle. This ensures that each circle's size is a multiple of the golden ratio, creating a visually appealing pattern.
3. **Align the circles**: Place the circles in a way that aligns with the golden ratio pattern. This could be in a grid pattern or any other arrangement that visually represents the golden ratio. For example, you could arrange the circles in a way that each circle's center is aligned with the centers of two adjacent circles, creating a pattern that resembles a honeycomb or a Fibonacci spiral.
4. **Iterate**: Repeat steps 2 and 3 to create as many circles as needed, each time using the golden ratio to calculate the size of the next circle.
Here's a simple example in pseudocode to illustrate the algorithm:
```python
def create_golden_ratio_pattern(base_radius, num_circles):
golden_ratio = 1.618
base_x, base_y = 0, 0 # Starting point for the first circle
circles = []
for i in range(num_circles):
radius = base_radius * (golden_ratio ** i)
x, y = base_x, base_y # Adjust x, y based on your pattern's requirements
circles.append((x, y, radius))
return circles
# Example usage
base_radius = 10
num_circles = 10
pattern = create_golden_ratio_pattern(base_radius, num_circles)
# Now you have a list of tuples, each containing the x, y coordinates and radius of each circle
```
koda
https://pastebin.com/iifj6xSb
This algorithm starts with a base circle and uses the golden ratio to calculate the size of each subsequent circle. The `create_golden_ratio_pattern` function generates a list of tuples, each containing the x, y coordinates and radius of each circle in the pattern. You can adjust the starting point (`base_x`, `base_y`) and the pattern's layout to fit your specific requirements.
Remember, the arrangement of the circles (how they are aligned and positioned relative to each other) is crucial for achieving a visually pleasing pattern. Experiment with different layouts to find the one that best suits your needs.
2020 is new 1984
Corona World order
Corona World order
Zgodovina sprememb…
- spremenilo: sbawe64 ()

BRBR ::
Da še malo bolj specificiram, ali pa še enkrat. Evo, enkrat v enem chatu, sem poslal sliko. Tule če bi z miško lahko vlekel velike kroge jih ne bi mogel premaknit kamorkoli, malo magnetnega odboja bi lahko temu rekel. Neodvisno a so mali krogci tam ali ne. Domnevno sem tole zgeneriral s temle: link (harmonic looking result)
Če se komu da sprobat, meni na win7 ne dela, a bi moral nekam prilepit ene libraries, ki so spodaj omenjene ?
Če se komu da sprobat, meni na win7 ne dela, a bi moral nekam prilepit ene libraries, ki so spodaj omenjene ?
Never underestimate the power of idiots in large groups.
Zgodovina sprememb…
- spremenil: BRBR ()
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | GTa IV (strani: 1 2 )Oddelek: Igre | 9699 (8018) | jamiroq |
| » | Glasbeni izrazi v angleščiniOddelek: Sedem umetnosti | 7067 (6681) | embe |
| » | 24 inch lcdOddelek: Strojna oprema | 2768 (1680) | Mih@@ |
| ⊘ | Žitni krogi, ki so postali tema o Piramidah (strani: 1 2 3 4 5 6 7 8 )Oddelek: Loža | 33746 (28330) | Stepni Volk |
| » | invertiran zvokOddelek: Znanost in tehnologija | 2385 (1992) | CaqKa |