Forum » Znanost in tehnologija » Vprašanje neskončnosti
Vprašanje neskončnosti
pramarko ::
Tule sva z bratrancem po dveh [khemmm] prišla na težko debato o neskončnosti v povezavi z matematiko. (ok in o neskončnosti nasploh). Zdi se , da skuša matematika vriniti pojem neskončnosti v skupino številk. Primer je konvergiranje vrste 1/0, za katero da matematika suhoparen odgovor, da vrsta konvergira v neskončno. Kako razlaga neskončnost? Kaj je neskončnost?
Kolikor se spomnim iz ur matematike je bilo tudi nekaj besed o tem, da neskončnost sploh ne obstaja. Paradox? Kako je potem definirana zveznost?
Zdi se, da se matematika v prenekaterem primeru izogiba dejanskemu odgovoru na vprašanje s pojmom neskončnosti. A je tukaj matematika prešla v slepo ulico, kjer ne najde rešitve? Je potemtakem matematika na tem nivoju še kredibilno orodje s katerim lahko operiramo? Matematika nas očitno precej omejuje in nam ne daje vseh odgovorov.
Potrebuje matematika bugfix... ali pa bi bil bolj primeren kar Service Pack? Morda kar nov "operacijski sistem" :)
Kolikor se spomnim iz ur matematike je bilo tudi nekaj besed o tem, da neskončnost sploh ne obstaja. Paradox? Kako je potem definirana zveznost?
Zdi se, da se matematika v prenekaterem primeru izogiba dejanskemu odgovoru na vprašanje s pojmom neskončnosti. A je tukaj matematika prešla v slepo ulico, kjer ne najde rešitve? Je potemtakem matematika na tem nivoju še kredibilno orodje s katerim lahko operiramo? Matematika nas očitno precej omejuje in nam ne daje vseh odgovorov.
Potrebuje matematika bugfix... ali pa bi bil bolj primeren kar Service Pack? Morda kar nov "operacijski sistem" :)
Thomas ::
Moja milost so finitist. Nič ne dajo na "neskončnost", imajo jo za magijo, tako kot je rekel že Karl F. Gauss.
Bugfix, ja!
p.s.
Jasno, moje povsem neuradno mnenje.
Bugfix, ja!
p.s.
Jasno, moje povsem neuradno mnenje.
Man muss immer generalisieren - Carl Jacobi
pramarko ::
Thomas, k si lih eden najaktivnejših piscev v Sci-Tech forumu, kako si pa ti razlagaš neskončnost?
Kaj nima nihče drug nobenega komentarja???
Kaj nima nihče drug nobenega komentarja???
Marjan ::
Pramarko, v Z&T oddelku smo na temo neskončnosti že ogromno povedal.
Npr. tudi v tej temi: http://slo-tech.com/script/forum/izpisteme.shtml?threadID=35290#neprebrano.
Skratka, do sedaj v realnosti niso našli še nič neskončnega, in ti povem, da tudi ne bodo.
Npr. tudi v tej temi: http://slo-tech.com/script/forum/izpisteme.shtml?threadID=35290#neprebrano.
Skratka, do sedaj v realnosti niso našli še nič neskončnega, in ti povem, da tudi ne bodo.
drejc ::
Transcendentna števila (pi,e) imajo poljubno veliko decimalk
Če šteješ za končnost množico vseh atomov in manjših delcev vesolja, je množica (neponavljajočega zaporedja) decimalk pija še vedno večja. Je to neskončnost? IMO je. Vsaj jest tako razmišljam.
Neskončnost lahko formuliraš kot zgoraj (poljubno mnogo), preko vseh meja,...
Na drugi del tvojega posta naj omenim, da matematika ni znanost. Je več kot znanost, saj je osnova VSEM naravoslovnim znanostim.
Potrebuje matematika bugfixe? Vrjetno jih, saj obsežnejše (in tudi starejše) znanosti ljudje ne poznamo.
Matematika v prvem smislu ne opisuje narave, le abstraktne modele. Obstajajo pa matematični objekti, ki jih "po čudežu" najdemo tudi v naravi. Recimo zlati rez, čebele vedo zakaj je treba delat panj v obliki šestkotnikov,... skratka zabavni del matematike. Z drugim se niti ni treba obremenjevat, če matematike ne študiraš. Rajš se drž programiranja, je bolj "zemeljsko".

Če šteješ za končnost množico vseh atomov in manjših delcev vesolja, je množica (neponavljajočega zaporedja) decimalk pija še vedno večja. Je to neskončnost? IMO je. Vsaj jest tako razmišljam.
Neskončnost lahko formuliraš kot zgoraj (poljubno mnogo), preko vseh meja,...
Na drugi del tvojega posta naj omenim, da matematika ni znanost. Je več kot znanost, saj je osnova VSEM naravoslovnim znanostim.
Potrebuje matematika bugfixe? Vrjetno jih, saj obsežnejše (in tudi starejše) znanosti ljudje ne poznamo.
Matematika v prvem smislu ne opisuje narave, le abstraktne modele. Obstajajo pa matematični objekti, ki jih "po čudežu" najdemo tudi v naravi. Recimo zlati rez, čebele vedo zakaj je treba delat panj v obliki šestkotnikov,... skratka zabavni del matematike. Z drugim se niti ni treba obremenjevat, če matematike ne študiraš. Rajš se drž programiranja, je bolj "zemeljsko".
Thomas ::
Tkole ti bom povedal drejc!
Imaš znanstvenika ki raziskuje matematiko. Recimo mu Matematik. Pa imaš znanstvenika, ki raziskuje človeške možgane, do kvečjemu molekularnega nivoja dol. Recimo mu Nevrolog.
Vse kar bo odkril Matematik, bo odkril tudi Nevrolog! Oziroma, Nevrolog bo odkril nekoliko več. Še nematematična razmišljanja zraven. V dovolj dolgem času, se razume.
Celo Ceprogramer bo odkril vse, kar lahko odkrijeta onadva.
Computational equivalence, ene sorte.
Drži?
Imaš znanstvenika ki raziskuje matematiko. Recimo mu Matematik. Pa imaš znanstvenika, ki raziskuje človeške možgane, do kvečjemu molekularnega nivoja dol. Recimo mu Nevrolog.
Vse kar bo odkril Matematik, bo odkril tudi Nevrolog! Oziroma, Nevrolog bo odkril nekoliko več. Še nematematična razmišljanja zraven. V dovolj dolgem času, se razume.
Celo Ceprogramer bo odkril vse, kar lahko odkrijeta onadva.
Computational equivalence, ene sorte.
Drži?
Man muss immer generalisieren - Carl Jacobi
miwche ::
ne razumem. Ali bi Nevrolog odkril tudi kar bi odkril Matematik ali bi odkril le matematična in še nematematična razmišljanja poleg tega? bi lahko odkril kreativno razmišljanje?
bi lahko odkril vsebino razmišljanja?
potem bi pomenilo, da Nevrolog lahko odkrije še razmišljanja o katerih ne razmišljamo.
bi lahko odkril vsebino razmišljanja?
potem bi pomenilo, da Nevrolog lahko odkrije še razmišljanja o katerih ne razmišljamo.
Thomas ::
Ja, če goni simulacijo človeških možganov, bo videl vse, kar se tam dogaja.
Man muss immer generalisieren - Carl Jacobi
Cofko Cof ::
Še en paradox u zvezi z neskončnostjo.Imamo nek krog.Če je radij majhen je naprimer en centimeter dolg odsek na krogu zelo ukrivljen.Glede na to da je ukrivljenost obratno sorazmerna radiju se postavi vprašanje kaj dobimo če pošlemo radij u neskončnost?Krog katerga odseki niso čisto nič ukrivljeni, torej čisto navadno premico:)
fogl ::
To pa ni res...še vedno je krožnica. Kaj pa če imamo daljico, in jo damo na pol, in potem tisto polovico spet na pol...in to delamo v neskončnost...kaj dobimo...nič  Še vedno je daljica.
Še vedno je daljica.
Matematika je dogovor...kakor so se dogovorili tako pa je. Kaj pa so se dogovorili za neskončnost pa poglej tukaj.
Matematika je dogovor...kakor so se dogovorili tako pa je. Kaj pa so se dogovorili za neskončnost pa poglej tukaj.
lp, klemen
pramarko ::
>> To pa ni res...še vedno je krožnica.
Hmm... vprašanje, če je še krožnica. Koeficient ukrivljenosti namreč limitira v 0 (ko radij -> neskončnost). Kako je definirana krožnica? Če krožnica ni pogojena s koeficientom ukrivljenosti, potem se morda res imenuje krožnica, sicer pa ne.
>> Kaj pa če imamo daljico, in jo damo na pol, in potem tisto polovico spet na pol...in to delamo v neskončnost...kaj dobimo...nič Še vedno je daljica.
No, ravno take situacije mi niso povsem jasne! Neskončnost si dostikrat predstavljamo kot neko megagromozansko število, vendar se v neskončnosti začno dogajati razne "čudne" stvari - raje jih poimenujmo izjeme - drugače od rezultatov računanja z realnimi števili.
>> Matematika je dogovor...kakor so se dogovorili tako pa je. Kaj pa so se dogovorili za neskončnost pa poglej tukaj.
Se ti ne zdi, da so se bolj malo dogovorili in da ta dogovor bolj malo pove o neskončnosti sami?
Wolfram v NKS piše, da obstaja več vrst neskončnosti (str. 1162), kar je dodaten razlog, da neskončnosti ne moremo obravnavati preprosto kot neke megagromozanske številke. Žal nisem dovolj vešč matematike+angleščine, da bi po 1x branju razumel celotno poglavje o transfinitivnih številih, časa za globlje študije o tem pa tudi nimam. A je kdo dovolj domač v NKS, da bi lahko kolikor se da poljudno povedal, kaj Wolfram piše o neskončnosti?
Hmm... vprašanje, če je še krožnica. Koeficient ukrivljenosti namreč limitira v 0 (ko radij -> neskončnost). Kako je definirana krožnica? Če krožnica ni pogojena s koeficientom ukrivljenosti, potem se morda res imenuje krožnica, sicer pa ne.
>> Kaj pa če imamo daljico, in jo damo na pol, in potem tisto polovico spet na pol...in to delamo v neskončnost...kaj dobimo...nič Še vedno je daljica.
No, ravno take situacije mi niso povsem jasne! Neskončnost si dostikrat predstavljamo kot neko megagromozansko število, vendar se v neskončnosti začno dogajati razne "čudne" stvari - raje jih poimenujmo izjeme - drugače od rezultatov računanja z realnimi števili.
>> Matematika je dogovor...kakor so se dogovorili tako pa je. Kaj pa so se dogovorili za neskončnost pa poglej tukaj.
Se ti ne zdi, da so se bolj malo dogovorili in da ta dogovor bolj malo pove o neskončnosti sami?
Wolfram v NKS piše, da obstaja več vrst neskončnosti (str. 1162), kar je dodaten razlog, da neskončnosti ne moremo obravnavati preprosto kot neke megagromozanske številke. Žal nisem dovolj vešč matematike+angleščine, da bi po 1x branju razumel celotno poglavje o transfinitivnih številih, časa za globlje študije o tem pa tudi nimam. A je kdo dovolj domač v NKS, da bi lahko kolikor se da poljudno povedal, kaj Wolfram piše o neskončnosti?
Thomas ::
Najprej je ležeča osmica. Dve, plus in minus. To sta k realnim številom prirejena objekta, ki imata to lastnost, da sta večja (oziroma manjša) od vsakega realnega števila.
To sta lahko naprimer kar Zemlja in Sonce. Eden za -inf, drug za +inf.
Potem so pa kardinalna števila števnih (neskončnih!) in neštevnih (nekončnih, ampak še večjih) množic.
Potem so pa še ordinalna števila števila neskončnih množic.
Potem so pa še transalefska števila. Potem so pa še transkonstruktibilna števila.
V resnici, gre za neke ideje, ki ena-ena korespondirajo s stanji človeških možganov. Ali papirja (ekrana), na katerem je to definirano.
To sta lahko naprimer kar Zemlja in Sonce. Eden za -inf, drug za +inf.
Potem so pa kardinalna števila števnih (neskončnih!) in neštevnih (nekončnih, ampak še večjih) množic.
Potem so pa še ordinalna števila števila neskončnih množic.
Potem so pa še transalefska števila. Potem so pa še transkonstruktibilna števila.
V resnici, gre za neke ideje, ki ena-ena korespondirajo s stanji človeških možganov. Ali papirja (ekrana), na katerem je to definirano.
Man muss immer generalisieren - Carl Jacobi
SavoKovac ::
Res imamo več neskončnosti...
Moč nekaterih množič je števno neskončno (aleph zero), nekaterih drugih pa neštevno neskončno.
Moč množice naravnih števil je števno neskončna (prav tako kot moč množice sodih, lihih, raconalnih števil...)
Neštevno neskončno moč imajo npr. množica realnih števil ali pa katerikoli realni interval, ki ima različni meji (npr. (a,b); a,b € |R, a < b). Dokaže se tudi lahko, da je ima interval (0,1) enako št. elementov kot pa sama množica realnih števil.
Moč nekaterih množič je števno neskončno (aleph zero), nekaterih drugih pa neštevno neskončno.
Moč množice naravnih števil je števno neskončna (prav tako kot moč množice sodih, lihih, raconalnih števil...)
Neštevno neskončno moč imajo npr. množica realnih števil ali pa katerikoli realni interval, ki ima različni meji (npr. (a,b); a,b € |R, a < b). Dokaže se tudi lahko, da je ima interval (0,1) enako št. elementov kot pa sama množica realnih števil.
Rokec ::
Sam če daljico neskončnokrat presekaš na pol, dobiš daljico dolžine 0 (v limiti, seveda), kar je točka!
Krog je pa še vedno krog, le da je neskončno velik! Sej kaj pa če pri normalno velikem krogu gledaš ukrivljenost na neskončno majhnem koščku?!
Krog je pa še vedno krog, le da je neskončno velik! Sej kaj pa če pri normalno velikem krogu gledaš ukrivljenost na neskončno majhnem koščku?!
Thomas ::
"Neskončno majhni končki", takoimenovani "infinitezmali", so že četrta varianta neskončnosti. Ki pa so že odšli na smetišče, vendar so jih potem spet oživili nekateri matematični teoretiki.
Še en snapshot ali movie iz človeških možganov pa ustreza temu.
Še en snapshot ali movie iz človeških možganov pa ustreza temu.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Za vsak aksiomatski sistem, za dokazovanje vsakega izreka v njem, obstaja 4D nevronski "žurnal". 
Man muss immer generalisieren - Carl Jacobi
antonija ::
A ni poanta limite da tega ni? Ce ena funkcija limitira proti nic, potem to pomeni da se bliza tej vrednosti ko gre proti neskoncnosti. Nam ni noben reku da res kdaj doseze limitno vrednost... Torej je tist krog se zmeri cist lep krog, ker koeficient ukrivljenosti ni nic amapk se samo bliza nicli z vecanjem radija. Nikoli ni nic. In tista daljica je se zmeraj daljica, ker pomojem noben tle ne ve kolk je velka tocka. (baje da je nic po vseh dimenzijah, sam vseen) Pa ce mas nekaj kar ima dolzino (recimo daljico) in to dajes na pol pol sploh ni variante da prides do dolzine nic. Dobis sicer zeloooo majhno daljico, ampak to je tudi vse. Nikoli ni nic.
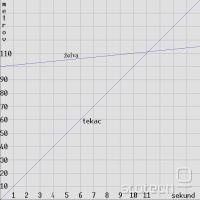
To me najbolj spomn na neskoncne vrste... Prvi mesec na faksu nam je profesor povedal zgodbico o zelvi in sprinterju ki sta tekmovala. Zelva je imela 100m prednosti! Tekac tece s hitrostjo 10m/s, zelva pa borih 1m/s. Ko tekac pretece 100m do zelve (10s), mu ta pobegne za 10m. Ko pretece 10m, mu zelva pobegne za 1m...... zadevo se seveda da delat v neskoncnost in tko bi se se komu zazdelo da ta bogi tekac nebo nikoli prhitu tiste zelve... Ampak vsak ve da jo. Pr tej enskoncnosti je neki tko nerealnega da se je ne da predstavit z realnimi stvarmi (krog, daljica)... Vsaj mene zmeri neki bega pri teh poskusih uresnicenja neskoncnosti.
Tekac tece s hitrostjo 10m/s, zelva pa borih 1m/s. Ko tekac pretece 100m do zelve (10s), mu ta pobegne za 10m. Ko pretece 10m, mu zelva pobegne za 1m...... zadevo se seveda da delat v neskoncnost in tko bi se se komu zazdelo da ta bogi tekac nebo nikoli prhitu tiste zelve... Ampak vsak ve da jo. Pr tej enskoncnosti je neki tko nerealnega da se je ne da predstavit z realnimi stvarmi (krog, daljica)... Vsaj mene zmeri neki bega pri teh poskusih uresnicenja neskoncnosti.
To me najbolj spomn na neskoncne vrste... Prvi mesec na faksu nam je profesor povedal zgodbico o zelvi in sprinterju ki sta tekmovala. Zelva je imela 100m prednosti!
Statistically 3 out of 4 involved usually enjoy gang-bang experience.
ThePlayer ::
Matematika v prvem smislu ne opisuje narave, le abstraktne modele. Obstajajo pa matematični objekti, ki jih "po čudežu" najdemo tudi v naravi. Recimo zlati rez, čebele vedo zakaj je treba delat panj v obliki šestkotnikov,... skratka zabavni del matematike. Z drugim se niti ni treba obremenjevat, če matematike ne študiraš. Rajš se drž programiranja, je bolj "zemeljsko".
Po moje je pa narava osnova za matematiko. Vsaj temeljni aksiomi morajo izhajati iz narave, drugače bi bila matematika neuporabna, a ni tko? Mislim da je matematika v osnovi kup ugotovitev, ki jih je človek pridobil iz opazovanja narave in jih nato posplošil (upoštevaje vse dotedanje ugotovitve).
Glede te želve pa mislim da gre tukaj predvsem za napačno obravnavanje problema.
Po moje je pa narava osnova za matematiko. Vsaj temeljni aksiomi morajo izhajati iz narave, drugače bi bila matematika neuporabna, a ni tko? Mislim da je matematika v osnovi kup ugotovitev, ki jih je človek pridobil iz opazovanja narave in jih nato posplošil (upoštevaje vse dotedanje ugotovitve).
Glede te želve pa mislim da gre tukaj predvsem za napačno obravnavanje problema.
antonija ::
Mtematika opisuje abstarktne modele. Ce se jim narava dovolj pribliza potem opisuje tudi naravo. In na sreco se to dostikrat nardi. Je pa matematika dogovor.
Matematika je zlo stara veda, in ko so jo zacel gruntat so jo apliciral na abstrakne probleme s kerimi so pol probal resit relane probleme. Ene sorte simulacija pac, samo da ni na kompjuterju ampak v glavi. Tko kot vsak problem ki ga resujemo. Nardimo v glavi simulacijo in ce tam dela pol probamo. Ce zajebemo gremo se enkrat znova z novimi podatki...
Glede zelve gre pa za problem neskoncnih vrst. Tud ce so neskoncne (neskonsno veliko clenov) majo lahko vsoto. In vrsta z zelvo in tekacem jo ima. In verjetno bi vsak, ki je ze resil nalogo tipa "kje se zaletita vlaka", znal resiti to nalogo na drugacen nacin. Vrsta je pa se vedno neskoncna...
Matematika je zlo stara veda, in ko so jo zacel gruntat so jo apliciral na abstrakne probleme s kerimi so pol probal resit relane probleme. Ene sorte simulacija pac, samo da ni na kompjuterju ampak v glavi. Tko kot vsak problem ki ga resujemo. Nardimo v glavi simulacijo in ce tam dela pol probamo. Ce zajebemo gremo se enkrat znova z novimi podatki...
Glede zelve gre pa za problem neskoncnih vrst. Tud ce so neskoncne (neskonsno veliko clenov) majo lahko vsoto. In vrsta z zelvo in tekacem jo ima. In verjetno bi vsak, ki je ze resil nalogo tipa "kje se zaletita vlaka", znal resiti to nalogo na drugacen nacin. Vrsta je pa se vedno neskoncna...
Statistically 3 out of 4 involved usually enjoy gang-bang experience.
Zgodovina sprememb…
- spremenilo: antonija ()
fogl ::
Enkrat nam je profesor na faksu povedal: če imaš neskončno klopi v vrsti, in če šteješ samo vsako ta drugo, drugič pa samo vsako ta tretjo, potem pa primerjaš katerih je več...katerih? Enako jih je-v obeh primerih neskončno....zanimivo 
lp, klemen
snow ::
Sem čisto zadovoljen z nekje desetino velikosti elektrona navzdol ter velikostjo vesolja navzgor. 
Random mutation plus nonrandom cumulative natural selection - Richard Dawkins
pramarko ::
>> A ni poanta limite da tega ni? Ce ena funkcija limitira proti nic, potem to pomeni da se bliza tej vrednosti ko gre proti neskoncnosti. Nam ni noben reku da res kdaj doseze limitno vrednost...
Poenostavljeno rečeno uporabljamo limite, kadar nečesa ne moremo direkt zračunat - ne moremo narediti enačaja. Če odmislim, da so limite zelo uporabne, se mi zdi, da so nekakšen bypass za primere, kjer matematiki sicer zagusti. Ja, dejansko limitne vrednosti naj ne bi nikoli dosegli, ampak to se mi zdi le nekakšna varovalka, saj bi sicer katero izmed osnovnih pravil matematike ne držalo (npr: ne smemo deliti z 0). Primer z želvo (btw, ta želva se mi zdi ful hitra :)) je povsem nazoren... tekač je naj ne bi nikoli ujel, pa vemo, da jo. Limitna vrednost naj ne bi nikoli nastopila... pa je to res?
K bodo pogruntali bugfix za tole neskončnost, se bomo (oz. bodo naši zanamci) najbrž čudili, kako smo lahko tako zmotno razmišljali. Ta šolski sistem, ki samo sili učence shranjevati večje in večje količine podatkov, na drugi strani pa bolj malo prispeva k inovativnosti, ali jo celo zatira, je ZASTAREL! Starogrški sistem je bil najbrž bolj učinkovit, vendar si ne znam predstavljat, kako bi ga aplicirali v današnji čas.
Poenostavljeno rečeno uporabljamo limite, kadar nečesa ne moremo direkt zračunat - ne moremo narediti enačaja. Če odmislim, da so limite zelo uporabne, se mi zdi, da so nekakšen bypass za primere, kjer matematiki sicer zagusti. Ja, dejansko limitne vrednosti naj ne bi nikoli dosegli, ampak to se mi zdi le nekakšna varovalka, saj bi sicer katero izmed osnovnih pravil matematike ne držalo (npr: ne smemo deliti z 0). Primer z želvo (btw, ta želva se mi zdi ful hitra :)) je povsem nazoren... tekač je naj ne bi nikoli ujel, pa vemo, da jo. Limitna vrednost naj ne bi nikoli nastopila... pa je to res?
K bodo pogruntali bugfix za tole neskončnost, se bomo (oz. bodo naši zanamci) najbrž čudili, kako smo lahko tako zmotno razmišljali. Ta šolski sistem, ki samo sili učence shranjevati večje in večje količine podatkov, na drugi strani pa bolj malo prispeva k inovativnosti, ali jo celo zatira, je ZASTAREL! Starogrški sistem je bil najbrž bolj učinkovit, vendar si ne znam predstavljat, kako bi ga aplicirali v današnji čas.
SavoKovac ::
Starogrški sistem je res zanimiv...vendar si ga ne želet nazaj...
Brez arabskih števil, teorije množic, odvodov, integralov, kompleksnih števil... si naprimer danes sodobne fizike sploh ne da predstavljati (diferencialne enačbe...)
Brez sodobne fizike pa tudi računalništva ne bi bilo takšnega, kot ga poznamo in tudi na tem forumu zdaj ne bi mogli tako razpravljati.
Brez arabskih števil, teorije množic, odvodov, integralov, kompleksnih števil... si naprimer danes sodobne fizike sploh ne da predstavljati (diferencialne enačbe...)
Brez sodobne fizike pa tudi računalništva ne bi bilo takšnega, kot ga poznamo in tudi na tem forumu zdaj ne bi mogli tako razpravljati.
Thomas ::
Nisem tako prepričan, da je bila tale ideja o zveznosti več, kot pragmatična poenostavitev.
Današnja digitalna (diskretna) matematika, lahko emulira "zvezno". Da ne govorimo o tem, da je zvezna potrebna samo še zato, ker so stari kozli (15+ let) večinoma tako navajeni.
Današnja digitalna (diskretna) matematika, lahko emulira "zvezno". Da ne govorimo o tem, da je zvezna potrebna samo še zato, ker so stari kozli (15+ let) večinoma tako navajeni.
Man muss immer generalisieren - Carl Jacobi
pramarko ::
Če ni neskončnosti... kaj pa potem je? A se v "neskončnih vrednostih" naredi loop v npr. 0 oz. kako drugo vrednosti (pač odvisno od situacije)?
Vsekakor mi je tale ideja, da neskončnosti ni, zelo všeč, čeprav si najbrž ne morem "neneskončnosti" nič bolje predstavljat kakor neskončnost.
Še eno vprašanje, ki se mi zdi povezano z vprašanjem neskončnosti: Kaj je na robu prostor-časa? Ali pa lažje :) vprašanje, kaj je na robu vesolja?
Swashta!
Vsekakor mi je tale ideja, da neskončnosti ni, zelo všeč, čeprav si najbrž ne morem "neneskončnosti" nič bolje predstavljat kakor neskončnost.
Še eno vprašanje, ki se mi zdi povezano z vprašanjem neskončnosti: Kaj je na robu prostor-časa? Ali pa lažje :) vprašanje, kaj je na robu vesolja?
Swashta!
Thomas ::
> kaj pa dogodki pred big bangom
Eternal Past - je že izključena zadeva. Alant Guth. Eternal Future ni čisto izključena.
> ali pa crne luknje ?
Tam ni nič neskončnega. Fizikalna singularnost tako ne obstaja. Vse je v površini črne luknje.
> a je to neskoncnost ?
Seveda ne. Celo Eternal Future lahko živi brez neskončnosti!
Eternal Past - je že izključena zadeva. Alant Guth. Eternal Future ni čisto izključena.
> ali pa crne luknje ?
Tam ni nič neskončnega. Fizikalna singularnost tako ne obstaja. Vse je v površini črne luknje.
> a je to neskoncnost ?
Seveda ne. Celo Eternal Future lahko živi brez neskončnosti!
Man muss immer generalisieren - Carl Jacobi
Thomas ::
> Kaj je na robu prostor-časa?
Roba nima. Kamor lahko prideš, je kaj okoli. Četudi je flat.
Roba nima. Kamor lahko prideš, je kaj okoli. Četudi je flat.
Man muss immer generalisieren - Carl Jacobi
tsd ::
neskončnost kot tudi bog obstajata.
kakšna sta je pa drugo vprašanje.
zaradi naše nepopolnosti si ju predstavljamo iznakaženo.
kakšna sta je pa drugo vprašanje.
zaradi naše nepopolnosti si ju predstavljamo iznakaženo.
CaqKa ::
oni tekač prehiti želvo malo po 11sekundah tak da nevem kaj bluzite z neko želvo.
zadevo se seveda da delat v neskoncnost in tko bi se se komu zazdelo da ta bogi tekac nebo nikoli prhitu tiste zelve...
>>> ne zadeve se ne da delat v neskončnost... če bo to htel tak bi morala oba počasi zniževat svojo hitrost. tak kot je pa zdaj naloga zastavljna pa sta to dve premici z različnim naklonom in ta počasnejša je višje premaknjena.
zadevo se seveda da delat v neskoncnost in tko bi se se komu zazdelo da ta bogi tekac nebo nikoli prhitu tiste zelve...
>>> ne zadeve se ne da delat v neskončnost... če bo to htel tak bi morala oba počasi zniževat svojo hitrost. tak kot je pa zdaj naloga zastavljna pa sta to dve premici z različnim naklonom in ta počasnejša je višje premaknjena.
Zgodovina sprememb…
- spremenil: CaqKa ()
OwcA ::
Poanta Zenonovega paradoksa je v tem, da sprejmeš njegove premise, potem je pa zabavno. 
Otroška radovednost - gonilo napredka.
pramarko ::
>> Roba nima. Kamor lahko prideš, je kaj okoli. Četudi je flat.
Sori, ampak zdi se mi, da ti tule ne sledim. A ti tole svojo zgornjo trditev dejansko tudi razumeš, al si to samo povzel po svojemu idejnemu vodji? Če ima vsako mesto v vesolju tudi svojo okolico, iz tega logično sledi, da je vesolje neskončno... ane??? Pa zraven tudi trdiš, da roba nima. Sploh če je flat in nima robu, bi sklepal, da je torej vesolje neskončno. Drugo bi bilo, če ni plosko.
A je prostor-čas kaj več kot vesolje?
Sori, ampak zdi se mi, da ti tule ne sledim. A ti tole svojo zgornjo trditev dejansko tudi razumeš, al si to samo povzel po svojemu idejnemu vodji? Če ima vsako mesto v vesolju tudi svojo okolico, iz tega logično sledi, da je vesolje neskončno... ane??? Pa zraven tudi trdiš, da roba nima. Sploh če je flat in nima robu, bi sklepal, da je torej vesolje neskončno. Drugo bi bilo, če ni plosko.
A je prostor-čas kaj več kot vesolje?
Valentin ::
Naš prostor-čas je na velikih razdaljah zakrivljen sam vase. Če bi pričel dolgo potovanje skozi vesolje, ves čas v eni smeri, bi nekoč prišel na izhodiščno točko.
Torej tistega 'roba' vesolja ne moreš nikdar doseči.
Torej tistega 'roba' vesolja ne moreš nikdar doseči.
Brane2 ::
Ta primer z zelvo je IMHO eden nazornejsih, ki kazejo na skodljive vplive marihuane na cloveske mozgane. 
Zelva tekacu nikoli ne "uide", le s svojim premikom povečuje preostalo potrebno pot tekaca.
Primer bi mogoce celo lahko veljal, ce bi bila tekac in zelva zelo majhna in ce bi si tekac prizadeval denimo stopiti na zelvo, ne pa jo prehiteti.
Kadarkoli bi naredil tisti zadnji korak, ki bi ga pripeljal na zelvin hrbet, bi se mu t a izmaknila zadosti, da bi jo zgresil...
Zelva tekacu nikoli ne "uide", le s svojim premikom povečuje preostalo potrebno pot tekaca.
Primer bi mogoce celo lahko veljal, ce bi bila tekac in zelva zelo majhna in ce bi si tekac prizadeval denimo stopiti na zelvo, ne pa jo prehiteti.
Kadarkoli bi naredil tisti zadnji korak, ki bi ga pripeljal na zelvin hrbet, bi se mu t a izmaknila zadosti, da bi jo zgresil...
Thomas ::
Finitisti se ne sklicujemo na Zenov paradox pri svojem obračunu z neskončno mistiko.
Zenov paradox je znotraj neskončnega razrešljiv. Namreč, Zeno, če se izraža prav, ne reče, da Ahil nikoli ne dihiti želve, pač pa mora reči, da je ne dohiti po nobenem končnem številu zavzemanja njenega prejšnjega mesta!
Asumpcija, da je to (poboldano) kar isto, ni taprava!
Zdej pa k Vesolju! Pogledaš od kateregakoli delca v vse smeri, pa vidiš, da imaš v vsaki smeri približno enako delcev. Vsota notranjih kotov trikotnika je pa dva prava kota.
Kako je tak prostor sploh možen? Kar mi razumemo kot "ta prostor", je samo emergent property informacijskih procesov, ki so v coreu sveta.
Še par besedic o "duhovnih očetih". Vsak oče (mati) ima ima kvečjemu ene par idej. Moj skromni cilj jih je rekrutirati vse te najsposobnejše "otroke" v eno učinkovito armado. Finitistične ideje so high ranking v tej vojski.
Zenov paradox je znotraj neskončnega razrešljiv. Namreč, Zeno, če se izraža prav, ne reče, da Ahil nikoli ne dihiti želve, pač pa mora reči, da je ne dohiti po nobenem končnem številu zavzemanja njenega prejšnjega mesta!
Asumpcija, da je to (poboldano) kar isto, ni taprava!
Zdej pa k Vesolju! Pogledaš od kateregakoli delca v vse smeri, pa vidiš, da imaš v vsaki smeri približno enako delcev. Vsota notranjih kotov trikotnika je pa dva prava kota.
Kako je tak prostor sploh možen? Kar mi razumemo kot "ta prostor", je samo emergent property informacijskih procesov, ki so v coreu sveta.
Še par besedic o "duhovnih očetih". Vsak oče (mati) ima ima kvečjemu ene par idej. Moj skromni cilj jih je rekrutirati vse te najsposobnejše "otroke" v eno učinkovito armado. Finitistične ideje so high ranking v tej vojski.
Man muss immer generalisieren - Carl Jacobi
nicjasno ::
t.g. : matematika pozna neskoncnost. V naravi je pa ni. Zato je matematicna resitev 1/0 res neskoncno, v naravi pa to ni mozno.
www.nicjasno.com | www.vsejasno.com
Thomas ::
> koliko je potem 1/0?
Zakaj bi pa moralo to kaj biti? Zakaj bi moralo biti ravno "neko število"?
Vsakemu zaporedju besed naj v naravi nekaj ustreza? Ni nujno!
Stavkov je mnogo več, kot je reči. Zato so nekateri stavki prazni pomena. "1/0" je že tak.
Lahko pa definiramo nek objekt, večji od vsakega števila. Edino ne sme biti nobeno število, druge omejitve ni. Lahko je naprimer množica, ki vsebuje vsa pozitivna števila in 0. Naprimer. Zdaj lahko rečemo "1/0=inf".
Zataknilo se bo nekoliko kasneje, ko se bomo vprašali, koliko je inf-inf.
Brezplodno lahko kompliciramo še dalje. Komu na čast? Stari šoli in stari gardi? Jest ne bi.
Zakaj bi pa moralo to kaj biti? Zakaj bi moralo biti ravno "neko število"?
Vsakemu zaporedju besed naj v naravi nekaj ustreza? Ni nujno!
Stavkov je mnogo več, kot je reči. Zato so nekateri stavki prazni pomena. "1/0" je že tak.
Lahko pa definiramo nek objekt, večji od vsakega števila. Edino ne sme biti nobeno število, druge omejitve ni. Lahko je naprimer množica, ki vsebuje vsa pozitivna števila in 0. Naprimer. Zdaj lahko rečemo "1/0=inf".
Zataknilo se bo nekoliko kasneje, ko se bomo vprašali, koliko je inf-inf.
Brezplodno lahko kompliciramo še dalje. Komu na čast? Stari šoli in stari gardi? Jest ne bi.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
> matematika pozna neskoncnost. V naravi je pa ni. Zato je matematicna resitev 1/0 res neskoncno, v naravi pa to ni mozno.
Se strinjam.
Dodal bi samo to, da vsa dosedanja matematika, vse njene konstrukcije, so v resnici popolnoma opisane z vsemi možnimi 4D muviji (3D+time) človeških možganov.
Kaj pa jutrišnja? 4D muviji drugih substratov.
Pojasnilo:
slika - 2D
muvi - 3D (slika v času)
4d muvi - hologram v času.
Vsaka matematika ima neko fiziko odzadaj, ali pa je ni!
Dobr a?
Se strinjam.
Dodal bi samo to, da vsa dosedanja matematika, vse njene konstrukcije, so v resnici popolnoma opisane z vsemi možnimi 4D muviji (3D+time) človeških možganov.
Kaj pa jutrišnja? 4D muviji drugih substratov.
Pojasnilo:
slika - 2D
muvi - 3D (slika v času)
4d muvi - hologram v času.
Vsaka matematika ima neko fiziko odzadaj, ali pa je ni!
Dobr a?
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Se reče, kaj je računanje 5+7=12?
Nek fizikalni proces.
Kaj je dokazovanje, da "sqrt(2)!=a/b za vsak integer par a, b"?
To je nek fizikalni proces. Hologramski movie.
Kaj je Teorija množic? Hologramski movie. S končno resolucijo in končnim številom frameov, ker če drugega ne, energije za predvajanje tega hologramskega muvija zmanjka!
Nek fizikalni proces.
Kaj je dokazovanje, da "sqrt(2)!=a/b za vsak integer par a, b"?
To je nek fizikalni proces. Hologramski movie.
Kaj je Teorija množic? Hologramski movie. S končno resolucijo in končnim številom frameov, ker če drugega ne, energije za predvajanje tega hologramskega muvija zmanjka!
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Ali da povem drugače. Nobene matematike v bistvu ni. So samo s kredo na tablo naneseni sledovi, bliskanje nevronov, preklapljanja tranzistorjev ... temu rečemo matematika. Eni veliki množici holografskih muvijev, smo se odločili reči "matematika". Svet ki ga naj bi opisovala, pa ne obstaja. Obstaja samo svet, kjer se ta imaginarni svet opisuje.
Pravljičar je, Rdeče Kapice pa ni. On samo fabulira.
Pravljičar je, Rdeče Kapice pa ni. On samo fabulira.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Mogoče niste vedeli, ampak najmanjše neskonćno transfinitno število je aleph0.
aleph1=2aleph0.
Pri čemer je aleph0 število naravnih števil. (Pa še ulomkov, celih, praštevil ... in še katerih). aleph1 je pa število realnih števil, meddrugim.
No ja, to ste najbrž vsi vedeli, da naj bi bilo tako.
Kar je manj znano je problem, če naj bi obstajalo neskončno kardinalno število X tako, da bi veljalo:
aleph0 < X < aleph1
To je bilo dolg znano kot problem kontinuuma.
Ko so končno razčistili kako je s tem, so ugotovili (Coehn), da je vseeno, če vzamemo da tak X je, ali pa če vzamemo da ga ni. Celo zelo poljubno mnogo različnih Xov smemo nametati med oba alefa. Ali pa nič. Poljubno.
To meni pomeni samo - zabriši proč še frdamane alefe! Hehehe.
aleph1=2aleph0.
Pri čemer je aleph0 število naravnih števil. (Pa še ulomkov, celih, praštevil ... in še katerih). aleph1 je pa število realnih števil, meddrugim.
No ja, to ste najbrž vsi vedeli, da naj bi bilo tako.
Kar je manj znano je problem, če naj bi obstajalo neskončno kardinalno število X tako, da bi veljalo:
aleph0 < X < aleph1
To je bilo dolg znano kot problem kontinuuma.
Ko so končno razčistili kako je s tem, so ugotovili (Coehn), da je vseeno, če vzamemo da tak X je, ali pa če vzamemo da ga ni. Celo zelo poljubno mnogo različnih Xov smemo nametati med oba alefa. Ali pa nič. Poljubno.
To meni pomeni samo - zabriši proč še frdamane alefe! Hehehe.
Man muss immer generalisieren - Carl Jacobi
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Cantor, Russell ... Teorija množic. (strani: 1 2 3 )Oddelek: Znanost in tehnologija | 11055 (9536) | Odin |
| » | Godlov aksiom neizpeljivosti (strani: 1 2 3 )Oddelek: Znanost in tehnologija | 9954 (7863) | Vesoljc |
| » | abstraktni elementiOddelek: Znanost in tehnologija | 2397 (2026) | Roadkill |
| » | Filozofija ZnanostiOddelek: Znanost in tehnologija | 2535 (2157) | Thomas |
| » | Neskončno... (strani: 1 2 )Oddelek: Loža | 8789 (7703) | Gh0st |