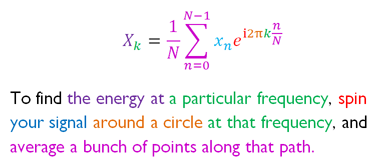Forum » Šola » DFT
DFT
marjan_h ::
marjan_h ::
Ja za povprečje je 1/N. Vendar druge enačbe FT na netu ne računajo povprečje. Pa še minus v eksponentu me moti.
one too many ::
Za minus je vseeno. Brez minusa imaš inverzno transformacijo, torej je to bolj stvar dogovora. Sicer minus učinkuje samo tako, da imaginarni del pomnoži z -1.
Tudi 1/N je dogovor (ki je seveda odvisen od področja do področja). Nekje ima transformacija in inverzna trans. 1/sqrt(N), 1/sqrt(N), ponekod ima pa en 1/N in drugi samo faktor 1.
Zakaj mora biti skupaj faktor 1/N? Zato da dobiš po inverzni transformaciji transformacije originalne podatke.
Tudi 1/N je dogovor (ki je seveda odvisen od področja do področja). Nekje ima transformacija in inverzna trans. 1/sqrt(N), 1/sqrt(N), ponekod ima pa en 1/N in drugi samo faktor 1.
Zakaj mora biti skupaj faktor 1/N? Zato da dobiš po inverzni transformaciji transformacije originalne podatke.
marjan_h ::
Aja, jaz sem pa mislil da je samo enolična definicija FT. Kako to da ni, in kje se uporablja te različne variacije FT?
one too many ::
V bistvu je definicija vedno enaka.
Mislim pa, da je vedno DFT definiran z minusom. Torej pri razlagi gre lahko za inverz, ampak glede na to, da je vsota po n, dvomim. Sicer je pa to internet in napako so možne.
Matematiki imajo ponavadi 1/sqrt(N), praktično vsepovsod drugje pa je po mojih izkušnjah enkrat 1/N. Zakaj, ne vem. Verjetno sprotni faktor 1/sqrt(N) nudi kakšne dodatne lastnosti ali pa je zgolj zaradi simetrije. Enkratni faktor 1/N pa je bolj praktičen.
Npr., v fiziki se pogosto rabi exp(i*E/hbar*t), kjer je E/hbar=omega=2*pi*f. Prehaja se med E in t, ker je E (energija, npr. elektrona v polprevodniku) veliko bolj naravna enota kot frekvenca (ki v bistvu ne pomeni frekvence nihanja...).
Ravno tako imamo exp(i*k*x), kjer je valovni vektor k=2*pi/lambda. Ne vem, če sploh obstaja ekvivalent frekvence k valovni dolžini lambda, temveč samo k.
Spet ker je v kvantni mehaniki direktna povezava med valovno dolžino in gibalno količino: p = hbar*k, se pogosto prehaja med x in p.
Po drugi strani je pri kakšni analizi zvočnega signala frekvenca (2*pi*f) veliko bolj naravna enota kot omega (krožna frekvenca).
Vidiš, da so vse definicije enake, le da enkrat prehajajo med frekvenco in časom, drugič energijo in časom, tretjič med gibalno količino in koordinato(?). In ravno to je smisel (D)FT, prehod med različnimi prostori.
Sam bi sicer poskušal razumeti DFT iz smeri zvezne FT. Najprej si pa poglej Fourierove vrste.
Mislim pa, da je vedno DFT definiran z minusom. Torej pri razlagi gre lahko za inverz, ampak glede na to, da je vsota po n, dvomim. Sicer je pa to internet in napako so možne.
Matematiki imajo ponavadi 1/sqrt(N), praktično vsepovsod drugje pa je po mojih izkušnjah enkrat 1/N. Zakaj, ne vem. Verjetno sprotni faktor 1/sqrt(N) nudi kakšne dodatne lastnosti ali pa je zgolj zaradi simetrije. Enkratni faktor 1/N pa je bolj praktičen.
Npr., v fiziki se pogosto rabi exp(i*E/hbar*t), kjer je E/hbar=omega=2*pi*f. Prehaja se med E in t, ker je E (energija, npr. elektrona v polprevodniku) veliko bolj naravna enota kot frekvenca (ki v bistvu ne pomeni frekvence nihanja...).
Ravno tako imamo exp(i*k*x), kjer je valovni vektor k=2*pi/lambda. Ne vem, če sploh obstaja ekvivalent frekvence k valovni dolžini lambda, temveč samo k.
Spet ker je v kvantni mehaniki direktna povezava med valovno dolžino in gibalno količino: p = hbar*k, se pogosto prehaja med x in p.
Po drugi strani je pri kakšni analizi zvočnega signala frekvenca (2*pi*f) veliko bolj naravna enota kot omega (krožna frekvenca).
Vidiš, da so vse definicije enake, le da enkrat prehajajo med frekvenco in časom, drugič energijo in časom, tretjič med gibalno količino in koordinato(?). In ravno to je smisel (D)FT, prehod med različnimi prostori.
Sam bi sicer poskušal razumeti DFT iz smeri zvezne FT. Najprej si pa poglej Fourierove vrste.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | EnačbaOddelek: Šola | 1078 (938) | lebdim |
| » | PI is wrong! (strani: 1 2 3 4 )Oddelek: Znanost in tehnologija | 19693 (12997) | modicr |
| » | Matematika - FMF (strani: 1 2 )Oddelek: Šola | 11370 (9103) | sherman |
| » | E (matematična konstanta) (strani: 1 2 3 4 )Oddelek: Šola | 17011 (11475) | Jst |
| » | Naloga iz matematične indukcijeOddelek: Šola | 2622 (2271) | Marc` |