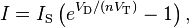Forum » Šola » E (matematična konstanta)
E (matematična konstanta)
micromollis ::
V šoli sem dobil nalogo, da naredim predstavitev matematične konstante e. Na netu sem našel polno literature, ki konstanto na sto in en način opišejo iz matematičnega vidika, nikjer pa nisem našel nobenega članka, ki bi na malo bolj poljudnoznanstveni način predstavil kje zasledimo to število v naravi, kako pridemo do njega iz raznih izračunov ipd. Glede na to, da so na tem forumu sami razgledani matematiki, se njihovih odgovorov nič ne branim 
 .
.
Hvala!
PS: Predvsem upam, da bodo odgovori na nivoju srednje šole 2. letnika in da jih bo zdrava kmečka pamet dojela :)
Hvala!
PS: Predvsem upam, da bodo odgovori na nivoju srednje šole 2. letnika in da jih bo zdrava kmečka pamet dojela :)
micromollis ::
Wiki sem že celo obdelal, vendar uporabnih stvari je v slovenščini malo, v angleščini pa so zame nerazumljive. Tako da če se kdo potrudi in zadevo opiše v slovenščini. Nenazadnje je to ena najpomembnejših konstant v matematiki in v slovenščini še ni niti ene debate na to temo .
.
McHusch ::
ex je lepa funkcija, ker ima odvod in nedoločni integral enak funkciji. Pa še enostavno predstavitev v Taylorju ima, poleg tega pa je ln x integral od 1/x.
leinad ::
McHusch malo 2much za drugi letnik SŠ tole a? V realnem svetu jo gre mogoče opaziti recimo pri razvoju računalniške tehnologije, razvoj gre naprej na tem področju najhitreje od vseh tehnoloških panog kolikor vem, če je čisto eksponenten ne vem, ampak kaj daleč vstran IMO ni.
V realnem svetu jo gre mogoče opaziti recimo pri razvoju računalniške tehnologije, razvoj gre naprej na tem področju najhitreje od vseh tehnoloških panog kolikor vem, če je čisto eksponenten ne vem, ampak kaj daleč vstran IMO ni.
whatever ::
Ja v smislu computinga gre res mogoče razvoj eksponentno, ampak vprašanje ostaja še zmeraj, če se da z dovoljšnjo mero computinga res vse pojasnit. Imho ne.
Veliko jih je notri, še več jih je pa zunaj.
Bilijarde v šole! - Ivan Kramberger
Abnormal behaviour of abnormal brain makes me normal.
Bilijarde v šole! - Ivan Kramberger
Abnormal behaviour of abnormal brain makes me normal.
zdobersek ::
gre za isto konstanto kot v tem primeru?
3.38624244428E+47
Lp
edit: typo
3.38624244428E+47
Lp
edit: typo
Zgodovina sprememb…
- spremenil: zdobersek ()
WiseBear ::
Vsi ti formalni matematični zapisi seveda zaživijo v povsem banalnih naravnih procesih. V naravoslovju je tako ogromno količin ki se eksponentno spreminjajo. Nima smisla naštevat, ker jih pravzaprav najdeš povsod...
Če prav hočeš: v kemiji koncentracija reaktantov pri veliko reakcijah eksponentno pada s časom; naravni razpad radioaktivnih jeder se sklada z eksponentno funkcijo, če poljubno snov redčiš s čistim topilom koncentracija te snovi pada eksponentno.....itd
LP
Če prav hočeš: v kemiji koncentracija reaktantov pri veliko reakcijah eksponentno pada s časom; naravni razpad radioaktivnih jeder se sklada z eksponentno funkcijo, če poljubno snov redčiš s čistim topilom koncentracija te snovi pada eksponentno.....itd
LP
Thomas ::
Kje x-ti koren iz x največji?
Pri e. Prej in kasneje je manjši.
Pri e. Prej in kasneje je manjši.
Man muss immer generalisieren - Carl Jacobi
A. Smith ::
S funkcijo e^x opisujemo polnjenje in praznjenje kondenzatorja, segrevanje in ohlajanje homogenega telesa, ter rast populacije ob neomejenih virih.
Kot je na Wikipediji pojasnjeno, je matematik Jacob Bernoulli konstanto e odkril, ko se je ukvarjal s problemom obrestno-obrestnega računa. Obresti izračunamo tako, da v vsakem koraku glavnici najprej prištejemo stare obresti.
(sledi prevod članka - rotKapica, boš dal za pijačo)
Če imamo torej na banki račun z letnim donosom 100%, na njem pa 1€, obresti pa prištevamo 1x letno, dobimo ob koncu leta na računu 2€.
Če obresti prištevamo 2x na leto, nam vrednost na računu v prvi polovici leta zraste na 1,5€ , v drugi polovici leta pa na 1'5 * 1'5 * 1€ = 2,25€
Če obresti prištevamo 4x na leto, dobimo (1,25^4) * 1€ = 2.4414…€
Ob mesečnem prištevanju dobimo 2.613035…€
Bernoulli je pri tem opazil, da se zaporedje z vedno manjšimi intervali bliža limiti. Tedensko prištevanje obresti nam vrne 2.692597…€, dnevno prištevanje pa 2.714567…€, komaj dva centa več.
Če število prištevanj na leto zapišemo s simbolom n, dobimo za n=neskončno izraz
katerega rezultat je konstanta e.
Če bi obresti prištevali skozi celo leto neprekinjeno, bi se na računu pojavila vsota 2.7182818…€. Oziroma splošneje: na računu z 1€ in obrestjo R bomo ob nepretrganem prištevanju obresti dobili vsoto e^R.
Kot je na Wikipediji pojasnjeno, je matematik Jacob Bernoulli konstanto e odkril, ko se je ukvarjal s problemom obrestno-obrestnega računa. Obresti izračunamo tako, da v vsakem koraku glavnici najprej prištejemo stare obresti.
(sledi prevod članka - rotKapica, boš dal za pijačo)
Če imamo torej na banki račun z letnim donosom 100%, na njem pa 1€, obresti pa prištevamo 1x letno, dobimo ob koncu leta na računu 2€.
Če obresti prištevamo 2x na leto, nam vrednost na računu v prvi polovici leta zraste na 1,5€ , v drugi polovici leta pa na 1'5 * 1'5 * 1€ = 2,25€
Če obresti prištevamo 4x na leto, dobimo (1,25^4) * 1€ = 2.4414…€
Ob mesečnem prištevanju dobimo 2.613035…€
Bernoulli je pri tem opazil, da se zaporedje z vedno manjšimi intervali bliža limiti. Tedensko prištevanje obresti nam vrne 2.692597…€, dnevno prištevanje pa 2.714567…€, komaj dva centa več.
Če število prištevanj na leto zapišemo s simbolom n, dobimo za n=neskončno izraz
katerega rezultat je konstanta e.
Če bi obresti prištevali skozi celo leto neprekinjeno, bi se na računu pojavila vsota 2.7182818…€. Oziroma splošneje: na računu z 1€ in obrestjo R bomo ob nepretrganem prištevanju obresti dobili vsoto e^R.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
micromollis ::
Wow, respect. Najlepša hvala vsem za odgovore. Smith, lahko častim pijačo ni problema  .
.
Zelo zanimiv mi je odgovor od Thomasa. Če mogoče še veš za kako tako finto, se toplo priporočam.
Lp
PS: Da ne bo koga zmedlo; spremenil sem si username na micromollis.
Zelo zanimiv mi je odgovor od Thomasa. Če mogoče še veš za kako tako finto, se toplo priporočam.
Lp
PS: Da ne bo koga zmedlo; spremenil sem si username na micromollis.
Thomas ::
Tale:
e^(pi*Sqrt(-1)) = -1
... ti bo sploh všeč. Pi je seveda uni pi = 3,1415...
e^(pi*Sqrt(-1)) = -1
... ti bo sploh všeč. Pi je seveda uni pi = 3,1415...
Man muss immer generalisieren - Carl Jacobi
micromollis ::
Zanimivo. Čeprav mi ni jasno kako je lahko rezultat izraza e^(pi*Sqrt(-1)) realno število in ne kompleksno. Predpostavljam, da je to tudi razlog, zakaj si napisal ta primer.
Lp
Lp
Zgodovina sprememb…
- spremenilo: micromollis ()
kekz ::
Če imamo torej na banki račun z letnim donosom 100%,...
Eh, tale primer je napačen. Bolje rečeno slabo izbran za tole tematiko.
Tako so včasih naše banke računale obresti, pa so varčevalci hitro skužili, da se najbolj splača vezati 12x po 1 mesec namesto 1x za celo leto ali 2x po pol leta, čeprav so banke prikazovale letno obrestno mero največjo pri vezavi na 1 leto. Izračun je bil pač napačen, tako kot v tem primeru.
Potem so bili zelo pametni in so uvedli "korekcijski faktor", ki je obrestno mero "popravil na pravo vrednost", da so lahko linearno obrestovali (ker je bilo drugače očitno pretrd oreh).
Če je LETNI donos 100%, je pač 100%.
To pomeni, če obresti izplačuješ 2x na leto, da jih ne smeš izplačevati po 50% (linearna stopnja), ampak (v procentih) 100*(sqrt(2)-1), kar znese ~41,5%.
Če jih izplačuješ 4x na leto, vsakič izplačaš obresti 100*(četrti koren(1+p)-1), kar je približno 19% (in ne 25%).
Zgodovina sprememb…
- spremenilo: kekz ()
kekz ::
Je pa res, da običajno po svetu medletne obresti računajo na lažji linearen način in se pri npr. 5% obrestni meri to praktično sploh ne pozna, tudi če obresti izplačuješ dnevno (razlika šele na 6. decimalki).
Težava nastane šele pri veliki inflaciji in posledično ogromnih obrestnih stopnjah (kot smo nekdaj doživeli).
Težava nastane šele pri veliki inflaciji in posledično ogromnih obrestnih stopnjah (kot smo nekdaj doživeli).
JanK ::
Zakaj je e^{i\pi} realno stevilo se da videti iz Eulerjeve formule:
e^{i\phi} = \cos \phi + i \sin \phi.
Ce je \phi = \pi, dobis e^{i\pi} = \cos \pi + i \sin \pi = -1 + i * 0 = -1.
Vec o tem na Wikipediji: Complex Number in Eulerjeva formula
BTW, Posebeno lep primer Eulerjeve formula je Eulerjeva identiteta (malo drugace napisana prejsnja enacba):
e^{i\pi}+1=0
V tej identiteti je namrec zbranih 5 osnovnih matematicnih konstant, pa se tri osnovne matematicne operacije.
e^{i\phi} = \cos \phi + i \sin \phi.
Ce je \phi = \pi, dobis e^{i\pi} = \cos \pi + i \sin \pi = -1 + i * 0 = -1.
Vec o tem na Wikipediji: Complex Number in Eulerjeva formula
BTW, Posebeno lep primer Eulerjeve formula je Eulerjeva identiteta (malo drugace napisana prejsnja enacba):
e^{i\pi}+1=0
V tej identiteti je namrec zbranih 5 osnovnih matematicnih konstant, pa se tri osnovne matematicne operacije.
A. Smith ::
>>>Če je LETNI donos 100%, je pač 100%....
Se pravi, matematična izpeljava konstante e je kul, v bančništvu je pa ni za uporabljat. Zanimivo branje.
EDIT:
Tule pravijo, da gre pri Bernoullijevi izpeljavi za nominalno, pri tvoji pa za efektivno obrestno mero.
Je pa jasno, da ekonomisti uporabljajo slednjo.
Se pravi, matematična izpeljava konstante e je kul, v bančništvu je pa ni za uporabljat. Zanimivo branje.
EDIT:
Tule pravijo, da gre pri Bernoullijevi izpeljavi za nominalno, pri tvoji pa za efektivno obrestno mero.
Je pa jasno, da ekonomisti uporabljajo slednjo.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
Zgodovina sprememb…
- spremenil: A. Smith ()
micromollis ::
A. Smith povezava ne deluje. Nimam dovoljenja za ogled strani => Samo za registrirane člane
Thomas ::
Koliko števil je treba v povprečju random vzeti iz intervala (0,1), da njihova vsota preseže 1?
Jasno, e.
Jasno, e.
Man muss immer generalisieren - Carl Jacobi
A. Smith ::
Wiki - obrestno obrestni račun
Lej, micromollis, kekz je povedal samo, da se v banki dejansko uporablja drugačna metoda za računanje obresti.
Tista Bernoullijeva izpeljava je zgolj izpeljava za konstanto E.
Lej, micromollis, kekz je povedal samo, da se v banki dejansko uporablja drugačna metoda za računanje obresti.
Tista Bernoullijeva izpeljava je zgolj izpeljava za konstanto E.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
Thomas ::
Graf funkcije f(x)=ex je poleg premice EDINA krivulja, ki enako zgleda, ne glede na to, kako oddaljeni smo od ravnine, na kateri je narisana.
Krog recimo je manjši, čim od dlje ga gledamo. Parabola je bolj zaprta, dlje kot smo. Daljica se krajša, ko se oddaljujemo ...
Premica in f(x)=ex pa zgledata iz vsake razdalje enako.
Krog recimo je manjši, čim od dlje ga gledamo. Parabola je bolj zaprta, dlje kot smo. Daljica se krajša, ko se oddaljujemo ...
Premica in f(x)=ex pa zgledata iz vsake razdalje enako.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Ta se spreminja, ko se približuješ ravnini. Iz tega lahko celo sklepaš, ali se približuješ ali oddaljuješ, če poznaš formulo narisane krace.
Kar pa edinole pri premici in eksponentnici ne deluje.
Kar pa edinole pri premici in eksponentnici ne deluje.
Man muss immer generalisieren - Carl Jacobi
JanK ::
Thomas, lahko malo bolj razlozis (pokazes - matematicno) kako je krivulja enaka? Na hitro sem namrec spacal dva grafa in . Edina razlika je skala (spodnji graf je 2x zoomiran), krivulji pa ne izgledata enako. Si mogoce narobe predstavljam kaj si mislil z "izgledata enako"?
Zgodovina sprememb…
- spremenil: JanK ()
JanK ::
Hehe, nisi prav natancno prebral teme, kaj ne :)
Ja, vem, da je krivulja ista, y=e^x. Poanta je ravno v tem, da je PMSM "izgled" odvisen od skale, Thomas pa pravi, da ni. Za premico (skozi izhodisce) se strinjam, da je izgled neodvisen skale.
Ja, vem, da je krivulja ista, y=e^x. Poanta je ravno v tem, da je PMSM "izgled" odvisen od skale, Thomas pa pravi, da ni. Za premico (skozi izhodisce) se strinjam, da je izgled neodvisen skale.
Thomas ::
Ne, nikjer nisem rekel, da vidiš kakšen koordinatni sistem. To bi bila dodatna informacija, ki je jaz nisem vpeljal.
Man muss immer generalisieren - Carl Jacobi
kekz ::
Jaz tudi mislim, da ne drži.
Pri oddaljevanju ali približevanju ravnini, se v vidnem zornem kotu krivulja spreminja, saj se pri oddaljevanju velikost vidnega dela ravnine veča (tisti, ki jo zorni kot zajame), pri približevanju pa manjša.
Krivulja y=e^x pa ima strmino odvisno od pozicije (nalašč ne bom rekel od koordinat).
Torej, če s pogledom zajamemo večji del ravnine (zorni kot pri večji oddaljenosti), je krivulja bolj kriva (vidimo večjo množico strmin).
Če s pogledom zajamemo manjši del ravnine (zorni kot pri manjši oddaljenosti), je krivulja bolj ravna (vidimo manjšo množico strmin).
Zdi se mi celo, da bi splošno veljalo, da vsako zvezno krivuljo v "neskončni bližini" (=takrat, ko imamo zorni kot komaj malo večji kot za eno točko) lahko smatramo kot ravno daljico.
Pri katerikoli premici pa je videz dejansko neodvisen od dela ravnine, ki jo zorni kot omejuje. Vedno je "enako dolga" (= preko celega vidnega polja) in "enako ravna".
Pri oddaljevanju ali približevanju ravnini, se v vidnem zornem kotu krivulja spreminja, saj se pri oddaljevanju velikost vidnega dela ravnine veča (tisti, ki jo zorni kot zajame), pri približevanju pa manjša.
Krivulja y=e^x pa ima strmino odvisno od pozicije (nalašč ne bom rekel od koordinat).
Torej, če s pogledom zajamemo večji del ravnine (zorni kot pri večji oddaljenosti), je krivulja bolj kriva (vidimo večjo množico strmin).
Če s pogledom zajamemo manjši del ravnine (zorni kot pri manjši oddaljenosti), je krivulja bolj ravna (vidimo manjšo množico strmin).
Zdi se mi celo, da bi splošno veljalo, da vsako zvezno krivuljo v "neskončni bližini" (=takrat, ko imamo zorni kot komaj malo večji kot za eno točko) lahko smatramo kot ravno daljico.
Pri katerikoli premici pa je videz dejansko neodvisen od dela ravnine, ki jo zorni kot omejuje. Vedno je "enako dolga" (= preko celega vidnega polja) in "enako ravna".
Sergio ::
Ja, samo ce pa ze obstaja linearna transformacija koordinatnega sistema v stilu x' = k * x oziroma y' = k * y, pa da to se vedno drzi, kar je Thomas rekel, je to se vedno nekaj, kar bi matematiki rekli, da je "lepo".
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
Thomas ::
> Krivulja y=e^x pa ima strmino odvisno od pozicije
Odvod od e^x (strmina) je ... e^x. Eksponentnica se prikaže enaka pod mikroskopom in s prostim očesom. Premica enako.
Krog se poveča, kvadratna mreža tudi, pod mikroskopom.
Odvod od e^x (strmina) je ... e^x. Eksponentnica se prikaže enaka pod mikroskopom in s prostim očesom. Premica enako.
Krog se poveča, kvadratna mreža tudi, pod mikroskopom.
Man muss immer generalisieren - Carl Jacobi
euler ::
Da ne bo nesporazumov:
Graf e^x je od blizu videti kot premica, od daleč pa kot narobe obrnjena črka L. Torej daleč od tega, da bi bila iz poljubne razdalje videti enaka.
Graf e^x je od blizu videti kot premica, od daleč pa kot narobe obrnjena črka L. Torej daleč od tega, da bi bila iz poljubne razdalje videti enaka.
euler ::
Je pa res, da je graf videti enak, če se pomaknemo v levo ali desno, le raztegne se v navpični smeri. Ampak to velja tudi za poljubno eksponentno funkcijo a^x. Pri pomiku za d v desno se graf raztegne s koeficientom a^d v navpični smeri.
whatever ::
U madona, samega Eulerja mamo na forumu. Zgleda, da je vstal iz groba.
Veliko jih je notri, še več jih je pa zunaj.
Bilijarde v šole! - Ivan Kramberger
Abnormal behaviour of abnormal brain makes me normal.
Bilijarde v šole! - Ivan Kramberger
Abnormal behaviour of abnormal brain makes me normal.
Thomas ::
Hja, skoraj dobro razume zadevo. Ne pa čisto.
Pri a^x, če e!=a, ti oddaljevanje/približevanje da informacijo. To je bil moj point.
Pri a^x, če e!=a, ti oddaljevanje/približevanje da informacijo. To je bil moj point.
Man muss immer generalisieren - Carl Jacobi
euler ::
Euler osebno vam sporočam:
Če e^x pogledamo bolj od blizu (to je ekvivalentno transformaciji KS x'=kx in y'=ky), je nova krivulja manj strma. Tudi če dovolimo translacije KS (torej koordinatni osi pozabimo), kar pomeni x'=kx+a, y'=ky+b, še vedno ne dobimo iste krivulje. Pač pa dobimo isto krivuljo če naredimo transformacijo x'=x+a in y'=y*e^a, ampak to NI isto kot pogled od blizu/daleč.
Če e^x pogledamo bolj od blizu (to je ekvivalentno transformaciji KS x'=kx in y'=ky), je nova krivulja manj strma. Tudi če dovolimo translacije KS (torej koordinatni osi pozabimo), kar pomeni x'=kx+a, y'=ky+b, še vedno ne dobimo iste krivulje. Pač pa dobimo isto krivuljo če naredimo transformacijo x'=x+a in y'=y*e^a, ampak to NI isto kot pogled od blizu/daleč.
Thomas ::
> Če e^x pogledamo bolj od blizu (to je ekvivalentno transformaciji KS x'=kx in y'=ky), je nova krivulja manj strma.
Strma je v točki x toliko, kolikor je tam njen odvod. Njen odvod je pa tam e^x.
Ker nimaš podatka, koliko x je, ker ne vidiš koordinatnega sistema, ni nobena točka posebej odlikovana. Enako reč vidiš s 1000 km in 100000000 km.
Strma je v točki x toliko, kolikor je tam njen odvod. Njen odvod je pa tam e^x.
Ker nimaš podatka, koliko x je, ker ne vidiš koordinatnega sistema, ni nobena točka posebej odlikovana. Enako reč vidiš s 1000 km in 100000000 km.
Man muss immer generalisieren - Carl Jacobi
euler ::
Strma je v točki x toliko, kolikor je tam njen odvod. Njen odvod je pa tam e^x.
Bolj ko berem, manj razumem. Če ima e^x, kot praviš, neko lepo lastnost, potem se to lastnost da napisati v obliki enačbe.
Kako se ta enačba glasi?
Thomas ::
Zoomanje funkcije e^x in zoomanje premice ne spremeni slike.
To razumeš?
To razumeš?
Man muss immer generalisieren - Carl Jacobi
whatever ::
Zveni logično, ampak nekaj me bega...
Odvod od funkcije y=e^x je y'=e^x, zato se pokaže enako tudi na diferencialno majhnem odseku.
Recimo, da imamo funkcijo y=kx, torej premico. Potem je njen odvod y'=k. Zakaj jo potem pod mikroskopom vidimo kot premico, ne pa kot ravne (navpične) črte (pri x=k), če je njen odvod konstanta. Potem bi po tej logiki moral bit odvod premice y'=kx, ne pa y'=k.
Odvod od funkcije y=e^x je y'=e^x, zato se pokaže enako tudi na diferencialno majhnem odseku.
Recimo, da imamo funkcijo y=kx, torej premico. Potem je njen odvod y'=k. Zakaj jo potem pod mikroskopom vidimo kot premico, ne pa kot ravne (navpične) črte (pri x=k), če je njen odvod konstanta. Potem bi po tej logiki moral bit odvod premice y'=kx, ne pa y'=k.
Veliko jih je notri, še več jih je pa zunaj.
Bilijarde v šole! - Ivan Kramberger
Abnormal behaviour of abnormal brain makes me normal.
Bilijarde v šole! - Ivan Kramberger
Abnormal behaviour of abnormal brain makes me normal.
Zgodovina sprememb…
- spremenilo: whatever ()
euler ::
Razumem, strinjam se pa ne. Poglej graf iz razdalje 10000000 km in boš videl, da je zelo "oglat", v bližini x=0 je vogal. Če pa se približuješ, pa se vogal gladi.
euler ::
Vidiš, točno, na vogale pa nisem pomislil!
Na enega definitivno ne.
Zoomanje funkcije e^x in zoomanje premice ne spremeni slike.
Zoomanje je EKVIVALENTNO transformaciji y'=ky+b, x'=kx+a. Graf premice je npr. invarianten (se ne spremeni) glede na te transformacije, medtem ko graf e^x ni.
Thomas, ali si že slišal za fraktale? To so strukture, ki so videti enake, ne glede na to, kako od blizu jih pogledaš. Premica npr. je fraktal, medtem ko e^x ni.
A. Smith ::
Thomas me je pri tem spomnil na še eno "modrost", ki so nam jo zaupali v srednji šoli, na faksu smo jo pa po hitrem postopku ovrgli, namreč KOLENO DIODE.
Kolenska napetost diode je napetost, ki ostane na njej. Takole:
Seveda pa je enačba eksponentna;
In zdaj problem: ako ima lahko karakteristika "koleno", če je pa eksponentna?
Tri slike e^x, različno zoomirane:
Zdaj si pa oglejte "kolenske vrednosti" - vsaka drugačna. Naj bo torej uradno - koleno ne obstaja!
No, v praksi se pojem kolena vseeno uporablja. Dioda, ki zdrži 6A, se ponavadi uporablja pri nekaj amperih, ne pa v področju mikroamperov, torej se med njenim delovanjem napetostni padec na njej ne bo pretirano spreminjal.
Teoretikom pa kolenske napetosti ni prav preveč za omenjat.
Kolenska napetost diode je napetost, ki ostane na njej. Takole:
Seveda pa je enačba eksponentna;
In zdaj problem: ako ima lahko karakteristika "koleno", če je pa eksponentna?
Tri slike e^x, različno zoomirane:
Zdaj si pa oglejte "kolenske vrednosti" - vsaka drugačna. Naj bo torej uradno - koleno ne obstaja!
No, v praksi se pojem kolena vseeno uporablja. Dioda, ki zdrži 6A, se ponavadi uporablja pri nekaj amperih, ne pa v področju mikroamperov, torej se med njenim delovanjem napetostni padec na njej ne bo pretirano spreminjal.
Teoretikom pa kolenske napetosti ni prav preveč za omenjat.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
kekz ::
Teoretikom pa kolenske napetosti ni prav preveč za omenjat.
Tole si ti mnogo pretiraval z spreminjanjem vrednosti na Y osi.
Če pogledaš s praktičnega vidika se koleno na X osi ni praktično spremenilo NIČ.
Kaj pa je sprememba s 5 na 50, ko se ti druga (odvisna) vrednost spremeni za 10^n krat.
Če imaš npr. Y v mA, so na prvem grafu čisto praktične vrednosti, že na drugem pa take, da najbrž v vsem vesolju skupaj ni toliko električnega toka.
Na tretjem pa povsem nerealne številke, ki v realnem svetu sploh nimajo pomena v prav nobeni fizikalni količini.
A. Smith ::
>>>Kaj pa je sprememba s 5 na 50, ko se ti druga (odvisna) vrednost spremeni za 10^n krat.
Kolenska napetost, 100mV < U < 700mV
Vrednosti med uA in A so v elektroniki pogoste.
Za primere iz prakse sem pa že povedal, da so diode večinoma uporabljane v območju, kjer je Uk približno konstantna (ali pa nas zanima samo njena max. vrednost) in se pojem lahko uporablja.
Kolenska napetost, 100mV < U < 700mV
Vrednosti med uA in A so v elektroniki pogoste.
Za primere iz prakse sem pa že povedal, da so diode večinoma uporabljane v območju, kjer je Uk približno konstantna (ali pa nas zanima samo njena max. vrednost) in se pojem lahko uporablja.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
Zgodovina sprememb…
- spremenil: A. Smith ()
kekz ::
Vrednosti med uA in A so v elektroniki pogoste.
Vem, saj sem elektronik
In ta največji uporabni razpon je v praksi 10^4 do 10^5 kratni faktor.
Tvoj prvi graf ima enote 10^3, drugi pa 10^28 (=približno toliko, kot je atomov/molekul v nekaj tonah snovi).
Tu vmes ni še vedno prevelik faktor 28/3 ~ 10^9, ampak gromozanski 28-3 ~ 10^25 kratni faktor.
Na tretjem pa, po mojem mnenju veliko več, kot je atomov (ali katerih drugih delcev) v celem vesolju.
A. Smith ::
No, velikanske razlike v zoomiranju so več ali manj iz "pedagoških razlogov" 
Pač razlika je bolj opazna.
Kar pa še ne pomeni, da je pri manjših razponih y vrednosti neobstoječa.
Pač razlika je bolj opazna.
Kar pa še ne pomeni, da je pri manjših razponih y vrednosti neobstoječa.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
Thomas ::
> Thomas, ali si že slišal za fraktale? To so strukture, ki so videti enake, ne glede na to, kako od blizu jih pogledaš. Premica npr. je fraktal, medtem ko e^x ni.
Kako veš, kje na eksponentnici je točka ki predstavlja e^1 in kje e^0, če nimaš zraven koordinatnega sistema?
Ne veš. Poljubno rešitev obstaja.
YES/NO?
Kako veš, kje na eksponentnici je točka ki predstavlja e^1 in kje e^0, če nimaš zraven koordinatnega sistema?
Ne veš. Poljubno rešitev obstaja.
YES/NO?
Man muss immer generalisieren - Carl Jacobi
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | matematkaOddelek: Šola | 3476 (2455) | lebdim |
| » | Matematično vprašanje (strani: 1 2 )Oddelek: Šola | 12673 (10739) | joze67 |
| » | PI is wrong! (strani: 1 2 3 4 )Oddelek: Znanost in tehnologija | 19818 (13122) | modicr |
| » | Matematika - pomoč (strani: 1 2 3 )Oddelek: Šola | 29933 (26508) | daisy22 |
| » | Genetski algoritemOddelek: Programiranje | 3106 (2682) | rasta |