Matematika - 1. letnik faksa @ Slo-Tech

Forum » Šola »
Matematika - 1. letnik faksa

Matematika - 1. letnik faksa

Bikica195 :: 16. okt 2020, 18:56

Pozdravljeni!
Imam vprašanje in sicer, kako se izračuna (postopek) smerni koeficient pri nalogi:

Dana je funkcija:
f(x) = (x³-1)e^x+1
Naklon dane funkcije v točki x₀ = -1 je k = ________

Hvala vsem za pomoč

I walk. I look. I see. I stop. I photograph.

joze67 :: 16. okt 2020, 19:00

Odvajaš, izračunaš f'(x) za x=-1 (torej, f'(-1)) in to je to.

Bikica195 :: 16. okt 2020, 19:05

Hvala, če se ne motim je odvod od zgornje funkcije = f´(x) = 3x²e^x+1

I walk. I look. I see. I stop. I photograph.

Zgodovina sprememb…

spremenilo: Bikica195 (16. okt 2020 ob 19:08)

bluefish :: 16. okt 2020, 19:12

Motiš se. Oglej si pravilo za odvod produkta.

Bikica195 :: 16. okt 2020, 19:43

Pa res. Torej:
f´(x) = (3x²) * (e^x+1)+ (x³-1)* e^x -->*odvod od e^x+1 = e^x

Kako se potem to nadaljuje :8)

I walk. I look. I see. I stop. I photograph.

Zgodovina sprememb…

spremenilo: Bikica195 (16. okt 2020 ob 19:45)

A110 :: 16. okt 2020, 19:45

ne, odvod od e^(x+1)=e^(x+1)

Bikica195 :: 16. okt 2020, 19:46

A110 je 16. okt 2020 ob 19:45 izjavil:

ne, odvod od e^(x+1)=e^(x+1)

Hvala za opozorilo!

I walk. I look. I see. I stop. I photograph.

Bikica195 :: 17. okt 2020, 11:57

Se potem odvaja tako? --> f(x)=(x³-1)e^x+1 = 3x² * e^x+1 + x³-1 * e^x+1 = KAKO SE TO POTEM NAPREJ PORAČUNA??

I walk. I look. I see. I stop. I photograph.

FrRoSt :: 17. okt 2020, 12:30

Bikica195 je 17. okt 2020 ob 11:57 izjavil:

Se potem odvaja tako? --> f(x)=(x³-1)e^x+1 = 3x² * e^x+1 + x³-1 * e^x+1 = KAKO SE TO POTEM NAPREJ PORAČUNA??

Za + ti manjka oklepaj!

Če iščes odvod v točki x=-1 potem to vrednost vstaviš v odvod enačbe f'(-1)=smerni koeficient v točki x=-1!

Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.

Bikica195 :: 17. okt 2020, 12:52

FrRoSt je 17. okt 2020 ob 12:30 izjavil:

Bikica195 je 17. okt 2020 ob 11:57 izjavil:
Se potem odvaja tako? --> f(x)=(x³-1)e^x+1 = 3x² * e^x+1 + x³-1 * e^x+1 = KAKO SE TO POTEM NAPREJ PORAČUNA??

Za + ti manjka oklepaj!

Če iščes odvod v točki x=-1 potem to vrednost vstaviš v odvod enačbe f'(-1)=smerni koeficient v točki x=-1!

Sem potem na splošno prav odvedla, ali se še kaj nadaljuje?
Glede na moj odvod pride: f(x)= (3*1²)*(e¹⁺¹) + (1³-1)*(e¹⁺¹)= 3*e-2*e KAJ SE ZGODI S TEMI E-ji (priti moram le do nekega števila oz. moram poračunati smerni koeficient).

I walk. I look. I see. I stop. I photograph.

Matevz96 :: 17. okt 2020, 12:55

Nisem preverjal odvoda, e je pač številka, vstavi v kalkulator in boš dobila rezultat za f'(-1)

Drugače pa ti bosta teli dve strani kar precej v pomoč:
https://www.symbolab.com
https://www.wolframalpha.com

#hooldthedoor

MasterTade :: 17. okt 2020, 12:56

Bikica195 je 17. okt 2020 ob 12:52 izjavil:

FrRoSt je 17. okt 2020 ob 12:30 izjavil:
Bikica195 je 17. okt 2020 ob 11:57 izjavil:
Se potem odvaja tako? --> f(x)=(x³-1)e^x+1 = 3x² * e^x+1 + x³-1 * e^x+1 = KAKO SE TO POTEM NAPREJ PORAČUNA??

Za + ti manjka oklepaj!

Če iščes odvod v točki x=-1 potem to vrednost vstaviš v odvod enačbe f'(-1)=smerni koeficient v točki x=-1!

Sem potem na splošno prav odvedla, ali se še kaj nadaljuje?
Glede na moj odvod pride: f(x)= (3*1²)*(e¹⁺¹) + (1³-1)*(e¹⁺¹)= 3*e-2*e KAJ SE ZGODI S TEMI E-ji (priti moram le do nekega števila oz. moram poračunati smerni koeficient).

????

Mors omnia aequat

Aston_11 :: 17. okt 2020, 13:10

-1 na 3 je bil ponavadi -1
x + 1 bi ponavadi nastalo -1 + 1 = 0

itd.

FrRoSt :: 17. okt 2020, 13:19

Bikica195 je 17. okt 2020 ob 12:52 izjavil:

FrRoSt je 17. okt 2020 ob 12:30 izjavil:
Bikica195 je 17. okt 2020 ob 11:57 izjavil:
Se potem odvaja tako? --> f(x)=(x³-1)e^x+1 = 3x² * e^x+1 + x³-1 * e^x+1 = KAKO SE TO POTEM NAPREJ PORAČUNA??

Za + ti manjka oklepaj!

Če iščes odvod v točki x=-1 potem to vrednost vstaviš v odvod enačbe f'(-1)=smerni koeficient v točki x=-1!

Sem potem na splošno prav odvedla, ali se še kaj nadaljuje?
Glede na moj odvod pride: f(x)= (3*1²)*(e¹⁺¹) + (1³-1)*(e¹⁺¹)= 3*e-2*e KAJ SE ZGODI S TEMI E-ji (priti moram le do nekega števila oz. moram poračunati smerni koeficient).

Odvedeno je že prav, lahko bi odvajala tudi kot sestavljeno funkcijo, g(x)=x³-1 in odvajaš po pravilu za odvajanje sestavljenih funkcij.....

Enačbo lahko urediš, lahko greš pa ksr računati, samo moraš PRAVILNO!!! TOČKO zspisati!! X = - 1!!!!

e na o je ena, tako da so ti členi 1, zdaj moraš pa samo še -1 vstaviti v enačbo in jo prsvilno izračunaš!!!!!

REšitev: 1 ali -1!!!?????

Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.

Zgodovina sprememb…

spremenilo: FrRoSt (17. okt 2020 ob 13:21)

Bikica195 :: 17. okt 2020, 13:45

Najlepša hvala vsem!
Torej se gleda e kot e⁰ . Torej če vstavim potem v odvod funkcije ta x= -1 in poračunam dobim k oz. smerni koeficient = 1

Bikica195 je 17. okt 2020 ob 13:45 izjavil:

Najlepša hvala vsem!
Torej se gleda e kot e⁰ . Torej če vstavim potem v odvod funkcije ta x= -1 in poračunam dobim k oz. smerni koeficient = 1

I walk. I look. I see. I stop. I photograph.

Zgodovina sprememb…

spremenilo: Bikica195 (17. okt 2020 ob 13:48)

bluefish :: 17. okt 2020, 13:50

Ne, e se ne gleda kot e^0. Po izračunu odvoda imaš za ta člen e^x+1. Ko v odvod vstaviš x = -1, dobiš e^0. Kolikšna je vrednost e^0 je pa stvar osnovnošolske matematike.

Zgodovina sprememb…

spremenil: bluefish (17. okt 2020 ob 13:52)

FrRoSt :: 17. okt 2020, 13:52

Bikica195 je 17. okt 2020 ob 13:45 izjavil:

Najlepša hvala vsem!
Torej se gleda e kot e⁰ . Torej če vstavim potem v odvod funkcije ta x= -1 in poračunam dobim k oz. smerni koeficient = 1

Bikica195 je 17. okt 2020 ob 13:45 izjavil:
Najlepša hvala vsem!
Torej se gleda e kot e⁰ . Torej če vstavim potem v odvod funkcije ta x= -1 in poračunam dobim k oz. smerni koeficient = 1

Tako!

dy/dx= 1 kar pomeni, da je v tej točki x=-1 sprememba y kar enaka spremembi x, kar pomeni, da je odvod premica pod kotom 45° oziroma pi/4!

Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.

smacker :: 17. okt 2020, 14:01

e je konstanta, podobno kot PI E (matemati%C4%8Dna konstanta) @ Wikipedia

Mali voz :: 18. okt 2020, 22:21

Kako bi pa za to funkcijo zapisal enačbo tangente? k in x torej že imaš, kako pa to n-ja?

FrRoSt :: 18. okt 2020, 23:09

Mali voz je 18. okt 2020 ob 22:21 izjavil:

Kako bi pa za to funkcijo zapisal enačbo tangente? k in x torej že imaš, kako pa to n-ja?

Odvod funkcije je ze zapis tangente na funkcijo!

Malo si poglej teme od @lara2, da ne boš spet septembra reševal letnik!! Ker smo ponovno v epodemiji... :))

Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.

_dragon_ :: 18. okt 2020, 23:48

FrRoSt je 18. okt 2020 ob 23:09 izjavil:

Odvod funkcije je ze zapis tangente na funkcijo!

Odvod funkcije seveda ni zapis tangente na funkcijo. Je samo naklon tangente: f'(x) = k
Za točko T(x,y), v kateri te zanima tangenta, rešiš enačbo y = f'(x)*x + n --> n = ...

Zgodovina sprememb…

spremenil: _dragon_ (18. okt 2020 ob 23:49)

FrRoSt :: 19. okt 2020, 19:53

_dragon_ je 18. okt 2020 ob 23:48 izjavil:

FrRoSt je 18. okt 2020 ob 23:09 izjavil:
Odvod funkcije je ze zapis tangente na funkcijo!

Odvod funkcije seveda ni zapis tangente na funkcijo. Je samo naklon tangente: f'(x) = k
Za točko T(x,y), v kateri te zanima tangenta, rešiš enačbo y = f'(x)*x + n --> n = ...

Tako!

Rabiš smerni koeficient in točko iz premice!

Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.

Mali voz :: 25. okt 2020, 17:48

Ali mi lahko kdo pove kako naj rešim nalogo:

Dana je funkcija f(x)= (x+2)e^x-1 , s Taylorjevim polinomom stopnje 2 ocenite vrednost f(x) v točki x=1,1

A110 :: 25. okt 2020, 18:01

https://brilliant.org/wiki/taylor-serie.... smao da racunas samo do drugega odvoda. tvoj x=1,1 toka a = 1, h=0,1

Mali voz :: 25. okt 2020, 19:50

Hvala, mi je bilo v pomoč.

Nikakor pa ne znam priti do prave rešitve odvoda funkcije ln(x²/(x+1)). Ali mi lahko kdo namigne pri katerem koraku zavijem v napačno smer?

Najprej odvajam kot naravni logaritem, dobim dvojni ulomek in ga obrnem, tako da mi pride prvi člen (x+1)/x²

Potem odvajam še tisto v oklepaju po pravilu ulomka in dobim: ((2x)(x+1)-(x²))/(x+1)² ..... x(x+2)/(x+1)(x+1)

nato vse skupaj združim: (x+1)/x² * x(x+2)/(x+1)(x+1)...... in še malo pokrajšam v (x+2)/x(x+1)....... ampak to menda ni pravilna rešitev.

Zgodovina sprememb…

spremenilo: Mali voz (25. okt 2020 ob 19:55)

Mali voz :: 25. okt 2020, 20:06

Izbira se med tremi rešitvami:

1. (x+1)/x²

2. 2((1/x) - (1/(x+1))

3. ( 2/x ) - (1/(x+1))

Zgodovina sprememb…

spremenilo: Mali voz (25. okt 2020 ob 20:07)

Mali voz :: 25. okt 2020, 23:40

Če koga zanima rešitev, pravilen je odgovor pod tretjo točko, ki pa je samo razširjena oblika mojega izzida, v tem je bil hakeljc, še ulomke bo treba izgleda ponovit.

Mali voz :: 1. nov 2020, 21:01

Ali lahko kdo na hitro pove kako se najbolj elegantno reši tole enačbo?

-e^x+1(x+2)=0

Unilseptij :: 1. nov 2020, 21:15

Mali voz je 1. nov 2020 ob 21:01 izjavil:

Ali lahko kdo na hitro pove kako se najbolj elegantno reši tole enačbo?

-e^x+1(x+2)=0

Ker je desna stran enaka nič, lahko ugotoviš, da imaš na levi strani produkt eksponentne (e^...) in linearne (x+2) funkcije. Tak produkt bo nič, če bo eden od faktorjev enak nič. Eksponentni del ni nikdar enak nič (razen v limiti, ko gre x proti minus neskončno), linarni del pa je nič, če je x=-2, kar je tudi končna rešitev.

Mali voz :: 1. nov 2020, 21:20

Super si razložu, hvala.

Bikica195 :: 10. nov 2020, 11:55

Spet novo vprašanje :))

Narisan imam graf neke funkcije (ni zapisana) in potrebno je še določiti kolikšen je NAKLON V TOČKI x=-4 -> k=___ IN x=0,5 -> k=___
Mi zna mogoče tudi brez, da bi videl graf povedati kako se izračuna te k - je? (fotografij še vedno ne znam priložiti sem -_-)

I walk. I look. I see. I stop. I photograph.

Zgodovina sprememb…

spremenilo: Bikica195 (10. nov 2020 ob 11:58)

Randomness :: 10. nov 2020, 12:02

V dani točki narišeš tangento (premico) na krivuljo in iz grafa odčitaš/izračunaš naklon te premice.

Bikica195 :: 10. nov 2020, 12:55

Bom še malo mogla premislit. Hvala :)

Kako se pa iz grafa odčita ali gre za sod/lih pol?

I walk. I look. I see. I stop. I photograph.

Mali voz :: 10. nov 2020, 13:49

A ima kdo kakšno idejo kako naj v WolframAlpha iskalnik napišem integral od 1 do -3 (?¹_-3), da mi ga bo pravilno zračunalo? Znak za integral imajo, ne vem pa kako številke zapisat, da bo ukaz deloval.

Zgodovina sprememb…

spremenilo: Mali voz (10. nov 2020 ob 13:50)

bluefish :: 10. nov 2020, 13:52

integrate [funkcija] between -3 and 1

ali

integrate [funkcija] from -3 to 1

Sicer pa: https://www.wolframalpha.com/examples/m...

Zgodovina sprememb…

spremenil: bluefish (10. nov 2020 ob 13:54)

Bikica195 :: 10. nov 2020, 18:54

Kako se napiše asimptotično obnašanje, če imaš napisano samo funkcijo: x² - 2X/ x² - x - 6

Pri tem pa nimaš narisanega grafa.

Rešitev je: lim, če gre x v minus neskončno je f(X) = 1 ; in če gre x v plus neskončno je lim f(x) =1

Hvala!

I walk. I look. I see. I stop. I photograph.

A110 :: 10. nov 2020, 19:11

tole je bolj srednješolska snov kot pa faks. pomisli kateri členi pri absolutno velikih vrednostih prevladajo

Mali voz :: 11. nov 2020, 16:29

Bikica195 je 10. nov 2020 ob 18:54 izjavil:

Kako se napiše asimptotično obnašanje, če imaš napisano samo funkcijo: x² - 2X/ x² - x - 6

Pri tem pa nimaš narisanega grafa.

Rešitev je: lim, če gre x v minus neskončno je f(X) = 1 ; in če gre x v plus neskončno je lim f(x) =1

Hvala!

Če sta stopnji polinoma v števcu in imenovalcu enaki, asimptoto izračunaš tako, da deliš koeficienta vodilnih členov, v tvojem primeru torej 1:1 = 1, asimptota je torej 1.

Asimptota deluje na funkcijo kot magnet, zato bo graf vedno težil k asimptoti, v tvojem primeru k 1, tako ko gre x v plus neskončno kot ko gre v minus neskončno, zato je takšen rezultat.

Mali voz :: 11. nov 2020, 16:41

Bikica195 je 10. nov 2020 ob 12:55 izjavil:

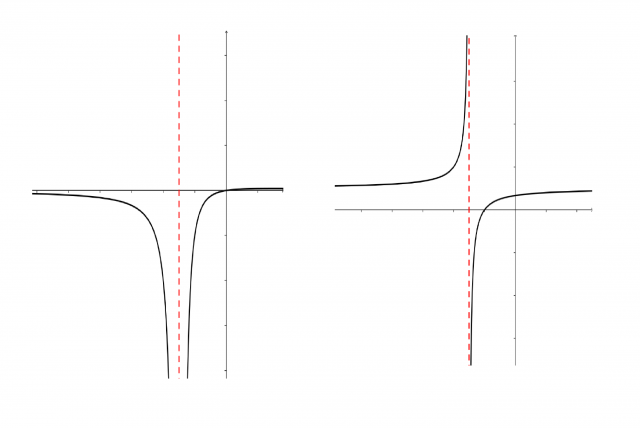
Kako se pa iz grafa odčita ali gre za sod/lih pol?

Tako, da opazuješ graf funkcije. Če je pol sodi, sta grafa na isti strani, če lihi, pa na nasprotni. Na sliki je desno primer lihega pola, levo pa sodega pola.

Zgodovina sprememb…

spremenilo: Mali voz (11. nov 2020 ob 16:44)

Bikica195 :: 11. nov 2020, 21:18

O najlepša hvala!

I walk. I look. I see. I stop. I photograph.

Mali voz :: 12. nov 2020, 23:31

Eno vprašanje na hitro. Kakšna je pravilna rešitev, če imaš v imenovalcu racionalne funkcije izraz x²(x² + 2)?

a.) Dobiš sodi pol v 0.
b.) Funkcija nima polov, ker se izraz v oklepaju ne da razcepiti
c.) Kaj tretjega

nergac :: 13. nov 2020, 05:33

Vse kar si napisal je pravilno.
Odvisno v kakem območju iščeš.

nergac :: 13. nov 2020, 05:58

Bo treba dodatno kavo spit.

Domena in kodomena sovpadata?

FrRoSt :: 13. nov 2020, 07:25

Mali voz je 12. nov 2020 ob 23:31 izjavil:

Eno vprašanje na hitro. Kakšna je pravilna rešitev, če imaš v imenovalcu racionalne funkcije izraz x²(x² + 2)?

a.) Dobiš sodi pol v 0.
b.) Funkcija nima polov, ker se izraz v oklepaju ne da razcepiti
c.) Kaj tretjega

A! funkcija ima v točki x=0 sodi pol
B! Izraz v oklepaju se da razcepit, je pa vedno večji od 0!
C! VELIKO tretjega!

Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.

nergac :: 13. nov 2020, 08:05

Točka B! posebej zanimiva je.

A je to nekaj v zvezi z veriženjem?

Kakorkoli, naj povedo drugi, tukaj nisem strokovnjak.

nergac :: 13. nov 2020, 08:11

Malce smo zašli, zato postavljam naslednje vprašanje:

Katera funkcija je racionalna:

(a) f: Q -> R
(b) f: C -> Q

Zgodovina sprememb…

spremenil: nergac (13. nov 2020 ob 08:11)

FrRoSt :: 13. nov 2020, 08:13

nergac je 13. nov 2020 ob 08:05 izjavil:

Točka B! posebej zanimiva je.

A je to nekaj v zvezi z veriženjem?

Kakorkoli, naj povedo drugi, tukaj nisem strokovnjak.

Točka B! velja samo za izraz v oklepaju in ne za celotno funkcijo!

To je malce dvoumno napisano in zavajajajoče! 8-)

Kaj pa če je v imenovalcu x na liho porenco!?? :))

To spada že v točko C!!

Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.

Bikica195 :: 29. nov 2020, 15:59

Rezultat mi je prišel 27 namesto -27. Ne vem jke sem se zmotila.

https://ncalculators.com/matrix/matrix-...
1. vrstica: -2 -2 1 1; 2. vrstica: -2 -2 -2 1; 3. vrstica: ,-2,-2,-2; 4.vrstica 1,1,-2,-2
REŠITEV= -27

I walk. I look. I see. I stop. I photograph.

Zgodovina sprememb…

spremenilo: Bikica195 (29. nov 2020 ob 16:02)

Balaton :: 29. nov 2020, 19:26

V 3. vrstici manjka števka. Fajn bi blo tudi videti postopek, nekje se ni upoštevalo predznaka.

Zgodovina sprememb…

spremenilo: Balaton (29. nov 2020 ob 19:28)

mirator :: 29. nov 2020, 23:15

V 3. vrstici res manjka številka v 4. stolpcu. Predvidevam, da je -2, vendar mi pride vrednost determinante 0.

Popravek. V tretji vrstici v prvem stolpcu mora biti številka 1, potem je vrednost determinante -27.

Zgodovina sprememb…

spremenil: mirator (29. nov 2020 ob 23:24)

2 3 »

Vredno ogleda ...

	Tema	Sporočila	Ogledi	Zadnje sporočilo
	Tema	Sporočila	Ogledi	Zadnje sporočilo
»	Odvod (strani: 1 2 ) Mali voz Oddelek: Šola	89	5287 (3565)	FrRoSt 30. avg 2020 10:09:54
»	matematika - pomoč mhwin Oddelek: Šola	21	3847 (2902)	lebdim 29. avg 2015 23:31:20
»	Matematika - pomoč (strani: 1 2 3 ) finpol1 Oddelek: Šola	104	26832 (23407)	daisy22 9. avg 2011 17:37:21
»	Matematika spl. matura 2011 (strani: 1 2 ) Mateja987 Oddelek: Šola	51	9516 (8138)	hexor 13. jul 2011 10:04:36
»	diferencialne enačbe Yosh Oddelek: Loža	11	3911 (3599)	overlord_tm 30. maj 2010 21:43:37

Več podobnih tem

Forum » Šola » Matematika - 1. letnik faksa

Matematika - 1. letnik faksa