Forum » Šola » Smiselnost integralov s drugim diferencialom
Smiselnost integralov s drugim diferencialom
marjan_h ::
Nisem ravno matematik, mogoče bo kakšen jype ali pa kdo drug s poglobljenim znanjem znal odgovoriti na:
Zakaj (to sem že večkrat opazil) pri zapisu integralov iz fizike dajo v integral neko količino ki ni odvisna od diferenciala. Recimo tukaj: primer
Pri izračunu masnega vztrajnostnega momenta dajo v integral r^2 pomnoženo s diferencialom dm. Ker seveda r^2 ni povezan s maso, daš konstanto pred integral, integriraš in dobiš m - 0, kar je r^2*m = J.
J = m*r^2, kar je enako kot originalna enačba na isti wiki strani.
Zakaj (to sem že večkrat opazil) pri zapisu integralov iz fizike dajo v integral neko količino ki ni odvisna od diferenciala. Recimo tukaj: primer
Pri izračunu masnega vztrajnostnega momenta dajo v integral r^2 pomnoženo s diferencialom dm. Ker seveda r^2 ni povezan s maso, daš konstanto pred integral, integriraš in dobiš m - 0, kar je r^2*m = J.
J = m*r^2, kar je enako kot originalna enačba na isti wiki strani.
jernejl ::
J = m*r^2
je vztrajnostni moment točkastega telesa.
Integral iz definicije pa je za splošno telo.
Lahko si ga predstavljaš kot vsoto vzrajnostnih momentov posameznih zelo majhnih koščkov telesa. Vsak košček telesa ima določeno maso in nek r. Radij r pa ni za vsako točko telesa enak, saj telo zavzema nek prostor.
je vztrajnostni moment točkastega telesa.
Integral iz definicije pa je za splošno telo.
Lahko si ga predstavljaš kot vsoto vzrajnostnih momentov posameznih zelo majhnih koščkov telesa. Vsak košček telesa ima določeno maso in nek r. Radij r pa ni za vsako točko telesa enak, saj telo zavzema nek prostor.
marjan_h ::
Ja vztrajnost točkastega telesa, ki se vrti po krožnici.
Matematično gledano pa s tem radijem na kvadrat s diferencialom dm ne moreš nič narediti. Razen če je r(m)^2.
Matematično gledano pa s tem radijem na kvadrat s diferencialom dm ne moreš nič narediti. Razen če je r(m)^2.
marjan_h ::
Aja, pa moja trditev je bila mišljena kot vprašanje:
Matematično gledano dati nekaj v integral, kar ni odvisno od diferenciala? Kakšna pripomba?
Drugo vprašanje je še:
Če imamo odvod npr. po času, dx/dt, kakšen določeni integral zapišemo (meje, od-do) da bomo dobili x? Mislim da je to eden od teoremov v infinitezimalnem računu, vendar se ne spomnim kateri.
Matematično gledano dati nekaj v integral, kar ni odvisno od diferenciala? Kakšna pripomba?
Drugo vprašanje je še:
Če imamo odvod npr. po času, dx/dt, kakšen določeni integral zapišemo (meje, od-do) da bomo dobili x? Mislim da je to eden od teoremov v infinitezimalnem računu, vendar se ne spomnim kateri.

Unknown_001 ::
Aja, pa moja trditev je bila mišljena kot vprašanje:
Matematično gledano dati nekaj v integral, kar ni odvisno od diferenciala? Kakšna pripomba?
Drugo vprašanje je še:
Če imamo odvod npr. po času, dx/dt, kakšen določeni integral zapišemo (meje, od-do) da bomo dobili x? Mislim da je to eden od teoremov v infinitezimalnem računu, vendar se ne spomnim kateri.
Meje nastaviš od t1 (čas začetnega dogodka) do t2 (čas končnega dogodka) nobene posebne znanosti ni. Integriranje je samo seštevanje diferencialno majhnih koščkov med dvema območjema - mejama. Pri nedoločenem integralu pa obvezno prišteješ konstanto, ki je navadno neznana oz pogojena z robnimi pogoji diferencialnega računa, na primer f(0)=0.
V integral daješ funkcijo kateri po domače zvišaš red oz. jo narediš odvisno od diferenciala. Ampak v tem primeru računaš nekaj drugega kot vrednost integrirane funkcije. Nekaj kar je soodvisno od funkcije ki jo integriraš, kot tudi od difernciala. Na primer računaš opravljeno delo po diferencialu poti.
A = Integrate(F*ds, {s1, s2})
F je lahko tudi spremenljiv, a zaenkrat naj bo konstanten.
ds od s1 do s2 je seštevek poti od položaja s1 do položaja s2. Pomnoženo z neodvisno konstanto F to pomeni delo opravljeno na tej poti.
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
marjan_h ::
Torej če pravilno razumem, za tvoj primer delo je F(s)*ds bolj eksplicitno povedano (če bi bil spremenljiv)?
Če pa ni spremenljiv pa ga lahko dodamo pred integral?
In ko računamo F(s)*ds s tem povemo da je recimo pri 1m poti sila 5N, pri 2m pa 10 N in tako naprej seveda kot primer?
Če pa ni spremenljiv pa ga lahko dodamo pred integral?
In ko računamo F(s)*ds s tem povemo da je recimo pri 1m poti sila 5N, pri 2m pa 10 N in tako naprej seveda kot primer?

Unknown_001 ::
Ne, sila je konstantna. Outcome zmnožka (delo) je drugačen.
S skupni = integrirano ds od s1 do s2
S skupni = integrirano ds od s1 do s2
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
moose_man ::
Ko rešuješ integral za vztrajnostni moment, običajno integral po masi prevedeš na integral po prostornini:
dm = rho * dV ,
kjer rho označuje gostoto telesa. Če zavoljo razlage predpostavimo, da je gostota po celem telesu konstantna in če delamo v kartezičnih koordinatah, potem dobiš takle izraz za vztrajnostni moment. Ker Latex očitno ne dela, sem na nekem online editorju na hitro naredil slikico, upam da pomaga:
Morda je zdaj lazje vidno, kako/zakaj je pozicijski vektor odvisen od mase. Ampak se bolje je, ce gres na internet (morda zna bit ze wiki dovolj) poiskat razlago vztrajnostnega momenta, da bos razumel.
dm = rho * dV ,
kjer rho označuje gostoto telesa. Če zavoljo razlage predpostavimo, da je gostota po celem telesu konstantna in če delamo v kartezičnih koordinatah, potem dobiš takle izraz za vztrajnostni moment. Ker Latex očitno ne dela, sem na nekem online editorju na hitro naredil slikico, upam da pomaga:
Morda je zdaj lazje vidno, kako/zakaj je pozicijski vektor odvisen od mase. Ampak se bolje je, ce gres na internet (morda zna bit ze wiki dovolj) poiskat razlago vztrajnostnega momenta, da bos razumel.
Zgodovina sprememb…
- spremenilo: moose_man ()

Unknown_001 ::
Brezveze da mu vztrajnostne momente razlagamo.
Koncept integriranja mora razumet.
directx11
Ti poznaš fizikalne formule ala F = p*A. To je zelo posplošena formula, kjer imaš znane veličine. Če pa ploščina ni znana, moraš včasih le to izračunati s pomočjo ploskovnega integrala. Zato imaš dF(normale) = p*dA. V tem primeru lahko s to splošno enačbo ob poznavanju mej ploskve poračunaš kakšen je tlak na ploskev znotraj teh mej.
Koncept integriranja mora razumet.
directx11
Ti poznaš fizikalne formule ala F = p*A. To je zelo posplošena formula, kjer imaš znane veličine. Če pa ploščina ni znana, moraš včasih le to izračunati s pomočjo ploskovnega integrala. Zato imaš dF(normale) = p*dA. V tem primeru lahko s to splošno enačbo ob poznavanju mej ploskve poračunaš kakšen je tlak na ploskev znotraj teh mej.
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
marjan_h ::
Si bom pogledal video, vztrajnostni moment sem dal samo kot primer. Sicer je teh primerov iz fizike z integrali veliko, zato mislim da je pametno razumeti osnove.
Nadaljnja vprašanja sledijo...
Nadaljnja vprašanja sledijo...

Unknown_001 ::
Si bom pogledal video, vztrajnostni moment sem dal samo kot primer. Sicer je teh primerov iz fizike z integrali veliko, zato mislim da je pametno razumeti osnove.
Nadaljnja vprašanja sledijo...
Ti bom poskusil razložit za vztrajsnotni moment:
Če imaš
J=r^2*m za točkasto telo (poenostavljeno da ni treba vztrajnostnih momentov telesa računat) ne rabiš integriranja.
Če pa upoštevaš vse masne točke (neskončno) pa si moraš pomagati z integralom, sa katerim popišeš prav vse. Seveda je neskončno točk a tudi ti lahko z integralom izračunaš neskončno majhne koščke in "in theory" popišeš vse v nekih mejah.
Za sistem z neskončno M točkami, pa moraš uporabiti diferencialni račun da lahko popišeš vse.
Na primer za valj. Veš da je J ene diferencialno majhne točke okoli težiščne osi enak r^2*dm
Za pas točk na konstantnem radiju velja v cilindričnih koordinatah:
J = r^2 * M ker so vse točke na enaki oddaljenosti. Realno tako telo nima mase ampak vseeno zgolj teoretični primer. Maso znamo izračunati s pomočjo volumna in gostote. V tem primeru je nerelevantno ubrati tak pristop. Lahko imaš podano ali pa imaš radij ali višino zanemarjena. ter dm računaš kot ro (po kotu) * dphi. Ampak bolje bom v nadaljevanju razložil.
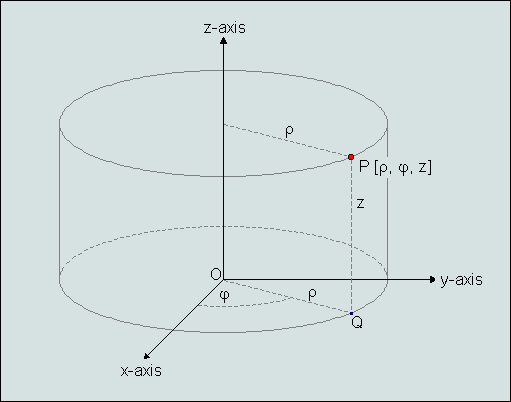
Za polno telo- valj, kjer imaš razpon radija od 0-R pa ta radij postane pomemben v diferencialni enačbi. kako? Pozor, delamo v cilindričnem koordinatnem sistemu, zato velja da x = r*cos(fi), y = r*sin(fi), z=z . Ob pretvorbi dobimo produkt Jakobijeve matrike r, ki ga moramo primnožiti, da se nam transformacija na druge koordinate izide.
torej imamo J= Integrate( r^2*dm *r, {m1, m2})
Tu si ne moremo kaj dosti pomagati, ker ne vemo mej za diferencial mase, zato moramo stvar preurediti. Vemo, da maso telesa lahko zapišemo kot zmnožek gostote in volumna.
dm = ro*dV ali po domače masa pri konstantni gostoti rase z volumnom.
dV = dx*dy*dz ali analogno na kvader V = x*y*z dimenzije le da pri integralu delaš med mejami od x1 do x2, od y1 do y2, od z1 do z3 kjerkoli v KS. x = širina, y = dolžina, z = višina
Za cilindrični sistem
dV = dr * dphi* dz
dm = ro * dr * dphi* dz (to pa so pametne stvari za katere poznamo meje)
ro - gostota je konstantna.
dr - radij cilindra vemo da je od 0 do R
dfi - kot zasuka vemo da je polni obrat v radianih 2pi
dz - dolžina valja od z1 do z2
Pomagaj si s slikico. Recimo to je podobno kot bi rezal kos torte (valj) po navodilih. za naš primer celo torto :D
Za ta kos torte meje
dr od 0 do R (od sredine do roba torte na razdalji R)
dz od krožnika do vrha torte
dfi kot od enestrani reza do druge strani reza :D
Analogno ti poskušam pokazati katero območje točk smo popisali z integriranjem. Upam da nisi lačen ;P
Vrnimo se na integral.
J = Integrate(r^3*ro , {r1=0,r2=R}, {phi 1=0, phi 2 = 2pi (polni obrat), z1 = neki, z2 = neki več})
Torej tu lahko izvedemo integralski račun. r^3 imamo zato ker smo morali zaradi pretvorbe KS upoštevati r !
Jacobijeva matrika @ Wikipedia
Torej izvedemo klasično integracijo.
Najprej po r in dobimo ro* r^4 / 4 *dphi *dz.
Nato integriramo po phi in dobimo 2 pi * ro * r^4 / 4 *dz in še po z da dobimo 2 pi * ro * r^4 / 4 * z.
Vemo, da je pi*r^2 = ploščina. Vemo, da je ploščina krat višina z (med z1 in z2) enaka Volumnu.
In vemo ,da je Volumen krat gostota enako masa valja.
Dobimo (ro*z*2pi*r^2) * (2*r^2 / 4) = (M * r^2) / 2
Zgodovina sprememb…
- spremenilo: Unknown_001 ()

Unknown_001 ::
Pardon pri integriranju po ko maš dm od navideznih mej m1 do m1 ignoriraj primnožek r, ker sem hotel nekaj v cilindričnih zmutit.
Tam itak ni relevantno ker ne moreš postavit meje od mase nekaj1 do mase nekaj2. Ni koordinatnega sistema da bi lahko obravnaval po meje po masi. Lahko si ga izmisliš ampak good luck pri praktični rabi ki je ni.
Tam itak ni relevantno ker ne moreš postavit meje od mase nekaj1 do mase nekaj2. Ni koordinatnega sistema da bi lahko obravnaval po meje po masi. Lahko si ga izmisliš ampak good luck pri praktični rabi ki je ni.
Zgodovina sprememb…
- spremenilo: Unknown_001 ()

Unknown_001 ::
A110 ::
mizori oblak je kuharski prirocnik  so pa tole res osnove ki bi jih moral razumeti tudi tisti ki mu matematika ne gre najbolje
so pa tole res osnove ki bi jih moral razumeti tudi tisti ki mu matematika ne gre najbolje

Unknown_001 ::
mizori oblak je kuharski prirocnikso pa tole res osnove ki bi jih moral razumeti tudi tisti ki mu matematika ne gre najbolje
Pa mi smo inđeniri
Na kratko. Ja pri nas je poudarek na rabi (logično) pri vas na razumevanju. Je pa res, da bi vsak inženir ki je nekaj vreden, moral tudi tist vaš teoretični del dobro razumet.
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
joze67 ::
Aja, pa moja trditev je bila mišljena kot vprašanje:
Matematično gledano dati nekaj v integral, kar ni odvisno od diferenciala? Kakšna pripomba?
Če je stvar konstanta jo pač lahko izpostaviš. Včasih tudi ne, če sama oblika integrirane funkcije spominja na kaj, kar pomaga v nadaljevanju.
Tvoj konkreten primer pa ni tak - napačen primer za vprašanje. Integriraš po trorazsežnem prostoru, radij seveda je še kako odvisen od tega, kje v tem prostoru ta hip operiraš, dm pa je v resnici gostota (\rho) * dV. In gostota v splošnem tudi ni enaka podvsod.
St753 ::
Se mi zdi, da ti v odgovorih zgoraj niso cist jasno odgovorili (razen joze), tako da ti bom se jst probal razlozit. Ce je x neodvisen od obmocja integriranja, pomeni da bo med 'sestevanjem' kosckov, kot so omenili zgoraj, konstanten in ga lahko izpostavis. Kot je ze joze povedal, se v tvojem primeru r spreminja med integriranjem, zato ga ne mores postavit pred integral.
Za vprasanje kako integrirati dx/dt, da dobis x: integriral bi med 0 in x. Ker vrednost integrala ni uniquely determined, ce imas podan odvod (temu primerno potem ime nedolocen integral za inverzno operacijo), moras za izbrano zacetno vrednost primerno nastavit spodnjo mejo. Ce je ta enaka nic, potem samo integriras od 0.
Ce kaj ne drzi, me popravite ostali.
Za vprasanje kako integrirati dx/dt, da dobis x: integriral bi med 0 in x. Ker vrednost integrala ni uniquely determined, ce imas podan odvod (temu primerno potem ime nedolocen integral za inverzno operacijo), moras za izbrano zacetno vrednost primerno nastavit spodnjo mejo. Ce je ta enaka nic, potem samo integriras od 0.
Ce kaj ne drzi, me popravite ostali.
marjan_h ::
Hvala vsem, sedaj razumem zakaj ne morem r^2 dati pred integral. Najbolj specifično na to je odgovoril @justdoit.
Ali se potem takšen integral edino reši tako kot sta pokazala @Raptor F16 in @moose_man?
Torej prevedem integral na trojni integral. Ali ne obstaja noben matematični postopek za direktni napad na takšne vrste integral, torej moram vedeti da je masa enaka gostoti krat volumnu ipd...?
Kako bi matematik rešil takšen integral, brez da bi vedel o fiziki?
Ali se potem takšen integral edino reši tako kot sta pokazala @Raptor F16 in @moose_man?
Torej prevedem integral na trojni integral. Ali ne obstaja noben matematični postopek za direktni napad na takšne vrste integral, torej moram vedeti da je masa enaka gostoti krat volumnu ipd...?
Kako bi matematik rešil takšen integral, brez da bi vedel o fiziki?

Unknown_001 ::
Hvala vsem, sedaj razumem zakaj ne morem r^2 dati pred integral. Najbolj specifično na to je odgovoril @justdoit.
Ali se potem takšen integral edino reši tako kot sta pokazala @Raptor F16 in @moose_man?
Torej prevedem integral na trojni integral. Ali ne obstaja noben matematični postopek za direktni napad na takšne vrste integral, torej moram vedeti da je masa enaka gostoti krat volumnu ipd...?
Kako bi matematik rešil takšen integral, brez da bi vedel o fiziki?
Odvisno kako imaš definiran dm. Lahko bi definiral tudi s spremenljivo gostoto. Lahko ga definiraš po dolžini na primer da imaš gostoto podatno kot kilograme na meter in nato integriraš po razdalji namesto po prostoru. Odvisno koliko dimenzij bi rad zanemaril, da si poenostaviš računanje. Odvisno od primera. Najbolj splošno je za take primere delati v treh dimenzijh.
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
marjan_h ::
Unknown_001 je izjavil:
Hvala vsem, sedaj razumem zakaj ne morem r^2 dati pred integral. Najbolj specifično na to je odgovoril @justdoit.
Ali se potem takšen integral edino reši tako kot sta pokazala @Raptor F16 in @moose_man?
Torej prevedem integral na trojni integral. Ali ne obstaja noben matematični postopek za direktni napad na takšne vrste integral, torej moram vedeti da je masa enaka gostoti krat volumnu ipd...?
Kako bi matematik rešil takšen integral, brez da bi vedel o fiziki?
Odvisno kako imaš definiran dm. Lahko bi definiral tudi s spremenljivo gostoto. Lahko ga definiraš po dolžini na primer da imaš gostoto podatno kot kilograme na meter in nato integriraš po razdalji namesto po prostoru. Odvisno koliko dimenzij bi rad zanemaril, da si poenostaviš računanje. Odvisno od primera. Najbolj splošno je za take primere delati v treh dimenzijh.
Ja, vendar matematik o tem nič ne ve. Jaz predpostavljam, da imamo samo integral, vemo da je r^2 odvisen (torej mora ostati znotraj integrala).
Ali je sploh rešljiv na takšen način? (Pozor, matematično!)

Unknown_001 ::
Unknown_001 je izjavil:
Hvala vsem, sedaj razumem zakaj ne morem r^2 dati pred integral. Najbolj specifično na to je odgovoril @justdoit.
Ali se potem takšen integral edino reši tako kot sta pokazala @Raptor F16 in @moose_man?
Torej prevedem integral na trojni integral. Ali ne obstaja noben matematični postopek za direktni napad na takšne vrste integral, torej moram vedeti da je masa enaka gostoti krat volumnu ipd...?
Kako bi matematik rešil takšen integral, brez da bi vedel o fiziki?
Odvisno kako imaš definiran dm. Lahko bi definiral tudi s spremenljivo gostoto. Lahko ga definiraš po dolžini na primer da imaš gostoto podatno kot kilograme na meter in nato integriraš po razdalji namesto po prostoru. Odvisno koliko dimenzij bi rad zanemaril, da si poenostaviš računanje. Odvisno od primera. Najbolj splošno je za take primere delati v treh dimenzijh.
Ja, vendar matematik o tem nič ne ve. Jaz predpostavljam, da imamo samo integral, vemo da je r^2 odvisen (torej mora ostati znotraj integrala).
Ali je sploh rešljiv na takšen način? (Pozor, matematično!)
Glej, če dm v tej enačbi po definiciji fizikalnega modela ne zahteva integriranja direktno ali posredno po r, potem r v vsakem primeru izvisi kot konstanta. Torej, če r kot dimenzija ne vpliva na maso. Če z njim definiraš področje širše področje (ki ni konstantno), v katerem je ta masa prerazporejena potem ga MORAŠ upoštevati.
Ti v fizikalnem modelu določiš katere prostostne stopnje boš zanemaril. Na primer, če imaš neko cev velikega notranjega radija s tanko steno, ki se vrti okoli težiščne osi, lahko stvar poenostaviš, da so vse točke na istem radiju (zanemariš debelino). To je poenostavitev. In v tem primeru r obravnavaš kot konstanto. Vztrajnostni moment bo enak kot da bi imel točkasto maso na tem radiju, le da je v primeru lupine razporejena po plašču. In z dm ti izračunaš maso, ki je porazdeljena. Lahko pa je direkt podana. Potem lahko sistem še bolj sklestiš, če imaš maso znano. Res pa je, da pri deviacijskih momentih tega ne smeš storiti, da poenostaviš v eno samo točko ampak to je druga snov.
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
mirator ::
DirectX11 si je očitno ta forum vzel za osebno izobraževanje, kar sicer ni nič narobe. Narobe pa je, da dobi kopico informacij, ki pa si medsebojno tudi nasprotujejo in tako pridobljeno znanje je v praksi lahko relativno nevarno.
Tokratno vprašanje žal zahteva odgovor z znajem fizike in matematike.
Navedeni integral velja za vztrajnostni moment telesa, ki rotira okoli svoje osi. Ker gre za telo, pomeni da gre za tridimenzionalni prostor oz. 3D koordinatni sistem. Pri tem r pomeni vektor, ki je podan s koordinatami x, y, in z ter maso telesa, ki je odvisna od specifične teže (ro) in diferenciala volumna dV. Pri tem je r^2 = x^2 + y^2 + z^2 in diferencial volumna dV = dx*dy*dz. Iz tega torej sledi, da r ni nobena konstanta. V tem integralu je konstanta samo specifična teža (ro).
Tokratno vprašanje žal zahteva odgovor z znajem fizike in matematike.
Navedeni integral velja za vztrajnostni moment telesa, ki rotira okoli svoje osi. Ker gre za telo, pomeni da gre za tridimenzionalni prostor oz. 3D koordinatni sistem. Pri tem r pomeni vektor, ki je podan s koordinatami x, y, in z ter maso telesa, ki je odvisna od specifične teže (ro) in diferenciala volumna dV. Pri tem je r^2 = x^2 + y^2 + z^2 in diferencial volumna dV = dx*dy*dz. Iz tega torej sledi, da r ni nobena konstanta. V tem integralu je konstanta samo specifična teža (ro).

noraguta ::
praviloma tegale ne boš delal v kartezičnem. ampak vrtenino rešuješ v kompleksnem.
Pust' ot pobyedy k pobyedye vyedyot!

Unknown_001 ::
DirectX11 si je očitno ta forum vzel za osebno izobraževanje, kar sicer ni nič narobe. Narobe pa je, da dobi kopico informacij, ki pa si medsebojno tudi nasprotujejo in tako pridobljeno znanje je v praksi lahko relativno nevarno.
Tokratno vprašanje žal zahteva odgovor z znajem fizike in matematike.
Navedeni integral velja za vztrajnostni moment telesa, ki rotira okoli svoje osi. Ker gre za telo, pomeni da gre za tridimenzionalni prostor oz. 3D koordinatni sistem. Pri tem r pomeni vektor, ki je podan s koordinatami x, y, in z ter maso telesa, ki je odvisna od specifične teže (ro) in diferenciala volumna dV. Pri tem je r^2 = x^2 + y^2 + z^2 in diferencial volumna dV = dx*dy*dz. Iz tega torej sledi, da r ni nobena konstanta. V tem integralu je konstanta samo specifična teža (ro).
To kaj lahkobpoenostaviš in česa ne smeš jebodvisno od fizikalnega modela.
Sicer pa... vse skupaj je brezveze. To je tako kot imet na inštrukcijah nekoga, ki si niti osnov ni prebral. Te zadeve presegajo njegov domet in dokler ne bo razčistil snovi za nazaj mu ne bo jasno kaj smo mu hoteli povedati. Druge ni, kot da se loti predelat poglavje Analize od začetka, nato pa še osnove fizike.
Vse ostalo bo neko tolmačenje od katerega ne bo odnesel ničesar.
@OP najprej si razčisti osnove. Nauči se limite, vektorje, odvajanje in integriranje, sploh pa parcialnobodvajanje in mnogotere integrale.
Potem pa glej razlage v fiziki, ko boš dovolj matematično podkovan. Šele nato ti bodo tisti zapisi z integrali jasni.

noraguta ::
Modeliranje problema je precej zahtevna disciplina, ki zahteva tako širino kot odlično poznovanje matematičnih orodij. V osnovi so nas vse naučili principe, ko prideš do detajlov pa ni več tak hec. Dostikrat se zadovoljimo že z modeli kateri vsaj približno opišejo sistem.
Pust' ot pobyedy k pobyedye vyedyot!
mirator ::
Unknown_001 je izjavil:
To kaj lahkobpoenostaviš in česa ne smeš jebodvisno od fizikalnega modela.
Sicer pa... vse skupaj je brezveze. To je tako kot imet na inštrukcijah nekoga, ki si niti osnov ni prebral. Te zadeve presegajo njegov domet in dokler ne bo razčistil snovi za nazaj mu ne bo jasno kaj smo mu hoteli povedati. Druge ni, kot da se loti predelat poglavje Analize od začetka, nato pa še osnove fizike.
Vse ostalo bo neko tolmačenje od katerega ne bo odnesel ničesar.
@OP najprej si razčisti osnove. Nauči se limite, vektorje, odvajanje in integriranje, sploh pa parcialnobodvajanje in mnogotere integrale.
Potem pa glej razlage v fiziki, ko boš dovolj matematično podkovan. Šele nato ti bodo tisti zapisi z integrali jasni.
Se popolnoma strinjam s tabo.
marjan_h ::
Sedaj je tema prešla na poduk.
V bistvu ni bilo nič brezveze, ker sedaj vem zakaj ne smem r^2 izpostaviti. Jaz poznam matematična orodja, samo včasih se mi zatakne ker imeti žive predstave o tem kaj računaš je zelo težko. Zato se vsi zadovoljimo da rečemo da je npr. odvod od x^2 enak 2x in več ne razmišljamo o tem iz kje izhaja.
Sicer pa koga pa naj vprašam kot programerja/matematika/fizika/strojnika, ki o tem dnevno razmišlja. Pa hvala Raptor F16 za tale kanal na youtube, sploh nisem vedel da obstaja.
Sem imel še eno vprašanje, vendar se sedaj ne spomnim...
V bistvu ni bilo nič brezveze, ker sedaj vem zakaj ne smem r^2 izpostaviti. Jaz poznam matematična orodja, samo včasih se mi zatakne ker imeti žive predstave o tem kaj računaš je zelo težko. Zato se vsi zadovoljimo da rečemo da je npr. odvod od x^2 enak 2x in več ne razmišljamo o tem iz kje izhaja.
Sicer pa koga pa naj vprašam kot programerja/matematika/fizika/strojnika, ki o tem dnevno razmišlja. Pa hvala Raptor F16 za tale kanal na youtube, sploh nisem vedel da obstaja.
Sem imel še eno vprašanje, vendar se sedaj ne spomnim...

noraguta ::
Sedaj je tema prešla na poduk.
V bistvu ni bilo nič brezveze, ker sedaj vem zakaj ne smem r^2 izpostaviti. Jaz poznam matematična orodja, samo včasih se mi zatakne ker imeti žive predstave o tem kaj računaš je zelo težko. Zato se vsi zadovoljimo da rečemo da je npr. odvod od x^2 enak 2x in več ne razmišljamo o tem iz kje izhaja.
Sicer pa koga pa naj vprašam kot programerja/matematika/fizika/strojnika, ki o tem dnevno razmišlja. Pa hvala Raptor F16 za tale kanal na youtube, sploh nisem vedel da obstaja.
Sem imel še eno vprašanje, vendar se sedaj ne spomnim...
Kuši oljer. Ne vem kako poznaš orodja jih pa ne razumeš.
Se pa v praksi pri inženiringu probajo stvari če se le da na linearne probleme. Že zaradi "debugiranja" .
Pust' ot pobyedy k pobyedye vyedyot!
Zgodovina sprememb…
- spremenilo: noraguta ()
marjan_h ::
Kaj to pomeni "Kuši oljer"?
Jaz sem se naučil integrirati in odvajati tako kot večina gimnazijcev. Samo da opraviš test in potem pozabiš. Sedaj imam pa probleme s razumevanjem, in tukaj sprašujem .
.
Jaz sem se naučil integrirati in odvajati tako kot večina gimnazijcev. Samo da opraviš test in potem pozabiš. Sedaj imam pa probleme s razumevanjem, in tukaj sprašujem

noraguta ::
Gre za to kaj se da in kaj se splača odvajat. Kuši ojler stvar sparvlja na najmanjši skupni imenovalc ki je ponavadi še uporaben.
https://en.m.wikipedia.org/wiki/Cauchy-...
Ne skrb če si pozabil jaz sem za bernika znal pol bronštajna na pamet. Pa sem potem se za konkretne zadeve na novo učil. Je pa res da gre potem hitreje.
https://en.m.wikipedia.org/wiki/Cauchy-...
Ne skrb če si pozabil jaz sem za bernika znal pol bronštajna na pamet. Pa sem potem se za konkretne zadeve na novo učil. Je pa res da gre potem hitreje.
Pust' ot pobyedy k pobyedye vyedyot!
marjan_h ::
Dajte še kakšen primer, kjer je potrebno imeti znanje fizike da rešiš matematični integral. 

noraguta ::
Dajte še kakšen primer, kjer je potrebno imeti znanje fizike da rešiš matematični integral.
Že s=vt lahko postaviš na različne načine na koordinatni sistem. Če gre za nelinearni pospešek maš pa že cel integral namest pravokotnega trikotnika. Čeprov na konc spet delaš sumo teh trikotnikov(trapezov) .
Pust' ot pobyedy k pobyedye vyedyot!

noraguta ::
Sicer ma pa oldi enk super temo sedaj na forumu kjer kalibrira tust svoj uklonski spektrometer. Ni problem sama matematka ampak kaj nucaš izvedet.
Pust' ot pobyedy k pobyedye vyedyot!
D3m0r4l1z3d ::
Prepozno sem opazil temo, so že drugi vse povedali. Lahko filozofiram, če želite.
Te rabimo pri špekulacijah, tukaj brez veze.
ETN Wallet addr.: etnkGuvhDzR7Dh8us4e69VStubGbmQHrh5pe2fnpNDhEhX5
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus

jype ::
D3m0r4l1z3d je izjavil:
Te rabimo pri špekulacijah, tukaj brez veze.Piše se "z drugim diferencialom".
D3m0r4l1z3d ::
Model je gimnazijo naredil pa ne pozna *ta suhi škafec pušča*.
ETN Wallet addr.: etnkGuvhDzR7Dh8us4e69VStubGbmQHrh5pe2fnpNDhEhX5
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
Zgodovina sprememb…
- spremenilo: D3m0r4l1z3d ()

Unknown_001 ::
D3m0r4l1z3d je izjavil:
Model je gimnazijo naredil pa ne pozna *ta suhi škafec pušča*.
Vseen ni tko hudo ko eni, ki naredijo faks pa da na konc delajo kot nek komercialist.
D3m0r4l1z3d ::
Prodajni inženir. Malo bolje kot prodajalka sem, tako da sem zadovoljen 
S spoštovanjem do fizikov in/ali matematikov!
S spoštovanjem do fizikov in/ali matematikov!
ETN Wallet addr.: etnkGuvhDzR7Dh8us4e69VStubGbmQHrh5pe2fnpNDhEhX5
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
Zgodovina sprememb…
- spremenilo: D3m0r4l1z3d ()

Unknown_001 ::
D3m0r4l1z3d je izjavil:
Prodajni inženir. Malo bolje kot prodajalka sem, tako da sem zadovoljen
What? Dejansko? To si po fohu?
Kristusove gate. Pa kaj zdaj vsakemu kekcu dajo naziv inženir? Zame si prodajnik in konc. Ista bruleska kot inženir vodarstva in okolja a v bistvu je komunalc.
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
D3m0r4l1z3d ::
Upam, da ločiš med poklicem in delavnim mestom. To, da si agresivno pasiven pa vem že od ene prejšnje teme.
ETN Wallet addr.: etnkGuvhDzR7Dh8us4e69VStubGbmQHrh5pe2fnpNDhEhX5
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
Zgodovina sprememb…
- spremenilo: D3m0r4l1z3d ()

Unknown_001 ::
D3m0r4l1z3d je izjavil:
Upam, da ločiš med poklicom in delavnim mestom. To, da si agresivno pasiven pa vem že od ene prejšnje teme.
1. Pasivno 2. Agresiven
Btw. Ti si se nekaj na OP a spravljal. Kako možeš, da mi se žališ.
D3m0r4l1z3d ::
Današnjo mladino lahko naučiš matematike, sppštovanja do drugih pa ne, đizs!
ETN Wallet addr.: etnkGuvhDzR7Dh8us4e69VStubGbmQHrh5pe2fnpNDhEhX5
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
D3m0r4l1z3d ::
Ja, očitno je ne pozna pa se dela pametnega. Toliko je pasiven, da je že kar agresiven 
ETN Wallet addr.: etnkGuvhDzR7Dh8us4e69VStubGbmQHrh5pe2fnpNDhEhX5
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus

Unknown_001 ::
D3m0r4l1z3d je izjavil:
Današnjo mladino lahko naučiš matematike, sppštovanja do drugih pa ne, đizs!
Spoštovanje ni samoumevno. Če boš tibpizda do drugih bom tudi jaz pizda do tebe.
Srečnga pa zdravga. Jst grem nazaj biftek mlatit.
D3m0r4l1z3d ::
No, zdaj si se pa izdal. Pazi, surovo meso te naredi celo pasivno agresivnega.
ETN Wallet addr.: etnkGuvhDzR7Dh8us4e69VStubGbmQHrh5pe2fnpNDhEhX5
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
A1nCWrFBMK2NmkycgVN4sAwhvY8YyNNbF6KUSJyFZ99QKU8phCn
Cryptopia ref. link: https://www.cryptopia.co.nz/Register?referrer=Anymalus
Zgodovina sprememb…
- spremenilo: D3m0r4l1z3d ()
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Fizika osnovna nalogaOddelek: Šola | 2764 (1938) | robcek23 |
| » | Fizika - avtomobilOddelek: Šola | 3838 (2192) | marjan_h |
| » | pi na maturi (strani: 1 2 )Oddelek: Šola | 11362 (9482) | Smurf |
| » | Trije integrali pomoč!!!Oddelek: Šola | 4374 (3840) | Math Freak |
| » | težišče valjaOddelek: Šola | 1888 (1665) | MeGreat |