Forum » Šola » Zmeda z definicijo koordinatnih sistemov
Zmeda z definicijo koordinatnih sistemov

Unknown_001 ::
Rešujem matematični problem za katerega moram uporabiti sferični koordinatni sistem in opažam, da obstajata dva načina popisa.
Razlikujeta se le v definiciji kota med ploskvijo XY in Z osjo.
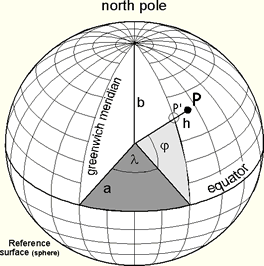
Primer kot je opisam v slovenskih učbenikih in skriptah.
Torej po tej definiciji za:
x = cosΦcosΛ
y = cosΦsinΛ
z = sinΦ
Primer iz drugih skript
x = sinΘcosΦ
y = sinΘsinΦ
z = cosΘ
Torej v čem je problem. Delam na nekem primeru in ugotavljam, da je uporaba drugega zapisa velikokrat lažja. Točno ta, druga varianta uporabljena v vseh tujih učbenikih kjer se obravnava matematika. Prva pa je kakor sedaj malo raziskujem kvečjem bolj uporabljana v geografiji za popis koordinat na zemlji.
Zdaj me pa zanima, zakaj ni nekega standardnega dogovora glede tega ali pa vsaj pojasnila kje je kateri bolj uporabljan. Ok, razumem, da je teoretično oboje isti "šmorn" za uporabo. Je pa moteče, da vsak profesor pove svojo definicijo. Eni razlagajo prvo ostali drugo varianto, nihče pa konkretno ne pove zakaj se uporabljata dve različni definiciji, če je res vseeno po kateri delaš. Potem bi lahko kot ki leži na XY ploskvi definiral tudi v smeri od Y proti X če gremo mal komplicirat, pa bi se enako dalo prit do rezultata a tega nihče ne uporablja (verjetno iz praktičnih razlogov).
Glavno vprašanje. Ali ima katera od zapisanih variant kje kakšno praktično posebno prednost? Je tu kak poznavalec, ker me res zanima ali obstaja praktična razlika.
Razlikujeta se le v definiciji kota med ploskvijo XY in Z osjo.
Primer kot je opisam v slovenskih učbenikih in skriptah.
Torej po tej definiciji za:
x = cosΦcosΛ
y = cosΦsinΛ
z = sinΦ
Primer iz drugih skript
x = sinΘcosΦ
y = sinΘsinΦ
z = cosΘ
Torej v čem je problem. Delam na nekem primeru in ugotavljam, da je uporaba drugega zapisa velikokrat lažja. Točno ta, druga varianta uporabljena v vseh tujih učbenikih kjer se obravnava matematika. Prva pa je kakor sedaj malo raziskujem kvečjem bolj uporabljana v geografiji za popis koordinat na zemlji.
Zdaj me pa zanima, zakaj ni nekega standardnega dogovora glede tega ali pa vsaj pojasnila kje je kateri bolj uporabljan. Ok, razumem, da je teoretično oboje isti "šmorn" za uporabo. Je pa moteče, da vsak profesor pove svojo definicijo. Eni razlagajo prvo ostali drugo varianto, nihče pa konkretno ne pove zakaj se uporabljata dve različni definiciji, če je res vseeno po kateri delaš. Potem bi lahko kot ki leži na XY ploskvi definiral tudi v smeri od Y proti X če gremo mal komplicirat, pa bi se enako dalo prit do rezultata a tega nihče ne uporablja (verjetno iz praktičnih razlogov).
Glavno vprašanje. Ali ima katera od zapisanih variant kje kakšno praktično posebno prednost? Je tu kak poznavalec, ker me res zanima ali obstaja praktična razlika.
Wie nennt man einen Moderator mit der Hälfte des Gehirnis ?
Begabt
Begabt
onitam ::
Jaz poznam le drugega, kot je v angleški in nemški literaturi. Verjetno smo slovenci podedovali prvega iz časov skupne države, le da bi bili drugačni od drugih. Kot še marsikje drugje.
bleh

jype ::
Jaz poznam le drugega, kot je v angleški in nemški literaturi. Verjetno smo slovenci podedovali prvega iz časov skupne države, le da bi bili drugačni od drugih. Kot še marsikje drugje.Eh, mnogi tako razmišljate, pa vsi narobe. To je podobno, kot čevlji in metri. Njuna uporabnost je odvisna od narave problema, ki ga poskušamo rešiti:
Spherical coordinate system @ Wikipedia
Geographic coordinate system @ Wikipedia
one too many ::
Kot je rekel @jype.
Lambda = Phi (azimut)
Phi = Theta - 90° (polarni kot)
Pri prvem primeru je izhodišče za polarni kot (phi) ekvator pri drugem primeru pa z os (theta).
Torej prvič je geografski koordinatni sistem, drugič pa sferični.
Lambda = Phi (azimut)
Phi = Theta - 90° (polarni kot)
Pri prvem primeru je izhodišče za polarni kot (phi) ekvator pri drugem primeru pa z os (theta).
Torej prvič je geografski koordinatni sistem, drugič pa sferični.
primoz4p ::
Se mi zdi, da manjka v zgornjih enačbah kakšen minus (za polno transformacijo pa tudi preslikava Y in Z koordinate ter pri tem se tretji kot)
Skratka:
prvi zapis je zapis z Tait-Bryan koti
drugi zapis pa z Euler koti
Google -> wikipedia (Euler angles @ Wikipedia
Copy-paste
"The second type of formalism is called Tait-Bryan angles, after Peter Guthrie Tait and George H. Bryan. It is the convention normally used for aerospace applications, so that zero degrees elevation represents the horizontal attitude. Tait-Bryan angles represent the orientation of the aircraft with respect to the world frame. When dealing with other vehicles, different axes conventions are possible."
Skratka:
prvi zapis je zapis z Tait-Bryan koti
drugi zapis pa z Euler koti
Google -> wikipedia (Euler angles @ Wikipedia
Copy-paste
"The second type of formalism is called Tait-Bryan angles, after Peter Guthrie Tait and George H. Bryan. It is the convention normally used for aerospace applications, so that zero degrees elevation represents the horizontal attitude. Tait-Bryan angles represent the orientation of the aircraft with respect to the world frame. When dealing with other vehicles, different axes conventions are possible."
primoz4p ::
Laična razlaga pa je taka:
Na eni strani imamo Eulerja, ki je fiksiral koordinatni sistem (globalni koordinatni sistem; kartezičen in polarni zapis)
Na drugi strani pa so "egoistični" Lagrange ("vzel s seboj" kartezičen - ga fiksiral na materialno točko) in "egoistična" Tait in Bryan (ki sta fiksirala polarni zapis na materialno točko (letalo))
Jaz se ne strinjam, da se te "egoistične" zapise ukine. Za mene so v določenih primerih zelo uporabni; v drugih pa je seveda boljše uporabiti Eulerjev zapis.
Na eni strani imamo Eulerja, ki je fiksiral koordinatni sistem (globalni koordinatni sistem; kartezičen in polarni zapis)
Na drugi strani pa so "egoistični" Lagrange ("vzel s seboj" kartezičen - ga fiksiral na materialno točko) in "egoistična" Tait in Bryan (ki sta fiksirala polarni zapis na materialno točko (letalo))
Jaz se ne strinjam, da se te "egoistične" zapise ukine. Za mene so v določenih primerih zelo uporabni; v drugih pa je seveda boljše uporabiti Eulerjev zapis.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Kako je definirana zemljepisna širina/višina: na krogli ali elipsoidu (WGS)?Oddelek: Znanost in tehnologija | 3330 (2566) | LuiIII |
| » | Polarni zapis kompleksnega številaOddelek: Šola | 5805 (5116) | Wolfman |
| » | Trigonometrične enačbeOddelek: Šola | 3320 (2894) | ta_ki_tke |
| » | E (matematična konstanta) (strani: 1 2 3 4 )Oddelek: Šola | 17050 (11514) | Jst |
| » | Razdalja med kroglo in stožcemOddelek: Programiranje | 3401 (2728) | jernejl |