Forum » Programiranje » Razdalja med kroglo in stožcem
Razdalja med kroglo in stožcem
snow ::
Gruntam algoritem za izračun razdalje med kroglo in stožcem. In pa ki je pravokoten na površino in kaže do krogle. Kakšna ideja kdo?
Random mutation plus nonrandom cumulative natural selection - Richard Dawkins

gruntfürmich ::
=x*1
"Namreč, da gre ta družba počasi v norost in da je vse, kar mi gledamo,
visoko organizirana bebavost, do podrobnosti izdelana idiotija."
Psiholog HUBERT POŽARNIK, v Oni, o smiselnosti moderne družbe...
visoko organizirana bebavost, do podrobnosti izdelana idiotija."
Psiholog HUBERT POŽARNIK, v Oni, o smiselnosti moderne družbe...
DJ ::
Jst imam idejo!
Najprej se strezni ;) nato pa napiši razločno in logično kaj hočeš! :D
P.S.
Očitno ga mladina preveč pije hehe pol se pa pojavljajo takšni šoki :D hehe :D
Najprej se strezni ;) nato pa napiši razločno in logično kaj hočeš! :D
P.S.
Očitno ga mladina preveč pije hehe pol se pa pojavljajo takšni šoki :D hehe :D
ROTpantER
darkkk ::
kako misliš "je stožec pravokoten na kroglo" in "kaže na kroglo"?
Zdaj če gre os stožca skozi središče krogle je zadeva trivialna. (pač razdalja od plašča krogle do vrha stožca)...
Če os stožca ne gre skozi središče krogle imaš pač problem, ker je čisto odvisno do katere točke na stožcu bi ti meril, pa katero razdaljo. Mogoče razmisli, da bi izračunal razdaljo od središča krogle to premice, ki je os stožca, nato pa še od točke na tej premici, ki je najbližje krogli do vrha stožca. (in imaš potem direkt razdaljo iz pitagorovega izreka)
Kot so se že pred mano izjasnili, definiraj problem bolje.
Zdaj če gre os stožca skozi središče krogle je zadeva trivialna. (pač razdalja od plašča krogle do vrha stožca)...
Če os stožca ne gre skozi središče krogle imaš pač problem, ker je čisto odvisno do katere točke na stožcu bi ti meril, pa katero razdaljo. Mogoče razmisli, da bi izračunal razdaljo od središča krogle to premice, ki je os stožca, nato pa še od točke na tej premici, ki je najbližje krogli do vrha stožca. (in imaš potem direkt razdaljo iz pitagorovega izreka)
Kot so se že pred mano izjasnili, definiraj problem bolje.
BlackHole ::
Jaz mislim, da je razdalja, torej ta daljica, pravokotna na površino krogle in hkrati na površino stožca. Ampak stožec ima spodaj eno ravno ploskev. NE vem no.
LP Marko

gruntfürmich ::
to je verjetno neke vrste igra: on neki bluzi, mi pa ugotavljamo kaj je v resnici mislu (če je res kaj)

"Namreč, da gre ta družba počasi v norost in da je vse, kar mi gledamo,
visoko organizirana bebavost, do podrobnosti izdelana idiotija."
Psiholog HUBERT POŽARNIK, v Oni, o smiselnosti moderne družbe...
visoko organizirana bebavost, do podrobnosti izdelana idiotija."
Psiholog HUBERT POŽARNIK, v Oni, o smiselnosti moderne družbe...
snow ::
Hm tam manjka beseda vektor v prvem postu ;)
Se pravi iščem razdaljo med plaščem stožca in (površino) kroglo.
Rad bi pa tudi imel vektor, ki je pravokoten na plašč stožca in gre skozi središče krogle.
Se pravi iščem razdaljo med plaščem stožca in (površino) kroglo.
Rad bi pa tudi imel vektor, ki je pravokoten na plašč stožca in gre skozi središče krogle.
Random mutation plus nonrandom cumulative natural selection - Richard Dawkins

WarpedGone ::
Hmm, tole je bolj kot problem algoritma problem klasične algebre. Zahakli kazga matematika. Če je vreden svojga naziva bi ti moral zdrdrat formule.
Zbogom in hvala za vse ribe
darkkk ::
Mjah.. matematik pravi:
problem še vedno slabo definiran.
Npr:
00
00 00
00 00
00
00
0000
0000
00
Kje ima sedaj stožec vektor pravokoten na plašč(oz. osnovno ploskev) skozi središče? Kaj je tu razdalja?
Zdaj lahko malo domnevamo ali pa poizkušamo problem rešiti v malo manj splošni lepoti:
npr:
-vzameš ravnino, kateri je os stožca normala in gre skozi središče krogle, ter daljico na tej ravnini(od središča krogle do premice skozi os) definiraš za razdaljo.
-zahtevaš, da gre pravokotnica iz neke fiksno določene točke na plašču(če je na osnovni ploskvi je trivialno) skozi središče krogle. Potem pač dobiš pravokotni vektor z vektorskim produktom vektorja od "roba(kjer se stika plašč in osnovna ploskev) do vrha" stožca ter vektorjem, ki je tangenten na pravokotni presek stožca
Pač mislim si, da bi rad spackal neko kroženje stožca okoli krogle(sicer morda napačna tema?) Če to, potem imaš v npr. rešitev.
Drugače pa matematik inside tukaj, samo tole je malo preslabo definiran problem, v vsej svoji splošni lepoti pač ne obstaja neka splošna formula.
p.s. forum uničil sliko
problem še vedno slabo definiran.
Npr:
00
00 00
00 00
00
00
0000
0000
00
Kje ima sedaj stožec vektor pravokoten na plašč(oz. osnovno ploskev) skozi središče? Kaj je tu razdalja?
Zdaj lahko malo domnevamo ali pa poizkušamo problem rešiti v malo manj splošni lepoti:
npr:
-vzameš ravnino, kateri je os stožca normala in gre skozi središče krogle, ter daljico na tej ravnini(od središča krogle do premice skozi os) definiraš za razdaljo.
-zahtevaš, da gre pravokotnica iz neke fiksno določene točke na plašču(če je na osnovni ploskvi je trivialno) skozi središče krogle. Potem pač dobiš pravokotni vektor z vektorskim produktom vektorja od "roba(kjer se stika plašč in osnovna ploskev) do vrha" stožca ter vektorjem, ki je tangenten na pravokotni presek stožca
Pač mislim si, da bi rad spackal neko kroženje stožca okoli krogle(sicer morda napačna tema?) Če to, potem imaš v npr. rešitev.
Drugače pa matematik inside tukaj, samo tole je malo preslabo definiran problem, v vsej svoji splošni lepoti pač ne obstaja neka splošna formula.
p.s. forum uničil sliko
Zgodovina sprememb…
- spremenil: darkkk ()
ikslm ::
vektor_pravokoten_na_plašč_stožca = center_spodnje_stranice_stozca-center_krogle
d = vektor_pravokoten_na_plašč_stožca.length()-(visina_stozca+polmer_krogle)
d = vektor_pravokoten_na_plašč_stožca.length()-(visina_stozca+polmer_krogle)
snow ::
Študiram nekaj v tej smeri, ki jo je predstavil darkkk. Hvala!
Pišem simulacijo gibanja delcev (krogel), ki bi jih rad spuščal po liju (sestavljen iz stožca in valja). Kot podatke, ki jih potrebujem za preračun trkov med delci in steno pa rabim 'overlap' med steno lija (stožca/valja) in delcem (kroglo). Pri tem potrebujem tudi kot oziroma pravokotni vektor na ravnino trka.
> vektor_pravokoten_na_plašč_stožca = center_spodnje_stranice_stozca-center_krogle
Tole je ziher?
Pišem simulacijo gibanja delcev (krogel), ki bi jih rad spuščal po liju (sestavljen iz stožca in valja). Kot podatke, ki jih potrebujem za preračun trkov med delci in steno pa rabim 'overlap' med steno lija (stožca/valja) in delcem (kroglo). Pri tem potrebujem tudi kot oziroma pravokotni vektor na ravnino trka.
> vektor_pravokoten_na_plašč_stožca = center_spodnje_stranice_stozca-center_krogle
Tole je ziher?
Random mutation plus nonrandom cumulative natural selection - Richard Dawkins
darkkk ::
vektor_pravokoten_na_plašč_stožca = center_spodnje_stranice_stozca-center_krogle
Tole je ziher?
NE! Vektorji pravokotni na osnovno ploskev stožca so vsi enako usmerjeni(pač vsak je normala one osnovne ploskve), pač samo vzameš onega ki gre skozi središče krogle(ni pa nujno da tak obstaja... pač predstavljaj si kroglo nad stožcem).
Oni vektorji iz plašča stožca so pa bolj tricky. Daj ti sliko nariši, magari v slikarju pa postaj nekam pa daj link, mogoče bom lahko kaj pomagal.
ikslm ::
Jaz sem napisal rešitev za najlažji primer (vektor iz vrha stožca, glede na to da je usmerjen proti krogli, proti središču krogle). Boljše rešitve trenutno ni možno podati, ker je problem zelo slabo opisan.
darkkk ::
Jaz sem napisal rešitev za najlažji primer (vektor iz vrha stožca, glede na to da je usmerjen proti krogli, proti središču krogle). Boljše rešitve trenutno ni možno podati, ker je problem zelo slabo opisan.
Aja to je bila ta razdalja. Samo vektorja pravokotnega na ploskev tam nima :/
jernejl ::
Morda si mislil takole:
Če pogledamo na zadevo od zgoraj (tloris), vidimo v projekciji dva kroga (eden je projekcija stožca, drugi pa projekcija krogle).
Označimo lahko razdaljo med središčem projekcije stožca in središčem projekcije krogle z d.
Če pogledamo od strani, ima stožec obliko trikotnika. Krogla (v projekciji je to krog), je na višini h od vrha stožca oz. trikotnika, ter pomaknjena za razdaljo d v levo ali desno.
Potem je razdalja, ki je pravokotna na stranico trikotnika in gre skozi središče kroga, enaka
x = h sin(alpha) - d cos(alpha).
(če se nisem kje zmotil)
Alpha je polovični kot v vrhu trikotnika.
Minimalna razdalja med kroglo in stožcem je potem za radij manjša od x.
Če pogledamo na zadevo od zgoraj (tloris), vidimo v projekciji dva kroga (eden je projekcija stožca, drugi pa projekcija krogle).
Označimo lahko razdaljo med središčem projekcije stožca in središčem projekcije krogle z d.
Če pogledamo od strani, ima stožec obliko trikotnika. Krogla (v projekciji je to krog), je na višini h od vrha stožca oz. trikotnika, ter pomaknjena za razdaljo d v levo ali desno.
Potem je razdalja, ki je pravokotna na stranico trikotnika in gre skozi središče kroga, enaka
x = h sin(alpha) - d cos(alpha).
(če se nisem kje zmotil)
Alpha je polovični kot v vrhu trikotnika.
Minimalna razdalja med kroglo in stožcem je potem za radij manjša od x.
snow ::
Se bom potrudil, da bo bolj razumljivo.
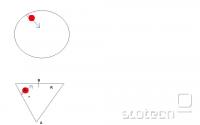
Imamo stožec z vrhom A in točko B, ki predstavlja središče osnovne plošče stožca z radijem R.
Nekje v prostoru pa se nahaja tudi krogla z radijem r in središčem C.
Iščemo pa tisti modri vektor na sliki in dolžino od stene stožca do stene/središča krogle.
Zdaj z ravnino ABC , ki gre skozi točke A, B in C ter vektorjem AB lahko določimo še dve točki (recimo R1 in R2), ki prav tako ležita na ravnini ABC in sta od točke B oddaljeni za R.
Tako imamo na tej ravnini ABC en trikotnik in en krog... če je to res kaj sem do sedaj pisal?
Potem pa gledam razdalje med središčem kroga in stranicami trikotnika?
In s pomočjo enačbe 3 na http://mathworld.wolfram.com/Point-Line... določujem tudi točko, ki je pravokotna na stranico.
Je to vredu tudi za mejne primere, ker krog(la) ni točka...?
Random mutation plus nonrandom cumulative natural selection - Richard Dawkins
Zgodovina sprememb…
- zavarovalo slike: snow ()
jernejl ::
Jaz sem pa mislil takole:
Za ta primer velja:
x = h sin(alpha) - d cos(alpha).
x je torej razdalja od središča kroga do stranice trikotnika,
x - radij_kroga pa je razdalja, ki jo iščeš.
x je skalar (razdalja), če želiš iz tega dobiti vektor, poiščeš še dva kota (fi in theta) za sferični koordinatni sistem.
Glej tudi wiki sferični koordinatni sistem
theta = 90°- alpha
fi pa dobiš, če opazuješ tloris (iz središča krogle in stožca).
Razdaljo x, theta in fi lahko potem s pomočjo enačb (link wiki) pretvoriš v kartezični koord. sistem.
Za ta primer velja:
x = h sin(alpha) - d cos(alpha).
x je torej razdalja od središča kroga do stranice trikotnika,
x - radij_kroga pa je razdalja, ki jo iščeš.
x je skalar (razdalja), če želiš iz tega dobiti vektor, poiščeš še dva kota (fi in theta) za sferični koordinatni sistem.
Glej tudi wiki sferični koordinatni sistem
theta = 90°- alpha
fi pa dobiš, če opazuješ tloris (iz središča krogle in stožca).
Razdaljo x, theta in fi lahko potem s pomočjo enačb (link wiki) pretvoriš v kartezični koord. sistem.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | matematika, geometrije v ravnini, telesaOddelek: Šola | 3661 (3030) | manniac |
| » | Izpeljava volumna krogelnega odseka brez uporabe integriranjaOddelek: Šola | 4226 (1219) | Math Freak |
| » | matematika - kako se izračunaOddelek: Šola | 3203 (2485) | amigo_no1 |
| » | Aproksimacija krogaOddelek: Šola | 2539 (2158) | whatever |
| » | opisna geometrijaOddelek: Šola | 3314 (3129) | Urc |