Forum » Šola » Fourierjeva vrsta, fourierjeva transformacija
Fourierjeva vrsta, fourierjeva transformacija
slovencl ::
Fourierjeva vrsta sem ugotovil kaj je, ni mi pa jasno, kakšno povezavo ima s fourierjevao transformacijo? Mogoče kdo ve?
A. Smith ::
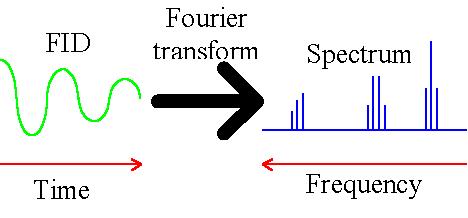
Fourierjeva transformacija je integralska transformacija, ki transformiranko prestavi iz časovnega v frekvenčni prostor.
Transformiranka je praviloma enačba ali nek računski izraz.
Fourierjeve vrste pa samo prevedejo neko funkcijo na nekem območju na vsoto sinusov in (ali) kosinusov.
Transformiranka je praviloma enačba ali nek računski izraz.
Fourierjeve vrste pa samo prevedejo neko funkcijo na nekem območju na vsoto sinusov in (ali) kosinusov.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
mktech ::
heh, a ni da ko tole vsoto kosinusov ali sinusov sestejes/integriras ("nekje v limiti") dobis fourierovo transformiranko?

gruntfürmich ::
sj nektire formule so podobne, sam gre za različna pojma. torej lahko rečemo da je povezava v podobnih/enakih formulah.
"Namreč, da gre ta družba počasi v norost in da je vse, kar mi gledamo,
visoko organizirana bebavost, do podrobnosti izdelana idiotija."
Psiholog HUBERT POŽARNIK, v Oni, o smiselnosti moderne družbe...
visoko organizirana bebavost, do podrobnosti izdelana idiotija."
Psiholog HUBERT POŽARNIK, v Oni, o smiselnosti moderne družbe...
rasta ::
S Fourierovo vrsto se opisuje periodične signale, katerih frekvenčna funkcija je časovno zvezna.
Ko pa gre perioda proti neskončnosti, da se dobimo Fourierov integral. Takrat je tudi Frekvenčna funkcija zvezna in pri vseh frekvencah enaka 0. V tem primeru se zato gleda amplitudno gostoto v odvisnosti od frekvenc.
Ko pa gre perioda proti neskončnosti, da se dobimo Fourierov integral. Takrat je tudi Frekvenčna funkcija zvezna in pri vseh frekvencah enaka 0. V tem primeru se zato gleda amplitudno gostoto v odvisnosti od frekvenc.
Zgodovina sprememb…
- spremenil: rasta ()
marjan_h ::
Ali mi lahko kdo razloži kaj dobimo po Fourierjevi transformaciji?
Nekje piše da če integriramo od minus neskončno do neskončno, in namesto f vstavimo recimo 10 (10 Hz). Potem dobimo amplitudo ki pove, koliko 10 Hz prisotnih v signalu. Torej dobimo neko število.
Vendar so še tukaj koeficenti, te naj bi dobili po transformaciji. Kako? In kaj sploh predstavljajo koeficenti, ali so to koeficienti polinoma funkcije?
Kaj vrača Matlab?
Hvala za odgovore.
Nekje piše da če integriramo od minus neskončno do neskončno, in namesto f vstavimo recimo 10 (10 Hz). Potem dobimo amplitudo ki pove, koliko 10 Hz prisotnih v signalu. Torej dobimo neko število.
Vendar so še tukaj koeficenti, te naj bi dobili po transformaciji. Kako? In kaj sploh predstavljajo koeficenti, ali so to koeficienti polinoma funkcije?
Kaj vrača Matlab?
Hvala za odgovore.
Smrekar1 ::
Ali mi lahko kdo razloži kaj dobimo po Fourierjevi transformaciji?
Verjetno vam nikoli niso blagovolili povedat zakaj se FT lahko uporablja ane. Pogost problem za razumevanje.
Zgodovina sprememb…
- spremenil: Smrekar1 ()
marjan_h ::
Potrebujem za matematiko, vendar sem zbegan, ker kot sem rekel nekje piše da dobimo koefieciente, nekje je evaluirano z f = 10.
In kaj dobiš v Matlabu?
In kaj dobiš v Matlabu?
čuhalev ::
Potrebno bo razlikovati med Fourierovo transformacijo in Fourierovo vrsto. Če se dobro spomnim.
Transformacija integrabilni fukciji priredi funkcijo.
Vrsta je trigonometrični polinom, ki aproksimira periodično funkcijo.
Transformacija integrabilni fukciji priredi funkcijo.
Vrsta je trigonometrični polinom, ki aproksimira periodično funkcijo.
marjan_h ::
Ja samo, v integralu je med minus neskončno in neskončno. Kar pomeni da jo moraš evaluirati, če prav razumem.
marjan_h ::
Sorry za double post.
Nekdo mi je odgovoril glede tega kar vrača Matlab:
Ne razumem dobro kaj pomeni. Torej ne vrača natanko koeficiente. Pri matlab izpisu dobimo nekaj takega 5 + 7i. Realni del so magnitude imaginarni pa fazni zamik. Ne razumem kako si naj predstavljam fazni zamik v imaginarni enoti.
Ali zna kdo to razložiti? Verjetno fiziki to bolj razumejo.Hvala
Nekdo mi je odgovoril glede tega kar vrača Matlab:
you get a value for each multiple of a base frequency, this base frequency in hz is your sampling rate divided by the length of your signal (fs/n)
Ne razumem dobro kaj pomeni. Torej ne vrača natanko koeficiente. Pri matlab izpisu dobimo nekaj takega 5 + 7i. Realni del so magnitude imaginarni pa fazni zamik. Ne razumem kako si naj predstavljam fazni zamik v imaginarni enoti.
Ali zna kdo to razložiti? Verjetno fiziki to bolj razumejo.Hvala
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Programiranje - prepoznavanje tonovOddelek: Pomoč in nasveti | 2341 (1793) | ginekk |
| » | MatematikaOddelek: Šola | 4179 (2887) | marjan_h |
| » | Kaj pa, če so nevtrini vendarle hitrejši od svetlobe?Oddelek: Novice / Znanost in tehnologija | 10801 (9350) | one too many |
| » | Kako se učiti matematiko na višji ravni (strani: 1 2 )Oddelek: Šola | 14117 (12595) | lebdim |
| » | [Matlab] Fouriereva transformacija in analiza odzivov procesaOddelek: Programiranje | 3085 (2910) | nosk8fx |