Forum » Znanost in tehnologija » enačba elipse
enačba elipse
gzibret ::
Imam eno vprašanje.
Kako bi zapisal enačbo elipse v katezičnem koordinatnem sistemu, ki bi bila zarotirana za poljubno stopinj s centrom rotacije v koordinatnem izhodišču?
Hvala za pomoč.
Kako bi zapisal enačbo elipse v katezičnem koordinatnem sistemu, ki bi bila zarotirana za poljubno stopinj s centrom rotacije v koordinatnem izhodišču?
Hvala za pomoč.
Vse je za neki dobr!
:roketa> ::
x -> x*cos(alfa) - y*sin(alfa)
y -> x*sin(alfa) + y*cos(alfa)
Tako nadomestiš x in y v enačbi za elipso.
Alfa je kot zavrtitve.
y -> x*sin(alfa) + y*cos(alfa)
Tako nadomestiš x in y v enačbi za elipso.
Alfa je kot zavrtitve.
Cofko Cof ::
Predvidevam, da želiš narisat to elipso nekam na zaslon? Ker če je to res, lahko pač izračunaš točke po navadni formuli in potem rotiraš vsako točko posebej kot ti je roketa napisal.
Ars longa,vita brevis.
Zgodovina sprememb…
- spremenil: Cofko Cof ()
gzibret ::
Ja, izris elipse na zaslon je eden od ciljev. Čeprav ni glavni cilj. Poskušam modelirati razprševanje onesnaženja iz točkovnega nepremičnega vira, pa rabim enačbo. Nekako bo ta rešitev, da po izračunu koordinat točk le-te premakneš naknadno nek izhod v skrajni sili, samo način mi ni všeč in je manj uporaben za moj namen.
Vse je za neki dobr!
Cofko Cof ::
Dj mal bolj točno napiš kako naj bi to delal pa kje boš to delov. Ker u Matlabu maš že ful stvari napisanih za te rotacije,...
Ars longa,vita brevis.
gzibret ::
Ja sej, glih to sem mislil. Če je že kaka enačba narejena za namen, ki sem ga opisal. Nekako takole:
y = f(x); pa je noter še kakšen parameter ki pove, koliko je stvar rotirana.
Nebi rad nalagal mathlaba in se mučil z njim zaradi ene enačbe.
Kako - mislim narediti enačbo koncentracije polutanta v odvisnosti od GK koordinat oz. v odvisnosti od razdalje in smeri od onesnaževalca (polarne koordinate ne pridejo u poštev!).
Kje mislim to delati - Excell bo kar zadostoval. Ne rabim več.
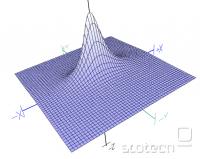
Anomalija izgleda nekako takole, sam bi rad zadevo še malo "sfriziral"
y = f(x); pa je noter še kakšen parameter ki pove, koliko je stvar rotirana.
Nebi rad nalagal mathlaba in se mučil z njim zaradi ene enačbe.
Kako - mislim narediti enačbo koncentracije polutanta v odvisnosti od GK koordinat oz. v odvisnosti od razdalje in smeri od onesnaževalca (polarne koordinate ne pridejo u poštev!).
Kje mislim to delati - Excell bo kar zadostoval. Ne rabim več.
Anomalija izgleda nekako takole, sam bi rad zadevo še malo "sfriziral"
Vse je za neki dobr!
Zgodovina sprememb…
- zavarovalo slike: gzibret ()
SavoKovac ::
Če maš v 3D, potem moraš malce drugače zastavit...
Ako pa samo opisuješ "hribček", je z = f(x,y) najboljši pristop.
Če pa je hudo zapletene narave, potem si izbereš točke z mreže (x,y), recimo velikosti 10x10. Tem stotim točkam določiš z vrednosti na roko, ostale vrednosti pa dobiš z interpolacijo. Linearno, bi-kvadratno...
Primer funkcije: z = a/((x*x+c)*(y*y+d))
Ako pa samo opisuješ "hribček", je z = f(x,y) najboljši pristop.
Če pa je hudo zapletene narave, potem si izbereš točke z mreže (x,y), recimo velikosti 10x10. Tem stotim točkam določiš z vrednosti na roko, ostale vrednosti pa dobiš z interpolacijo. Linearno, bi-kvadratno...
Primer funkcije: z = a/((x*x+c)*(y*y+d))
Zgodovina sprememb…
- spremenil: SavoKovac ()
gzibret ::
Sej enačbo v 3D že imam (z=f(x,y))), vendar ta enačba vključuje tudi enačbo elipse, pa bi jo rad malo zasukal. Sedaj je ta podolgovat hrib orientiran zgolj v -x+x ali -y+y smeri, pa bi rad, da bi ga orientiral poljubno.
> Tem stotim točkam določiš z vrednosti na roko, ostale vrednosti pa dobiš z interpolacijo. Linearno, bi-kvadratno...
To je že narejeno, do mm natančno... Na podlagi realih podatkov (vzorcev). Sedaj bi rad opisal obnašanje onesnaženja z eno enačbo tipa z=f(x,y), kjer bi x in y bile koordinate v kilometrskem (ali metrskem, ni važno) koordinatnem sistemu z izhodiščem v viru onesnaženja.
Na podlagi realih podatkov (vzorcev). Sedaj bi rad opisal obnašanje onesnaženja z eno enačbo tipa z=f(x,y), kjer bi x in y bile koordinate v kilometrskem (ali metrskem, ni važno) koordinatnem sistemu z izhodiščem v viru onesnaženja.
Problem je, ker pri trenurni enačbi (korelacija z realnimi podatki je >0.8) moraš vse točke prej korigirati tako, da je koordinatno izhodišče orientirano skladno z daljšo osjo "elipsaste" anomalije, rad pa bi, da tega ne bi bilo treba prej narediti.
No, to je point.
> Tem stotim točkam določiš z vrednosti na roko, ostale vrednosti pa dobiš z interpolacijo. Linearno, bi-kvadratno...
To je že narejeno, do mm natančno...
Problem je, ker pri trenurni enačbi (korelacija z realnimi podatki je >0.8) moraš vse točke prej korigirati tako, da je koordinatno izhodišče orientirano skladno z daljšo osjo "elipsaste" anomalije, rad pa bi, da tega ne bi bilo treba prej narediti.
No, to je point.
Vse je za neki dobr!
SavoKovac ::
IMHO bi šlo tudi kartezično, če bi odnos med x, y in kotom podal implicitno, samo potem nimaš oblike y=f(x).
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Kot med vektorjemaOddelek: Šola | 3314 (2879) | mirator |
| » | Grrrrr... ta matematikaOddelek: Šola | 1796 (1592) | tasy9 |
| » | Krivulje drugega reda - stožniceOddelek: Šola | 1830 (1594) | KruceFix |
| » | E (matematična konstanta) (strani: 1 2 3 4 )Oddelek: Šola | 17074 (11538) | Jst |
| » | [Fizika] Sile (strani: 1 2 )Oddelek: Šola | 14176 (13265) | seminal |