Forum » Šola » tangenta --> daljica
tangenta --> daljica

BRBR ::
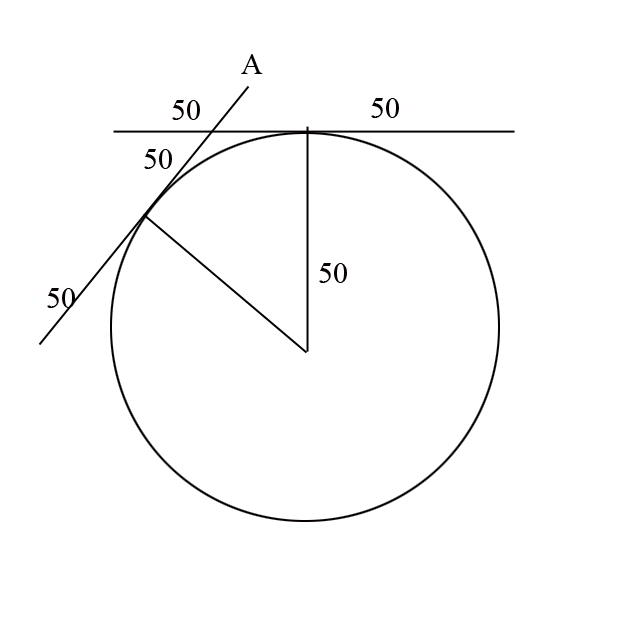
Recimo da imam točko na krožnici x,y , znan je kajpak tudi r. Kao zračunam dve točki na tangenti z dotikališčem v točki x,y, ki sta od dotikališča oddaljeni recimo 50 enot.
Never underestimate the power of idiots in large groups.
- premaknil iz Pomoč in nasveti: bluefish ()
mirator ::
Tangenta je na polmer vedno pravokotna. Če daš koordinate skozi središče kroga, tako da je r na y osi, potem je točka dotikališča tangente (0,r), oddaljena točka od dotikališča pa (50,r).

BRBR ::
Tangenta je na polmer vedno pravokotna. Če daš koordinate skozi središče kroga, tako da je r na y osi, potem je točka dotikališča tangente (0,r), oddaljena točka od dotikališča pa (50,r).
Sicer res, kaj pa za vse vmesne primere, ko r ni na x ali y osi ?
Never underestimate the power of idiots in large groups.

BRBR ::
Never underestimate the power of idiots in large groups.
Zgodovina sprememb…
- spremenil: BRBR ()
mirator ::
Vedno si lahko skico narišeš tako, je koordinatno izhodišče v središču krožnice in r v osi y. Tako pač dobiš koordinate dotikališča in iskane točke. Če to zavrtiš za kot fi, potem dobiš nove koordinate (x' in y'):
x'= x*cos fi +y*sin fi
y'= -x*sin fi + y*cos fi
Seveda moraš najbrž priti do teh enačb sam. Nariši skico, iz točk povleci navpičnice in horizontale na x in y os in iz dobljenih trikotnikov izračunaš nove koordinate. Niti ni tako zahtevno.
x'= x*cos fi +y*sin fi
y'= -x*sin fi + y*cos fi
Seveda moraš najbrž priti do teh enačb sam. Nariši skico, iz točk povleci navpičnice in horizontale na x in y os in iz dobljenih trikotnikov izračunaš nove koordinate. Niti ni tako zahtevno.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Zrcaljenje čez krožnicoOddelek: Šola | 1724 (612) | BRBR |
| » | Trigonometrične enačbeOddelek: Šola | 3326 (2900) | ta_ki_tke |
| » | E (matematična konstanta) (strani: 1 2 3 4 )Oddelek: Šola | 17090 (11554) | Jst |
| » | geometrijska konstrukcijaOddelek: Šola | 4256 (3459) | euler |
| » | Geometrijska konstrukcijaOddelek: Šola | 4706 (4706) | euler |