Forum » Šola » Geometrijska konstrukcija
Geometrijska konstrukcija
euler ::
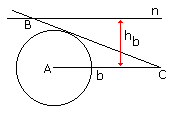
Narisi trikotnik z danimi podatki:
t_b (teziscnica na b)
v_c (visina na c)
r (polmer vcrtane kroznice)
Tuhtam in tuhtam, pa ne gre.
Kaksna ideja?
t_b (teziscnica na b)
v_c (visina na c)
r (polmer vcrtane kroznice)
Tuhtam in tuhtam, pa ne gre.
Kaksna ideja?
sidd ::
tole mi smrdi po opisni geometriji. Rešitve se ne spomnim, se pa splača pogledati za knjigo opisna geometrija prof. Prebila. Zagotovo imajo v knjižnici, na fakulteti (mb in lj) pa 100%.
Gugl pa tud nekaj najde!
lp
p.s.
Pardon, za to ne rabiš kaj dost opisne znat! Začni z včrtano krožnico.
p.p.s.
Thomas, dobra stran!
Gugl pa tud nekaj najde!
lp
p.s.
Pardon, za to ne rabiš kaj dost opisne znat! Začni z včrtano krožnico.
p.p.s.
Thomas, dobra stran!
no idea for signature
signed
I
signed
I
Zgodovina sprememb…
- spremenilo: sidd ()
sidd ::
Že petič popravljam....thomas ti je že dal odgovor, jaz pa kje začet. Malo pomisli, ni težko! Sem pa zbrisal mojo razlago zaradi enostavnosti problema.
lp
lp
no idea for signature
signed
I
signed
I
Zgodovina sprememb…
- spremenilo: sidd ()
euler ::
sidd, morda sem res butelj, ampak ne znam. Tudi zate ne verjamem, da znaš. V nasprotno me boš prepričal samo tako, da boš napisal rešitev.
sidd ::
Pa sem imel upanje da boš sam pogruntal.
Včrtana krožnica
iz središča nekam potegni težiščnico na b
Skozi prosti konec težiščnice potegni tangenti na obe strani kroga (nekakšna 2 kraka enakostraničnega trikotnika na tem delu)
Potem pa glede na en krak potegni vzporednico oddaljeno za višino na c, in kjer se seka ta vzporednica z drugim krakom, tam je točka c recimo.
Ostane še samo povezava ogljišč c in a.
Če ne bo šlo, malo poglej link od thomasa
Če pa še tako ne bo šlo, pa ti narišem pa skeniram, samo dvomim da danes.
Sem pa res upal da boš sam pogruntal - zadeva ni težka. Pa ne gre se za to če si butelj ali ne. Odvisno je samo koliko si vložil časa v to, druga ni važno :)
lp
Včrtana krožnica
iz središča nekam potegni težiščnico na b
Skozi prosti konec težiščnice potegni tangenti na obe strani kroga (nekakšna 2 kraka enakostraničnega trikotnika na tem delu)
Potem pa glede na en krak potegni vzporednico oddaljeno za višino na c, in kjer se seka ta vzporednica z drugim krakom, tam je točka c recimo.
Ostane še samo povezava ogljišč c in a.
Če ne bo šlo, malo poglej link od thomasa
Če pa še tako ne bo šlo, pa ti narišem pa skeniram, samo dvomim da danes.
Sem pa res upal da boš sam pogruntal - zadeva ni težka. Pa ne gre se za to če si butelj ali ne. Odvisno je samo koliko si vložil časa v to, druga ni važno :)
lp
no idea for signature
signed
I
signed
I
euler ::
Ne razumem tvoje rešitve. A si lahko bolj natančen (korak za korakom)?
Ni treba risat skice, samo da točno poveš korake.
Ni treba risat skice, samo da točno poveš korake.
euler ::
Po tvoji konstrukciji je središče včrtane krožnice od točke B oddaljeno za t_b, kar je narobe.
Ice-Heki ::
Pogruntat je treba samo v kakšnem odnosu sta stranica in polmer ... btw: v katerem letniku maš tole nalogo?
euler ::
Če bi rad številke, evo jih: t_b=9, v_c=5, r=2.
Ali ga res ni junaka, ki bi znal rešiti srednješolsko nalogo?
Ali ga res ni junaka, ki bi znal rešiti srednješolsko nalogo?
Thomas ::
Eh, dej že nehej. Nobenmu se ne ljubi reševat tegale problema ene par ur skp! Kar pa ne pomeni, da ne bi marsikdo znal.
Če ni nikjer nobene spletne strani, kjer bi bile za vse teoretično možne podane inpute narejena konstrukcija trikotnika, pa tud poden!
Če je tebi toliko do tega, potem pa reši vse te osnovnošolske naloge konstrukcij trikotnikov in jih daj nekam na net! Potem lahko tržiš oglasni prostor!
Če ni nikjer nobene spletne strani, kjer bi bile za vse teoretično možne podane inpute narejena konstrukcija trikotnika, pa tud poden!
Če je tebi toliko do tega, potem pa reši vse te osnovnošolske naloge konstrukcij trikotnikov in jih daj nekam na net! Potem lahko tržiš oglasni prostor!
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Ja, čist sprejemam kritiko.
Ne vem, kaj mi je blo. Sicer je res, kar sem povedal, da je sramota za cel svet, ker ni sajta z vsemi teoretično možnimi konstrukcijami trikotnikov ... ampak zakaj je pa ne bi poskusili narest!?
Eulerjev primer rešimo, skompiliramo druge že znane, kot je recimo tista, ko so podane vse tri stranice ... in to je to. Sajt z vsemi rešinimi problemi konstrikcije trikotnika.
p.s.
Se pa ne bi ni pretirano čudil, če kakšna od teh konstrukcij sploh še ni narejena.
Ne vem, kaj mi je blo. Sicer je res, kar sem povedal, da je sramota za cel svet, ker ni sajta z vsemi teoretično možnimi konstrukcijami trikotnikov ... ampak zakaj je pa ne bi poskusili narest!?
Eulerjev primer rešimo, skompiliramo druge že znane, kot je recimo tista, ko so podane vse tri stranice ... in to je to. Sajt z vsemi rešinimi problemi konstrikcije trikotnika.
p.s.
Se pa ne bi ni pretirano čudil, če kakšna od teh konstrukcij sploh še ni narejena.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Ja, more bit! Trije podatki so vedno dovolj, da narišeš trikotnik.
At least, I've been told so. Nekej časa me je begalo, zakaj pa ni dobro, če izvemo vse tri kote. Kakšno sekundo. Potem se mi je posvetilo, da če zveš tri kote, si zvedel samo dva kota, tretjega pa izračunaš tako ali tako. Dva podatka sta pa premalo.
Samo tole je off topic.
Torej če zveš tri podatke ki so medsebojno neizpeljivi, lahko načrtaš trikotnik. Enolično.
Najprej za vajo izračunajmo, koliko je sploh teh kombinacij, kako je naloga lahko zadana! Bistveno različnih, seveda. a, b in višna na c je ista kot a, c in višina na b.
At least, I've been told so. Nekej časa me je begalo, zakaj pa ni dobro, če izvemo vse tri kote. Kakšno sekundo. Potem se mi je posvetilo, da če zveš tri kote, si zvedel samo dva kota, tretjega pa izračunaš tako ali tako. Dva podatka sta pa premalo.
Samo tole je off topic.
Torej če zveš tri podatke ki so medsebojno neizpeljivi, lahko načrtaš trikotnik. Enolično.
Najprej za vajo izračunajmo, koliko je sploh teh kombinacij, kako je naloga lahko zadana! Bistveno različnih, seveda. a, b in višna na c je ista kot a, c in višina na b.
Man muss immer generalisieren - Carl Jacobi
Ice-Heki ::
Ja, more bit! Trije podatki so vedno dovolj, da narišeš trikotnik.
S tem se strinjam.
At least, I've been told so. Nekej časa me je begalo, zakaj pa ni dobro, če izvemo vse tri kote. Kakšno sekundo. Potem se mi je posvetilo, da če zveš tri kote, si zvedel samo dva kota, tretjega pa izračunaš tako ali tako. Dva podatka sta pa premalo.
Če imaš podane vse 3 kote ne moreš narisati trikotnika - no, narišeš ga lahko, vendar je teh trikotnikov neskončno - sam namreč definiraš kako velik bo s tem ko si izbereš poljubno stranico => podobni trikotniki.
Najprej za vajo izračunajmo, koliko je sploh teh kombinacij, kako je naloga lahko zadana! Bistveno različnih, seveda. a, b in višna na c je ista kot a, c in višina na b
do sedaj sem poznal naslednje naloge:
- a, b, višina na c oz. podobne
- a,b,c => podane vse stranice
- stranici in kot med njima
- stranica, kot nasproti nje in višina
- stranica, težiščnica in višina
- EDIT: pravokotni trikotnik je svoja zgodba
- EDIT: trikotnik v polkrogu pa svoja (ok, je pravokotni vendar se ga konstruira malo drugače)
- hm, mogoče bi se še kakšna našla pa se je sedajle ne spomnim ...
Mi pa ni jasno v kakšni povezavi je polmer kroga z stranico ... Težiščnica namreč ne gre čez središče kroga (če bi to držalo, potem znam narisat ta trikotnik).
Thomas se ti da malo obrazložiti, ker sedaj tudi mene tole zanima
Zgodovina sprememb…
- spremenil: Ice-Heki ()
euler ::
Kar se tiče vprašanja, koliko je možnih konstrukcij, sem o tem že razmišljal.
Omejimo se na naslednji izbor podatkov:
1. a,b,c
2. alfa,beta,gama
3. va,vb,vc (višine)
4. sa,sb,sc (simetrale kotov)
5. ta,tb,tc (težiščnice)
6. R (očrtan krog)
7. r (včrtan)
8. o (obseg)
Iz teh podatkov se da na kar dosti načinov izbrati 3 (na bistveno različne načine, kot je že Thomas rekel).
- Recimo, da izberemo vse tri podatke iz ene od prvih 5 vrstic ....... 5 možnosti
- Izberemo 2 podatka iz ene od 5 vrstic, tretji iz ene druge vrstice ...... 5*3*(4*3+3) možnosti (5=izberemo vrstico z dvema, 3=izberemo par, 4*3+3=izberemo tretji podatek)
- Tri različne vrstice ....... vse tri izmed prvih 5 ..... (5 nad 3)*6 (izberemo 3 vrstice,
podatek v eni vrstici fiksiramo, ostane nam še 6 možnosti)
........ dve izmed prvih 5 ....... (5 nad 2)*2*3
......... ena izmed prvih 5........ 5*3
......... nobena izmed prvih 5 ........ 1
skupaj 366 možnosti (če se kdo znajde iz tega mojega računa, pa tut kapo dol).
Kot je Thomas opozoril, nekatere niso OK, npr. alfa,beta,gama ali alfa,b,vc ali alfa,a,R itd.
Recimo da je realna številka tam nekje okrog 300-400.
Večino rešitev se da rešit analitično (trigonometrična solata). Nastavimo enačbe, malo premetavamo in dobimo klobase iz korenov, potem pa to narišemo. Ponavadi dobimo res neprebavljive klobase (korene, ki jih ne spraviš v eno vrsto zvezka A4), kar potem narišemo. Ampak to NI tisto, kar bi jaz rad.
Najbrž tudi obstaja rešitev (recimo mojega problema), ki uporablja vse mogoče teorije in izreke. Ampak jaz bi rad srednješolsko rešitev.
Večina teh problemčkov (med drugim tudi moj) zna biti kar zabavna, če se jih lotiš iz srednje šole.
Thomas, kakšni pa praviš da bi bili zaslužki s temi oglasnimi prostori?
Omejimo se na naslednji izbor podatkov:
1. a,b,c
2. alfa,beta,gama
3. va,vb,vc (višine)
4. sa,sb,sc (simetrale kotov)
5. ta,tb,tc (težiščnice)
6. R (očrtan krog)
7. r (včrtan)
8. o (obseg)
Iz teh podatkov se da na kar dosti načinov izbrati 3 (na bistveno različne načine, kot je že Thomas rekel).
- Recimo, da izberemo vse tri podatke iz ene od prvih 5 vrstic ....... 5 možnosti
- Izberemo 2 podatka iz ene od 5 vrstic, tretji iz ene druge vrstice ...... 5*3*(4*3+3) možnosti (5=izberemo vrstico z dvema, 3=izberemo par, 4*3+3=izberemo tretji podatek)
- Tri različne vrstice ....... vse tri izmed prvih 5 ..... (5 nad 3)*6 (izberemo 3 vrstice,
podatek v eni vrstici fiksiramo, ostane nam še 6 možnosti)
........ dve izmed prvih 5 ....... (5 nad 2)*2*3
......... ena izmed prvih 5........ 5*3
......... nobena izmed prvih 5 ........ 1
skupaj 366 možnosti (če se kdo znajde iz tega mojega računa, pa tut kapo dol).
Kot je Thomas opozoril, nekatere niso OK, npr. alfa,beta,gama ali alfa,b,vc ali alfa,a,R itd.
Recimo da je realna številka tam nekje okrog 300-400.
Večino rešitev se da rešit analitično (trigonometrična solata). Nastavimo enačbe, malo premetavamo in dobimo klobase iz korenov, potem pa to narišemo. Ponavadi dobimo res neprebavljive klobase (korene, ki jih ne spraviš v eno vrsto zvezka A4), kar potem narišemo. Ampak to NI tisto, kar bi jaz rad.
Najbrž tudi obstaja rešitev (recimo mojega problema), ki uporablja vse mogoče teorije in izreke. Ampak jaz bi rad srednješolsko rešitev.
Večina teh problemčkov (med drugim tudi moj) zna biti kar zabavna, če se jih lotiš iz srednje šole.
Thomas, kakšni pa praviš da bi bili zaslužki s temi oglasnimi prostori?
Zgodovina sprememb…
- spremenil: euler ()
Thomas ::
Jest vem, da so zaslužili že z večjimi neumnostmi kar solidne denarje. Take, da bi v Sloveniji za tabo začeli hoditi novinarji od takoimenovanih "družabnih kronik".
Žal to ni noben garant, da s čim pametnejšim boš pa zaslužil 1/100 toliko.
RAZEN ... IMHO je povpraševanje točno po temle problemu med stotine milijoni šolajočih se precej veliko!
Marsikdo naleti na "podane so 3 težiščnice, nariši trikotnik!" ali kaj temu sličnega in bi prihajali sem gor, kar v lepih množicah. IMO.
Sploh, če bi dodajal potem gor še kakšne druge take reči.
Je za premislit.
Žal to ni noben garant, da s čim pametnejšim boš pa zaslužil 1/100 toliko.
RAZEN ... IMHO je povpraševanje točno po temle problemu med stotine milijoni šolajočih se precej veliko!
Marsikdo naleti na "podane so 3 težiščnice, nariši trikotnik!" ali kaj temu sličnega in bi prihajali sem gor, kar v lepih množicah. IMO.
Sploh, če bi dodajal potem gor še kakšne druge take reči.
Je za premislit.
Man muss immer generalisieren - Carl Jacobi
Ice-Heki ::
@euler: imaš mogoče rešitev tega problema? Npr. podane podatke kako velike so stranice?
Meni tega ne uspe rešiti pa konec :( Poskušal, poskušal ... spraševal kolege (fizike, matematike - nekateri med njimi so tudi profesorji), pa ga nismo uspeli rešiti ...
Ok, vsak je poskušal kakšno uro, potem pa obupal, meni ga pa tudi ne uspe rešiti ...
Tako da ko ugotovite se priporočam za rešitev
Meni tega ne uspe rešiti pa konec :( Poskušal, poskušal ... spraševal kolege (fizike, matematike - nekateri med njimi so tudi profesorji), pa ga nismo uspeli rešiti ...
Ok, vsak je poskušal kakšno uro, potem pa obupal, meni ga pa tudi ne uspe rešiti ...
Tako da ko ugotovite se priporočam za rešitev
Karaya 52 ::
Tudi meni ga ni uspelo rešit. Začnem s stranico c, na njen konec zapičim šestilo in naredim lok (težiščnica). Problem imam samo z krožnico. Le ta je včrtana, torej je na presečišču simetral kotov. Ampak slednjega mi ne uspe pravilno uporabit. Če bi vedel točko v kateri se dotika krožnica daljice c bi šlo... Matr, res me zanima kak se to reši. 
Thomas ::
No, ČE bi se jaz resno lotil tele naloge, potem bi se je lotil takole.
Najprej, ne bi se zapičil v samo navedeno, pač pa v kar vse naloge tega tipa, "konstruiraj trikotnik ...".
Torej, kako bi se lotil?
Naredil bi programsko simulacijo papirja (ekran, ali kakšen večji kos memorije, recimo kvadratna matrika 0 in 1, z robom 10 tisoč. Malenkost za današnji PC) ... potem bi naredil programske simulacije naslednjih reči še:
- potegni premico (skozi točko, skozi dve točki ..)
- izberi točko na premici (nekje na ekranu)
- nariši krog s središčem v neki točki in polmerom r
- nariši pravokotnico na premico skozi točko na njej
- poišči vsa sečišča krogov in premic in jih številči
- ....
Največ kakšni 10 takih funkcij, bi bilo čez glavo dovolj. Potem bi klical neko random zaporedje večih takih funkcij.
Potem bi pa gledal, če kakšne tri točke določajo trikotnik z danimi lastnostmi. Naprimer, da ima stranice take kot so podane (generirane) v problemu.
Če bi pri tem naletel, z različnimi vhodnimi podatki, ustrezajoč trikotnik, bi "dal idejo postopka na printer".
Maybe bi podvrgel še nekoliko evoluciji, s kriterijsko funkcijo - čimmanj strokes. Se reče klicanj zgoraj navedenih funkcij.
Rezultat bi bil "conjecturing" konstrukcije.
LAHKO bi šel še bolj podrobno po geometriji.
To je ena taka "weak AI", primerna danšnjemu času.
Ampak ne grem tega delat, jasno da ne. Bi tačas rajš kar "strong AI", če bi se že odločil roke mazat.
Najprej, ne bi se zapičil v samo navedeno, pač pa v kar vse naloge tega tipa, "konstruiraj trikotnik ...".
Torej, kako bi se lotil?
Naredil bi programsko simulacijo papirja (ekran, ali kakšen večji kos memorije, recimo kvadratna matrika 0 in 1, z robom 10 tisoč. Malenkost za današnji PC) ... potem bi naredil programske simulacije naslednjih reči še:
- potegni premico (skozi točko, skozi dve točki ..)
- izberi točko na premici (nekje na ekranu)
- nariši krog s središčem v neki točki in polmerom r
- nariši pravokotnico na premico skozi točko na njej
- poišči vsa sečišča krogov in premic in jih številči
- ....
Največ kakšni 10 takih funkcij, bi bilo čez glavo dovolj. Potem bi klical neko random zaporedje večih takih funkcij.
Potem bi pa gledal, če kakšne tri točke določajo trikotnik z danimi lastnostmi. Naprimer, da ima stranice take kot so podane (generirane) v problemu.
Če bi pri tem naletel, z različnimi vhodnimi podatki, ustrezajoč trikotnik, bi "dal idejo postopka na printer".
Maybe bi podvrgel še nekoliko evoluciji, s kriterijsko funkcijo - čimmanj strokes. Se reče klicanj zgoraj navedenih funkcij.
Rezultat bi bil "conjecturing" konstrukcije.
LAHKO bi šel še bolj podrobno po geometriji.
To je ena taka "weak AI", primerna danšnjemu času.
Ampak ne grem tega delat, jasno da ne. Bi tačas rajš kar "strong AI", če bi se že odločil roke mazat.
Man muss immer generalisieren - Carl Jacobi
Ice-Heki ::
@Thomas: Če te prav razumem ne veš ravno natančno kako bi narisal ta trikotnik - veš samo, da se ga da? Konstrukcije torej ne veš za dan primer?
mchaber ::
Poskusi s to potjo:
1) nariši dve vzporedni premici, oddaljeni za vc.
2) poljubno na eni izmed njih vzami točko, nariši pravokotnico in proti notranjosti pasu odmeri rv ter nariši krožnico.
3) Nariši premico, ki je enako oddaljeno od obeh iz 1) točke.
4) presek s krožnico ti da dve rešitvi TB1 in TB2, eno za pozitivno in drugo za negativno orientiran trikotnik.
5) Iz TB1 ali TB2 odmeri tb na premici iz prve točke, dobiš 4 rešitve za točko B. Potem iz ene od tehk potegneš tangento na krožnico ter dobiš C ( tukaj nisem siguren ali je takšno risanje tangent dopuščeno?) A točke potem ni težko locirat
1) nariši dve vzporedni premici, oddaljeni za vc.
2) poljubno na eni izmed njih vzami točko, nariši pravokotnico in proti notranjosti pasu odmeri rv ter nariši krožnico.
3) Nariši premico, ki je enako oddaljeno od obeh iz 1) točke.
4) presek s krožnico ti da dve rešitvi TB1 in TB2, eno za pozitivno in drugo za negativno orientiran trikotnik.
5) Iz TB1 ali TB2 odmeri tb na premici iz prve točke, dobiš 4 rešitve za točko B. Potem iz ene od tehk potegneš tangento na krožnico ter dobiš C ( tukaj nisem siguren ali je takšno risanje tangent dopuščeno?) A točke potem ni težko locirat
.
mchaber ::
Verjetno si sam pogruntal že is drugih primerov. Namesto tiste tangente bi bilo bolj pravilno potegniti poltran BS ter ta kot podvojiti.
.
kitzbrado ::
mchaber: v tvoji rešitvi je napačna predpostavka, da je točka, kjer težiščnica seka včrtan krog, tudi točka, kjer se stranica AB dotika kroga. Točka, kjer se AB v resnici dotika kroga je točka, kjer premica, ki razpolovi kot beta, seka AB.
sidd ::
Mi pa ni jasno v kakšni povezavi je polmer kroga z stranico ... Težiščnica namreč ne gre čez središče kroga (če bi to držalo, potem znam narisat ta trikotnik).
Sam naredil isto napako, se oproščam.
@mchaber: tako ne gre, saj ne veš točno kako - sem poizkusil tudi sam že to možnost. Mislil, da je prav, potem pa da ne bi ponovil iste napake, še 1x premislil in pregledal - kitzbrado je razložil za katero napako gre.
Najbolj se mi dopade thomasova ideja. Postavit/sprogramirat osnove, pa dat računalniku naj preračunava možnosti. Pametno.
Bom jutri še vprašal nekaj sošolcev za to nalogo - bomo vidli kako se bo obneslo.
Aja, z mathematico bi se dalo kaj tu pomagat? nisem programer, me samo tako zanima informativno.
no idea for signature
signed
I
signed
I
euler ::
Thomas, tvoja ideja je zanimiva in sem o njej že razmišljal (ne sicer za ta konkreten problem, ampak nasplošno). Enostavno bi naključno generiral črte, točke in krožnice.
Problem je po mojem v tem (zakaj se to ne da narest), da je enostavno preveč možnosti. Recimo vsaka konstrukcija kolikor toliko zahtevna ima vsaj recimo 20 korakov. Sedaj pa ti preštej, koliko je vseh možnih konstrukcij dolžine 20. Po moje ga niračunalnika, ki bi vse te konstrukcije preveril prej kot v 10^n letih, kjer je n vsaj 5.
Naloga ni enostavna. Derekt se ne da rešit, kot smo vsi ugotovili (v stilu: začneš s težičnico, dodaš krožnico potem pa samo še odmeriš višino - to ne gre).
Razmišljal sem v to smer: r je čudna spremenljivka, ampak imamo formulo
p=r*o/2 (o obseg); dodamo p=c*vc/2 in dobimo r*o=c*vc; r in vc poznamo.
Dobimo o/c=(a+b)/c+1=vc/r oziroma (a+b)/c=(vc-r)/r=znano.
Poznamo torej razmerje (a+b)/c.
Strel v prazno?
Problem je po mojem v tem (zakaj se to ne da narest), da je enostavno preveč možnosti. Recimo vsaka konstrukcija kolikor toliko zahtevna ima vsaj recimo 20 korakov. Sedaj pa ti preštej, koliko je vseh možnih konstrukcij dolžine 20. Po moje ga niračunalnika, ki bi vse te konstrukcije preveril prej kot v 10^n letih, kjer je n vsaj 5.
Naloga ni enostavna. Derekt se ne da rešit, kot smo vsi ugotovili (v stilu: začneš s težičnico, dodaš krožnico potem pa samo še odmeriš višino - to ne gre).
Razmišljal sem v to smer: r je čudna spremenljivka, ampak imamo formulo
p=r*o/2 (o obseg); dodamo p=c*vc/2 in dobimo r*o=c*vc; r in vc poznamo.
Dobimo o/c=(a+b)/c+1=vc/r oziroma (a+b)/c=(vc-r)/r=znano.
Poznamo torej razmerje (a+b)/c.
Strel v prazno?
Thomas ::
Obstaja en izrek, po katerem je možna geometrijska konstrukcija s šestilom, če je možna s šestilom in ravnilom. Ravnilo je čisti luxuz.
Tako, da neko zaporedje naslednjih funkcij:
- izberi točko na ravnini (=ekranu)
- nariši iz te točke krog z radijem r
- izberi točko na krožnici
- mogoče še da kakšna varianta kot izberi točko znotraj (zunaj) kroga, a mislim da niti ne
No, s tem inštrumentarijem prideš skozi. To bi bilo možno napisat v Critticallu.
Seveda pa moraš imeti neko kriterijsko funkcijo, da stvar konvergira k rešitvi z minimalnim potrebnim številom korakov.
Ampak zdej mam še prej za rešt tisti HASH function, me eden že en čas sprašuje. Pa še ene par taskov prej.
Tako, da neko zaporedje naslednjih funkcij:
- izberi točko na ravnini (=ekranu)
- nariši iz te točke krog z radijem r
- izberi točko na krožnici
- mogoče še da kakšna varianta kot izberi točko znotraj (zunaj) kroga, a mislim da niti ne
No, s tem inštrumentarijem prideš skozi. To bi bilo možno napisat v Critticallu.
Seveda pa moraš imeti neko kriterijsko funkcijo, da stvar konvergira k rešitvi z minimalnim potrebnim številom korakov.
Ampak zdej mam še prej za rešt tisti HASH function, me eden že en čas sprašuje. Pa še ene par taskov prej.
Man muss immer generalisieren - Carl Jacobi
Genetic ::
Če bi rad številke, evo jih: t_b=9, v_c=5, r=2.
Sorry, nisem prej videl te naloge :)
1. Narisi kroznico K s polmerom r(2)
2. Narisi tangento pc na K (nosilka stranice c)
3. Narisi vzporednico pc' na premico pc, oddaljeno za v_c(5) (pc' - nosilka tocke C), tako da je kroznica K med njima
4. Narisi vzporednico pc'' na premico pc, oddaljeno za v_c/2 (pc'' lezi med pc in pc')
5. Oznaci presecisce med pc'' in K z T (eno od njiju)
6. Narisi kroznico K' s srediscem v T in s polmerom t_b(9)
7. Oznaci presecisce med pc in K' z A (tisto od njiju, da bo kroznica K med T in A)
8. Narisi tangento na K, ki gre skozi tocko A - pb (nosilka stranice b)
9. Oznaci presecisce pb in pc' z C
10. Narisi tangento na K, ki gre skozi tocko C - pa (nosilka stranice a)
11. Oznaci presecisce pa in pc z B.
12 Tocke A,B,C so oglisca iskanega trikotnika
kitzbrado ::
Vsec mi je out of the box razmisljanje, samo mislim, da si se zmotil, in sicer pri koraku, ko si narisal tangento na kroznico skozi A. To je namrec ekvivalentno temu, da narises tangento kar skozi tocko T (saj sta obe tangenti vzporedni), za kar smo ze videli, da je narobe.
Genetic ::
Ne, bo kar v redu. Zmotil sem se v tocki 7, kjer sem tocko poimenoval z A (moral bi jo kot B, saj uporabljam t_b in ne t_a). Ce gres po korakih, bi moral dobiti trikotnik, ki zadosca pogojem.
Se enkrat, popravljena navodila (najboljse, da je pc vzporedna x osi in pod kroznico K, da lahko uporabim pojma levo in desno):
1. Narisi kroznico K s polmerom r(2)
2. Narisi tangento pc na K (nosilka stranice c)
3. Narisi vzporednico pc' na premico pc, oddaljeno za v_c(5) (pc' - nosilka tocke C), tako da je kroznica K med njima
4. Narisi vzporednico pc'' na premico pc, oddaljeno za v_c/2 (pc'' lezi med pc in pc')
5. Oznaci presecisce med pc'' in K z T (levo presecisce)
6. Narisi kroznico K' s srediscem v T in s polmerom t_b(9)
7. Oznaci presecisce med pc in K' z B (tisto od njiju, da bo kroznica K med T in B - desno presecisce)
8. Narisi tangento na K, ki gre skozi tocko B in seka premico pc' - pa (nosilka stranice a)
9. Oznaci presecisce pa in pc' z C
10. Narisi drugo tangento na K (ne ze obstojece pa), ki gre skozi tocko C - pb (nosilka stranice b)
11. Oznaci presecisce pb in pc z A
12 Tocke A,B,C so oglisca iskanega trikotnika
Se enkrat, popravljena navodila (najboljse, da je pc vzporedna x osi in pod kroznico K, da lahko uporabim pojma levo in desno):
1. Narisi kroznico K s polmerom r(2)
2. Narisi tangento pc na K (nosilka stranice c)
3. Narisi vzporednico pc' na premico pc, oddaljeno za v_c(5) (pc' - nosilka tocke C), tako da je kroznica K med njima
4. Narisi vzporednico pc'' na premico pc, oddaljeno za v_c/2 (pc'' lezi med pc in pc')
5. Oznaci presecisce med pc'' in K z T (levo presecisce)
6. Narisi kroznico K' s srediscem v T in s polmerom t_b(9)
7. Oznaci presecisce med pc in K' z B (tisto od njiju, da bo kroznica K med T in B - desno presecisce)
8. Narisi tangento na K, ki gre skozi tocko B in seka premico pc' - pa (nosilka stranice a)
9. Oznaci presecisce pa in pc' z C
10. Narisi drugo tangento na K (ne ze obstojece pa), ki gre skozi tocko C - pb (nosilka stranice b)
11. Oznaci presecisce pb in pc z A
12 Tocke A,B,C so oglisca iskanega trikotnika
qwdl ::
Genetic > 10. Narisi drugo tangento na K (ne ze obstojece pa), ki gre skozi tocko C - pb (nosilka stranice b)
in t_b ne bo več 9...
in t_b ne bo več 9...
euler ::
Genetic, naredi si isto napako kot drugi. Problem je v tem, da dotikalisce vcrtane krožnice
s stranico ni nujno točno na razpolovišču te daljice. Natančno si nariši po tvoji metodi pa boš videl, kje je problem.
Privzamem oznake od Genetica.
Najprej tole: narišemo pc, izberemo B na pc, narišemo pc' in pc'', odmerimo tb iz točke
B in dobimo T na premici pc''.
Zdaj je treba "samo še" potegniti daljico AC skozi T od premice pc do pc', da bo polmer
včrtane krožnice "ravno" r.
Ne gre mi iz glave (a+b)/c. Recimo, da hočemo narisati trikotnik A'BC', ki je podoben našemu trikotniku. Izberemo A' na pc. Treba poiskat "samo še" C'. Nosilka težiščnice na b
BT je tudi nosilka težičnice na b trikotnika A'BC' (ker sta podobna).
Razmerja imajo podobni trikotniki enaka, zato mora biti (a'+b')/c'=(vc-r)/r (a',b',c' stranice trikotnika A'BC'). c' poznamo, torej je a'+b'=(vc-r)/r*c'=znana dolžina=recimo d.
Treba torej dobit C', da bo a'+b'=d (in da bo BT res nosilka težiščnice na b)
Kaj je množica točk, ki izpolni a'+b'=d? Elipsa, gorišči sta točki A' in B. Treba najt točko
C' na tej elipsi, da bo premica BT točno razpolavljala daljico A'C'. Problem je seveda, ker ne znamo risat elips...
s stranico ni nujno točno na razpolovišču te daljice. Natančno si nariši po tvoji metodi pa boš videl, kje je problem.
Privzamem oznake od Genetica.
Najprej tole: narišemo pc, izberemo B na pc, narišemo pc' in pc'', odmerimo tb iz točke
B in dobimo T na premici pc''.
Zdaj je treba "samo še" potegniti daljico AC skozi T od premice pc do pc', da bo polmer
včrtane krožnice "ravno" r.
Ne gre mi iz glave (a+b)/c. Recimo, da hočemo narisati trikotnik A'BC', ki je podoben našemu trikotniku. Izberemo A' na pc. Treba poiskat "samo še" C'. Nosilka težiščnice na b
BT je tudi nosilka težičnice na b trikotnika A'BC' (ker sta podobna).
Razmerja imajo podobni trikotniki enaka, zato mora biti (a'+b')/c'=(vc-r)/r (a',b',c' stranice trikotnika A'BC'). c' poznamo, torej je a'+b'=(vc-r)/r*c'=znana dolžina=recimo d.
Treba torej dobit C', da bo a'+b'=d (in da bo BT res nosilka težiščnice na b)
Kaj je množica točk, ki izpolni a'+b'=d? Elipsa, gorišči sta točki A' in B. Treba najt točko
C' na tej elipsi, da bo premica BT točno razpolavljala daljico A'C'. Problem je seveda, ker ne znamo risat elips...
euler ::
Elipse risat ne znamo, znamo pa recimo narisat središče in obe polosi.
Središče O je v razpolovišču A'B.
Polosi: narišemo simetralo A'B. Iz A' odmerimo d/2 do te simetrale in
dobimo točko Q,
OQ je mala polos.
Velika polos: odmerimo (d-c')/2 levo od točke A' na premici pc in dobimo
P. PO je velika polos.
Naredimo razteg v navpični smeri, ki nam iz te elipse naredi krožnico. Iz
elipse dobimo
krožnico s središčem O in polmerom OP. Krožnico označimo s K. Treba še
pogledat, kam se pri raztegu preslika premica BT. Označimo presek premic
BT in OQ s T'. Treba pogledat, kam se preslika T'.
Odmerimo razdaljo OQ od točke O na daljici PO, označimo točko z D. p
premica skozi
DT'. Potegnemo vzporednico p skozi P; kjer ta vzporednica seka OQ, dobimo
T''.
Premica BT se sedaj slika v premico BT''. Zdej treba določit točko M na
krožnici K, tako
da premica BT'' razpolavlja daljico PM. Zrcalimo P čez premico BT'',
narišemo vzporednico
premici BT'' skozi to točko. Kjer ta vzporednica seka krožnico K, je točka
M (sta dve presečišči, izberemo eno od njih). Zdej treba M nazaj raztegnit (v resnici stisnit navpično komponento):
M' projekcija M na OQ, M'' presečišče daljice OQ z vzporednico k premici M'P skozi D.
C' je četrto oglišče pravokotnika MM'M''C'. Trikotnik A'BC' je podoben iskanemu trikotniku.
Potegnemo vzporednico premici A'C' skozi T; kjer ta vzporednica seka premico A'B, je točka A, kjer pa ta vzporednica seka premico C'B,
je točka B. Pa je naloga rešena.
Zgleda da sta dve rešitvi, ker imamo za točko M dve možnosti.
Središče O je v razpolovišču A'B.
Polosi: narišemo simetralo A'B. Iz A' odmerimo d/2 do te simetrale in
dobimo točko Q,
OQ je mala polos.
Velika polos: odmerimo (d-c')/2 levo od točke A' na premici pc in dobimo
P. PO je velika polos.
Naredimo razteg v navpični smeri, ki nam iz te elipse naredi krožnico. Iz
elipse dobimo
krožnico s središčem O in polmerom OP. Krožnico označimo s K. Treba še
pogledat, kam se pri raztegu preslika premica BT. Označimo presek premic
BT in OQ s T'. Treba pogledat, kam se preslika T'.
Odmerimo razdaljo OQ od točke O na daljici PO, označimo točko z D. p
premica skozi
DT'. Potegnemo vzporednico p skozi P; kjer ta vzporednica seka OQ, dobimo
T''.
Premica BT se sedaj slika v premico BT''. Zdej treba določit točko M na
krožnici K, tako
da premica BT'' razpolavlja daljico PM. Zrcalimo P čez premico BT'',
narišemo vzporednico
premici BT'' skozi to točko. Kjer ta vzporednica seka krožnico K, je točka
M (sta dve presečišči, izberemo eno od njih). Zdej treba M nazaj raztegnit (v resnici stisnit navpično komponento):
M' projekcija M na OQ, M'' presečišče daljice OQ z vzporednico k premici M'P skozi D.
C' je četrto oglišče pravokotnika MM'M''C'. Trikotnik A'BC' je podoben iskanemu trikotniku.
Potegnemo vzporednico premici A'C' skozi T; kjer ta vzporednica seka premico A'B, je točka A, kjer pa ta vzporednica seka premico C'B,
je točka B. Pa je naloga rešena.
Zgleda da sta dve rešitvi, ker imamo za točko M dve možnosti.
Vili.Čar ::
Tudi meni s šestilom in ravnilom ni uspelo. K sreči je zadeva v modelirniku bolj enostavna - izgleda, da sta za podane podatke res dve rešitvi:
Zgodovina sprememb…
- spremenilo: Vili.Čar ()
euler ::
Bom dal še outofthebox:
1. pc poljubna premica (recimo vodoravna) in pc' vzporednica k premici pc v oddaljenosti vc, pc'' pa vzporednica v oddaljenosti vc/2, ki je vmes med pc in pc'.
2. Izberemo točko B na premici pc. Krožnica s središčem v B in polmerom tb seka premico pc'' v točki T.
3. Izberemo točko A' na premici pc, ki je levo od B. Označimo s c' razdaljo med A' in B.
4. Narišemo simetralo daljice A'B in jo označimo s p. Točka O je razpolovišče daljice A'B.
5. Točka U je presečišče krožnice s središčem v O in polmerom r s premico p (tisto presečišče, ki je pod O).
6. Točka U' je presečišče krožnice s središčem v U in polmerom vc s premico p (tisto, ki je nad O).
7. Točka V je presečišče kroga s polmerom r in središčem O s premico pc (recimo levo od O).
8. Točka V' je presečišče kroga s polmerom c' in središčem O s premico pc (tisto presečišče, ki je levo od O).
9. Z je presečišče vzporednice k premici U'V skozi točko V' s premico p. Označimo d=|OZ|.
10. Q je presečišče krožnice s središčem A' in polmerom d/2 s premico p.
11. Z' presečišče krožnice s središčem O in polmerom c' s premico p (tisto presečišče, ki je pod O). Z'' razpolovišče daljice Z'Z.
12. P presečišče krožnice s središčem A' in polmerom |OZ''| s premico vc (tisto, ki je levo od A').
13. Q' presečišče krožnice s središčem O in polmerom |OQ| s premico vc (tisto, ki je med P in O).
14. T' presečišče premic BT in p.
15. T'' presečišče vzporednice k premici Q'T' skozi P s premico p. q je premica skozi B in T''. K je krožnica s središčem O in polmerom |OP|.
16. Zrcalimo A' čez q, dobimo A''. q' je vzporednica k premici q skozi A''.
17. M je eno od presečišč premice q' in krožnice K. Na tem mestu dobimo dve rešitvi (dve možnosti za M).
18. M' pravokotna projekcija M na premico p. M'' presečišče vzporednice k premici M'P skozi Q s premico p.
19. M', M'', M so tri oglišča pravokotnica. Četrto označimo s C'.
20. Potegnemo vzporednico k premici A'C' skozi T - ta vzporednica seka premico pc v točki A in premico pc' v točki C.
Če ima kdo kakšno orodje na računalniku, da preveri rešitev. Ker na roke pride lahko precej nenatančno glede na dolžino rešitve.
ps: v prejšnjem postu sem naredil eno napakco: namesto točke P bi moral zrcaliti čez premico točko A', tako kot sem tukaj napisal.
1. pc poljubna premica (recimo vodoravna) in pc' vzporednica k premici pc v oddaljenosti vc, pc'' pa vzporednica v oddaljenosti vc/2, ki je vmes med pc in pc'.
2. Izberemo točko B na premici pc. Krožnica s središčem v B in polmerom tb seka premico pc'' v točki T.
3. Izberemo točko A' na premici pc, ki je levo od B. Označimo s c' razdaljo med A' in B.
4. Narišemo simetralo daljice A'B in jo označimo s p. Točka O je razpolovišče daljice A'B.
5. Točka U je presečišče krožnice s središčem v O in polmerom r s premico p (tisto presečišče, ki je pod O).
6. Točka U' je presečišče krožnice s središčem v U in polmerom vc s premico p (tisto, ki je nad O).
7. Točka V je presečišče kroga s polmerom r in središčem O s premico pc (recimo levo od O).
8. Točka V' je presečišče kroga s polmerom c' in središčem O s premico pc (tisto presečišče, ki je levo od O).
9. Z je presečišče vzporednice k premici U'V skozi točko V' s premico p. Označimo d=|OZ|.
10. Q je presečišče krožnice s središčem A' in polmerom d/2 s premico p.
11. Z' presečišče krožnice s središčem O in polmerom c' s premico p (tisto presečišče, ki je pod O). Z'' razpolovišče daljice Z'Z.
12. P presečišče krožnice s središčem A' in polmerom |OZ''| s premico vc (tisto, ki je levo od A').
13. Q' presečišče krožnice s središčem O in polmerom |OQ| s premico vc (tisto, ki je med P in O).
14. T' presečišče premic BT in p.
15. T'' presečišče vzporednice k premici Q'T' skozi P s premico p. q je premica skozi B in T''. K je krožnica s središčem O in polmerom |OP|.
16. Zrcalimo A' čez q, dobimo A''. q' je vzporednica k premici q skozi A''.
17. M je eno od presečišč premice q' in krožnice K. Na tem mestu dobimo dve rešitvi (dve možnosti za M).
18. M' pravokotna projekcija M na premico p. M'' presečišče vzporednice k premici M'P skozi Q s premico p.
19. M', M'', M so tri oglišča pravokotnica. Četrto označimo s C'.
20. Potegnemo vzporednico k premici A'C' skozi T - ta vzporednica seka premico pc v točki A in premico pc' v točki C.
Če ima kdo kakšno orodje na računalniku, da preveri rešitev. Ker na roke pride lahko precej nenatančno glede na dolžino rešitve.
ps: v prejšnjem postu sem naredil eno napakco: namesto točke P bi moral zrcaliti čez premico točko A', tako kot sem tukaj napisal.
Vili.Čar ::
9. Z je presečišče vzporednice k premici U'V skozi točko V' s premico p. Označimo d=|OZ|.9.
V tem primeru je točka Z enaka U.
V tem primeru je točka Z enaka U.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Načrtovanje trikotnika(nujno)Oddelek: Šola | 4983 (4731) | euler |
| » | Trikotnik-Resljiv ali neresljiv?Oddelek: Šola | 1970 (1634) | cucolino |
| » | Trigonometrične enačbeOddelek: Šola | 3321 (2895) | ta_ki_tke |
| » | geometrijska konstrukcijaOddelek: Šola | 4246 (3449) | euler |
| » | paralelogram !! (strani: 1 2 )Oddelek: Šola | 7609 (6860) | korenje_ver2 |