Forum » Šola » Diferencialna enačba - razpolovna doba
Diferencialna enačba - razpolovna doba
lara2 ::
Pozdrav,
zanima me, kako se iz te navadne diferencialne enačbe vidi, da se razpolovi npr. število atomov skozi čas?
Verjetno bo nekdo rekel, da je potrebno rešiti enačbo, kjer je rešitev Ce^-t. In iz tega se vidi potem eksponentno upadanje. To je res, vendar kako je nekdo sploh prišel do tega diferencialnega nastavka?
hvala, lp lara.
zanima me, kako se iz te navadne diferencialne enačbe vidi, da se razpolovi npr. število atomov skozi čas?
Verjetno bo nekdo rekel, da je potrebno rešiti enačbo, kjer je rešitev Ce^-t. In iz tega se vidi potem eksponentno upadanje. To je res, vendar kako je nekdo sploh prišel do tega diferencialnega nastavka?
hvala, lp lara.
FrRoSt ::
Enačba ti samo pravi: Sprememba št. delcev N na/po spremembo/i časa dt je enako minus faktor lambda, pomnožen z začetnim ševilom delcev N!
Zadevo so pač uporabljali ekperimentalno..... Različne (radioaktivne) zadeve imajo različne čase razpada.
Najpogosteje se uporablja razpolovni čas, to je čas, ki ga snov potrebuje, da razpade polovico njene snovi/mase, .... v nadaljni razpolovni dobi pa še polovico od polovice, se pravi 1 /4, .... in tako dalje.
Zadevo so pač uporabljali ekperimentalno..... Različne (radioaktivne) zadeve imajo različne čase razpada.
Najpogosteje se uporablja razpolovni čas, to je čas, ki ga snov potrebuje, da razpade polovico njene snovi/mase, .... v nadaljni razpolovni dobi pa še polovico od polovice, se pravi 1 /4, .... in tako dalje.
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
Jarno ::
Pretvori v ekvivalentno eksponentno funkcijo, recimo N(t) = N0*e-labmda*t
Potem dobiš eksponentno enačbo, v kateri namesto N(t) vstaviš 1/2 od N0 in izračunaš t.
Potem dobiš eksponentno enačbo, v kateri namesto N(t) vstaviš 1/2 od N0 in izračunaš t.
#65W!
Zgodovina sprememb…
- spremenil: Jarno ()
lara2 ::
Hvala vsem, mislim pa, da je Frost poskušal razložiti kar jaz dobro ne razumem.
Npr. da se znebimo minusa in lambde, potem nam ostane začetno število delcev na desni strani in začetno število delcev na čas na levi. Za poenostavitev si izberemo N = 1000 delcev in zamenjamo infinitezimalno majhen čas na normalnega, torej:
1000/t = 1000
Kaj nam to pove? Sedaj je naklon pozitiven, torej bomo povečali naš kupček atomov. Torej začnemo s 1000 atomi in po času t imamo 1000 atomov. Ne razumem čisto dobro.
hvala, lp lara.
Npr. da se znebimo minusa in lambde, potem nam ostane začetno število delcev na desni strani in začetno število delcev na čas na levi. Za poenostavitev si izberemo N = 1000 delcev in zamenjamo infinitezimalno majhen čas na normalnega, torej:
1000/t = 1000
Kaj nam to pove? Sedaj je naklon pozitiven, torej bomo povečali naš kupček atomov. Torej začnemo s 1000 atomi in po času t imamo 1000 atomov. Ne razumem čisto dobro.
hvala, lp lara.
Jarno ::
V tem primeru gre za stabilen izotop oz. spojino. 
Če imaš 1000 atomov in po nekem "nemajhnem" času spet 1000 atomov.
Razpolovna doba pomeni, koliko časa je potrebno, da ti skupek 1000 atomov razpade in ostane 500 atomov.
V enakem času potem 500 atomov "izpuhti" v 250 atomov itd.
Na povezavi, ki jo je podal reeves, imaš lepo razloženo z enačbami.
Če imaš 1000 atomov in po nekem "nemajhnem" času spet 1000 atomov.Razpolovna doba pomeni, koliko časa je potrebno, da ti skupek 1000 atomov razpade in ostane 500 atomov.
V enakem času potem 500 atomov "izpuhti" v 250 atomov itd.
Na povezavi, ki jo je podal reeves, imaš lepo razloženo z enačbami.
#65W!
lara2 ::
Hvala, vendar nisem mislila tega.
Zanima me kako deluje diferencialna enačba. Glede atomske fizike mi je jasno (izotopi, atomi). Najbolj ne razumem tega, kako ta nastavek iz diferencialne enačbe deluje, torej opis diferencialne enačbe. Zato sem preprosto lambdo in minus pred njo odmislila in sprašujem sedaj po mnogo preprostejši enačbi.
lp, lara.
Zanima me kako deluje diferencialna enačba. Glede atomske fizike mi je jasno (izotopi, atomi). Najbolj ne razumem tega, kako ta nastavek iz diferencialne enačbe deluje, torej opis diferencialne enačbe. Zato sem preprosto lambdo in minus pred njo odmislila in sprašujem sedaj po mnogo preprostejši enačbi.
lp, lara.
Jarno ::
Diferencialno enačbo lahko tudi rešiš, ker sam N ni konstanta, ampak funkcija t-ja, katero potem izračunaš.
Zgornja enačba ti pove zgolj to, da če N(t) odvajaš/diferenciiraš po t-ju, dobiš -lambda * N(t).
Reševanje diferencialnih enačb je posebno poglavje višje matematike in če še tega niste jemali, potem je pač težava v tem.
Zgornja enačba ti pove zgolj to, da če N(t) odvajaš/diferenciiraš po t-ju, dobiš -lambda * N(t).
Reševanje diferencialnih enačb je posebno poglavje višje matematike in če še tega niste jemali, potem je pač težava v tem.
#65W!
Unilseptij ::
Diferencialna enačba "deluje" tako, da imaš na levi strani spremembo količine (v tem primeru število razpadlih atomov) v določenem času, na desni pa količino samo, pomnoženo z nekim faktorjem. To v praksi pomeni, da je sprememba količine sorazmerna količini sami (predznak minus kaže, da se število zmanjšuje s časom). Če je vrednost količine ob času 1 enaka X, potem bo v času 2 enaka 2*X (sprememba količine je enaka količini sami... za lambda=1), ob času 3 bo enaka 4*x (2*X + 2*X) in v času 4 8*X (4*X + 4*X). To je eksponentna krivulja in zato ni presenetljivo, da se to uporabi kot nastavek.
Sicer pa se tako diferencialno enaćbo da rešiti tudi brez uporabe nastavka, po metodi ločitve spremenljivk.
Sicer pa se tako diferencialno enaćbo da rešiti tudi brez uporabe nastavka, po metodi ločitve spremenljivk.
Randomness ::
Najbolj ne razumem tega, kako ta nastavek iz diferencialne enačbe deluje, torej opis diferencialne enačbe. Zato sem preprosto lambdo in minus pred njo odmislila in sprašujem sedaj po mnogo preprostejši enačbi.Zamisli si (biološko) celico, ki se prvi dan razdeli v dve celici. Vsaka izmed teh dveh celic se po enem dnevu spet razdeli v dve novi celici. In tako v nedogled ... To lahko zapišeš kot: Δn=n(i+1)-n(i)=n(i). Enačba pravi, da bo dnevi prirastek števila celic enak številu celic na tisti dan. Število celic bo torej naraščalo po eksponentni krivulji: 1, 2, 4, 8, 16, 32, ...
FrRoSt ::
Hvala vsem, mislim pa, da je Frost poskušal razložiti kar jaz dobro ne razumem.
Npr. da se znebimo minusa in lambde, potem nam ostane začetno število delcev na desni strani in začetno število delcev na čas na levi. Za poenostavitev si izberemo N = 1000 delcev in zamenjamo infinitezimalno majhen čas na normalnega, torej:
1000/t = 1000
Kaj nam to pove? Sedaj je naklon pozitiven, torej bomo povečali naš kupček atomov. Torej začnemo s 1000 atomi in po času t imamo 1000 atomov. Ne razumem čisto dobro.
hvala, lp lara.
NE!!
Vtem tvojem primeru naklon ni pozitiven!! (ČE BI BIL, BI SE ŠT. DELCEV POVEČEVALO!!
ampak je konstanten in je enak 1!! Snov se OHRANJA! LOČITI PA MORAŠ, KAJ JE VEČ OD 1 IN KAJ JE MANJ OD 1!! SAJ GRE TUKAJ ZA PRODUKT!!!!!!Minus je člen, ki ga dobiš iz enačbe in ga ne moreš zanemariti ali nevtralizirati!!
Razumeti moraš in znati brati in pisati matematične formule in zapise!! To ni noben bav bav, potrebuje pa nekaj časa, truda in vaje!!
Zato se moraš vrniti nazaj k definiciji diferenciala in to počasi prehodit in prebavit.
---------------------
Sprememba, diferencial, kakor d ali delta, 4 velika črka grške abecede, .... tudi RAZLIKA po domače, je vedno neka razdalja med dvema točkama!!
V tvojem primeru N1 število delcev ob času t1, (nekateri to označujejo z 0, se pravi N0 in t0, kar pomeni začetno stanje!!) in (poljubnim) sosednim stanjem, ki ga označimo z N2 in t2!
Enačba zgoraj bi se torej nekako zapisala takole:
(N1-N2)/(t1-t2)=neznanka, nekaj, kar se išče, recimo x!!
Števec N1-N2 je negativen, saj delci razpadajo in se število manjša, imenovalec dt pa je pozitiven!
Zdaj pa lahko v to enačbo vpišeš, kakor matematični preprosteži obvladajo, namesto N2 vpišeš lambdaN1, kjer je lambda črka grške abecede in je rezervirana za lasnost snovi!! in je konstanta oz. Snovna konstanta in jo je potrebno za vsako snov poiskati in določiti posebno!!
Kaj dobiš potem!???
Dobiš samo št. Delcev N, haktor lambda in časovno enoto! Enačbo urediš. Če pa vzameš še posebni primer razpolovne dobe, je pa še posebno primerna.... tu pač vzameš: N1/2=N2
Zadeva sama se prebere takole: sprememba, diferencial št. Delcev N na(v) spremembi (diferenciala) časa enaka: minus lambda N!
Minus ti pove, da se št. delcev zmanjša, lambda pa je koeficent (radioaktivne) snovi, ki bi moral biti manjši od 1, če se ne motim!!!
Vsa enačba je seveda odvisna od (spremembe) časa, torej časovnega intervala, ... in če vzameš razpolovno dobo, dobiš samo poseben primer... ki se mu reče razpolovna doba.
Lambda se določa eksperimentalno, za vsako (radioaktivno) snov posebej.
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
lara2 ::
Načeloma znam reševati enostavne diferencialne enačbe, vendar še vedno ne razumem dobro njen opis. Rešitev diferencialne enačbe je funkcija. Pri tej enostavni diferencialni enačbi sprašujemo, katera je ta funkcija N(t), ko jo odvajamo po t dobimo nazaj N(t).
To je vse lepo in prav. Vendar je Frost napisal da je N začetno število delcev. Če si izberemo začetno število delcev N = 1000, potem dN/dt = N, če vstavimo v desno stran N, jo moramo tudi na levo stran. Torej d1000/dt = 1000. Kje točno je tukaj konstanta in kakšen produkt, kot si napisal Frost:
Rada bi razumela, tako kot so drugi napisali za neke celice oz. atome, vendar s strani diferencialne enačbe. Kar je nekdo napisal, da če začnemo z večjo količino atomov, potem bo tudi sprememba (dt) večja. To razumem. Samo mogoče ne, če si konkretno izberemo N = 1000.
hvala lp lara.
To je vse lepo in prav. Vendar je Frost napisal da je N začetno število delcev. Če si izberemo začetno število delcev N = 1000, potem dN/dt = N, če vstavimo v desno stran N, jo moramo tudi na levo stran. Torej d1000/dt = 1000. Kje točno je tukaj konstanta in kakšen produkt, kot si napisal Frost:
Vtem tvojem primeru naklon ni pozitiven!! (ČE BI BIL, BI SE ŠT. DELCEV POVEČEVALO!!;) ampak je konstanten in je enak 1!! Snov se OHRANJA! LOČITI PA MORAŠ, KAJ JE VEČ OD 1 IN KAJ JE MANJ OD 1!! SAJ GRE TUKAJ ZA PRODUKT!!!!!!
Rada bi razumela, tako kot so drugi napisali za neke celice oz. atome, vendar s strani diferencialne enačbe. Kar je nekdo napisal, da če začnemo z večjo količino atomov, potem bo tudi sprememba (dt) večja. To razumem. Samo mogoče ne, če si konkretno izberemo N = 1000.
hvala lp lara.
Jarno ::
Za začetno vrednost neposredno v tej diferencialni enačbi si ni smiselno izbrati konstante (npr. N = 1000), ker se potem dogajajo nesmisli. Če zapišemo malce drugače, to izpade tako:
(1000)' = -lambda * 1000
Vemo, da je odvod konstante 0.
Dobimo:
0 = -lambda * 1000, sledi, da je lambda enaka 0 in nič drugega.
Pogojno smiselno bi bilo zapisati N(t) = 1000, kjer bi potem pri dani lambdi lahko izračunala t, pri katerem je N(t) = 1000.
Vajo lahko ponoviš tudi tako, da si izbereš N0 oz. začetno število atomov.
To je vedno N(t) = et.
(1000)' = -lambda * 1000
Vemo, da je odvod konstante 0.
Dobimo:
0 = -lambda * 1000, sledi, da je lambda enaka 0 in nič drugega.
Pogojno smiselno bi bilo zapisati N(t) = 1000, kjer bi potem pri dani lambdi lahko izračunala t, pri katerem je N(t) = 1000.
Vajo lahko ponoviš tudi tako, da si izbereš N0 oz. začetno število atomov.
katera je ta funkcija N(t), ko jo odvajamo po t dobimo nazaj N(t).
To je vedno N(t) = et.
#65W!
Zgodovina sprememb…
- spremenil: Jarno ()
Unilseptij ::
Enačbo dN/dt = -k*N lahko zapišeš tudi kot dN/N = -k*dt. To pomeni, da je v nekem (infinitezimalnem) časovnem intervalu relativna sprememba količine N (št. atomov v vzorcu) enaka kar konstanti -k. To pomeni, da vedno razpade enak delež snovi, ne glede na to, kdaj gledamo in koliko je snovi na začetku. Diferencial dN lahko zapišeš kot dN = N'*dt, kjer je N' odvod N po času. Ko to vstaviš zgoraj dobiš N'*dt/N = -k*dt. Od tod sledi N' = -k*N, to pa pomeni, da je odvod funkcije N(t) enak funkciji sami pomnoženi z -k. Edina funkcija, katere odvod je enak funkciji sami, je e^t, oziroma, ker imaš še -k, e^(-k*t), ki je določena do multiplikativne konstante, ki jo dobiš iz začetnih pogojev (N0).
Torej N(t) = N0*e^(-k*t).
Torej N(t) = N0*e^(-k*t).
FrRoSt ::
Načeloma znam reševati enostavne diferencialne enačbe, vendar še vedno ne razumem dobro njen opis. Rešitev diferencialne enačbe je funkcija. Pri tej enostavni diferencialni enačbi sprašujemo, katera je ta funkcija N(t), ko jo odvajamo po t dobimo nazaj N(t).
To je vse lepo in prav. Vendar je Frost napisal da je N začetno število delcev. Če si izberemo začetno število delcev N = 1000, potem dN/dt = N, če vstavimo v desno stran N, jo moramo tudi na levo stran. Torej d1000/dt = 1000. Kje točno je tukaj konstanta in kakšen produkt, kot si napisal Frost:
Vtem tvojem primeru naklon ni pozitiven!! (ČE BI BIL, BI SE ŠT. DELCEV POVEČEVALO!!;) ampak je konstanten in je enak 1!! Snov se OHRANJA! LOČITI PA MORAŠ, KAJ JE VEČ OD 1 IN KAJ JE MANJ OD 1!! SAJ GRE TUKAJ ZA PRODUKT!!!!!!
Rada bi razumela, tako kot so drugi napisali za neke celice oz. atome, vendar s strani diferencialne enačbe. Kar je nekdo napisal, da če začnemo z večjo količino atomov, potem bo tudi sprememba (dt) večja. To razumem. Samo mogoče ne, če si konkretno izberemo N = 1000.
hvala lp lara.
Ne!! Narobe!!!!! Že spet se približuješ problemu iz napačne smeri!! Od zgoraj, namesto od spodaj!!! In še mešaš jabolka in hruške!!
dt ni odvisna od števila delcev(atomov, izotopov ali karkoli ze!!)
dt je neodvisna spremenljivka, kar pomeni, da jo lahko ti POLJUBNO izbereš, se vprvi izbereš tisto, ki te npr.zanima, to je lahko en dan, mesec ali leto, ali pa tisoc let! To nanašaš na vodoravno os, se pravi absciso, tam, kjer je x, sr pravi boš imela 1 dan, 10 dni, 20 dni, 1000 dni, .... itd!
Na y os oziroma ordinato pa nanaša ODVISNO spremenljivko, se pravi število delcev N! Recimo, da jih imaš 100 Milkonov!! To je tam, nekje ZELO VISOKO!!! Potem pa ti delci začnejo razpdati, po neki enačbi Eni malce hitreje, eni zelo hitro, drugi počasneje in drugi spet zelo počasi!!! Odvisno od stabilnosti posameznih delcev. Vendar imajo funkcijo, BERI: KRIVULJO razpada podobno. Ne isto ali enako,ampak podobno!
ZDAJ PA BISTVO!!!!!
Če ti poznaš funkcijo razpada in imaš neko polkubno število teh elementov, lahko jiz označiš z N, ali pa številčno npr. tisoc, lahko izračunaš koliko jih boš še imel čez (POLJUBEN) čas!
To je bistvo!! Diferencialnega zapisa!!!! Če ti poznaš funkcijo in ta usteza pogojem, je zveuna itd...... lahko izračunaš (BERI: DOLOČIŠ!!) szanje za polkubno spremembo čaša!! Za čez en dan ali pa eno leto ali pa za čez 60 sekund ali pa tisoč na miljonto sekund!! Odvisno pač, kakšne enote notri daješ! Lahko daješ sekunde,dneveali pa leta! In še vedno jih lahko med seboj pretvoriš oz zamenjaš vvečje ali manjše!!
Kakor ni pomembno, kolikšno število delcev imaš! Lahko 100, miljon, miljardo in 10 tisoč ali pa N!
Dobro! Še vprašanje: če imaš torej 1000 delcev N inje njihova razpolovna doba 1 leto, koliko delcev boš imela torej čez eno leto?
Potem bomo probali pa rešiti še kalšrn enostaven primer! Če bo šlo....
In ŠE ENKRAT!!!!
Ti moraš imeti funkcijo znano!! Na to funkcijo pa lahko, če seveda ustreza pogojem lahko uporabiš diferencialno orodje, daizveš, kako bo v sosednji tocki.... to je lahko 100metrov ali pa 10 dni, odvisno kaj vzameš za neodvisno spremenljivko in kaj hočeš račutaniti, BERI: te ZANIMA! ALIte sprašujejo.
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
lara2 ::
Frost, sicer nisi odgovoril na mojo vprašanje glede ohranjanja snovi, kjer je konstanta 1? Sicer bom pa jaz odgovorila na tvoje vprašanje in sicer če imamo 1000 delcev in je razpolovna doba 1 leto, jih bo čez 1 leto 500.
Torej, če pravilno razumem moramo imeti funkcijo N(t) in ne samo N, kjer je N neka konstanta. Iščemo takšen t, da je funkcija N(t) = 1000. Vem kaj, da diferencial npr. dN(t)/dt in sicer je to naklon. Vsak odvod po neki funkciji, da drugo funkcijo, ki pove kakšen je naklon v vsaki točki prve funkcije.
lp, lara.
Torej, če pravilno razumem moramo imeti funkcijo N(t) in ne samo N, kjer je N neka konstanta. Iščemo takšen t, da je funkcija N(t) = 1000. Vem kaj, da diferencial npr. dN(t)/dt in sicer je to naklon. Vsak odvod po neki funkciji, da drugo funkcijo, ki pove kakšen je naklon v vsaki točki prve funkcije.
lp, lara.
tikitoki ::
Sej dN/dt je sprememba stevila delcev po casu. CE gres v kksen ucbenik pogledat, sem preprican ,da bo tudi pisalo kako so nastavili in zakaj tako.
Zimonem ::
Zimonem ::
Pa kaj to pomeni? Da je tam knjižnica in ziher nekje piše? Po mojem abervezniškem razmišljanju se model rasti pri radioaktivnem razpadu uporablja zaradi occamove žiletke. za posamezen delec ne morš napovedat kdaj bo razpadel(šibka sila), statistično pa lahko predvidiš. Koliko jih bo. In ostali modeli ne nudijo nobene prednosti. Sama funkcija je pa prej točno osnovna eksponentna(v tem primeru logaritemska) funkcija.
FrRoSt ::
Frost, sicer nisi odgovoril na mojo vprašanje glede ohranjanja snovi, kjer je konstanta 1? Sicer bom pa jaz odgovorila na tvoje vprašanje in sicer če imamo 1000 delcev in je razpolovna doba 1 leto, jih bo čez 1 leto 500.
Torej, če pravilno razumem moramo imeti funkcijo N(t) in ne samo N, kjer je N neka konstanta. Iščemo takšen t, da je funkcija N(t) = 1000. Vem kaj, da diferencial npr. dN(t)/dt in sicer je to naklon. Vsak odvod po neki funkciji, da drugo funkcijo, ki pove kakšen je naklon v vsaki točki prve funkcije.
lp, lara.
Tole sem res pozabil, ker je bilo toliko za napisat! 1 je ENOTA za produkt (množenje)! Enota, matematicna!! Če katerokoli zafevo ppmnožiš z 1, sr zadeva NE spremeni! Ohrani svojo vrednost! Če pomnožiš s katerimkoli št. ki je manjše od 1, dobiš MANJ, če pa pomnožiš s št. Li je večji od ena, dobiš VEČ! Pa četudi samo z 1,0⁰000001! Podobno je s kvocientom (deljenjem), samo tam je obratno!! Če zadevo deliš s št. ki je večje od 1, se ti zmanjša! Če pa deliš s št. ki jr manjše od 1, se ti poveča!!
Zdaj si pa že bližje razumevanju!! Zadevo si moraš samo še narisati na papir, da si boš lažje predstavljala za kaj in kako gre!! Morda kasneje prilepim kakšno sliko diferenciala!!
Ta tvoja enačba niti ni diferencialna! Diterencialne enačbe so enačbe, kjer v enačbi nastopa poleg funkcije f(x) tudi njen odvod f'(x) ali celo drugi odvod, torej f"(x), če je diferencialna enačba drugega reda...
To, kar imaš ti, je samo ZAPIS Enačbe v diferencialni obliki ali z diferencialom! In tako se da zapisati vsaka enačba, če izpolnjuje pogoje zveznosti, odvedljivosti,.... Tudi tiste najbolj enostavne in preproste premice!! Samo tam je zadeva kar 0 ali konstanta!!
Še eenkrat o diferencialu in tvoji formuli!!
N ni konstanta, ampak je (NEKA POLJUBNA) VREDNOST!! Pomembna vrednost, če jo npr. ti iščeš ali potrebuješ!! Drugače pa samo ena izmed točk!!
V tem primeru gre za funkcijo N(t), kakor si zapisala, kar pomeni, da je št. Delcev N odvisno od časa!! Se spreminja po času!! Funkcija je sicer enostavna,
za kar so poskrbeli kar znanstveniki sami! Diferencial ti pravi, POVE!! za koliko se spremeni y, se pravi NEODVISNA SPREMENJIVKA!! v tvojem primeru je to število delcev N, če se odvisna spremenljivka spremeni za DOLOČENO (ali nedoločeno - poljubno vrednost!!
Imaš,ali pa DOLOČIŠ dx, to je (x2-x1) in tebi se prikaže - izračuna!! Koliko je zaradi tega sprememba y, dy! To je (y2-y1)!!
Ti rabiš (POTREBUJEŠ) : FUNKCIJO, znano točko na tej funkciji!! torej x1 in njeno vrednost y1 iz funkcije,..... potem pa lahko iz teh podatkov zracunaš/določiš razdaljo/spremembo y, dy!! Ali obratno!! Iz dy dločiš dx!! Spremenjivki sta povezani preko enačbe!
Če imaš totej ob času t1 1000delcev, lahko izračunaš, koliko jih boš imela čez npr. en zeden, ali pa eno leto!
Tvoja enačba se totej v diferencislni obliki glasi in zapiše:
(N2-N1)/(t2-t1)=-lambda×N1
N1,t1 je zdajšnje stanje; če je t2 jutri, se pravi boš dobila št. N2 delcev jutri! Lambda je snovna konstanta, vsaka snov ima svojo!
Če tukaj vzamemo še kot neki posebni primer, da ti imaš 1000 delcev sedaj, danes, rada pa bi vedela, koliko jih je bilo včeraj, potem dobiš v imenovalcu negativen interval -dt npr.-24ur, kar ti da z minusem na drugi strani enačbe dejansko + in iz tega potem dobiš, da si imela (včeraj, ali v preteklosti) vec delcev!
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
lara2 ::
Frost jaz se ne bi strinjala, da je samo enačba zapisana v diferencialni obliki. To je diferencialna enačba prvega reda. N(t) je funkcija in dN(t)/dt je odvod te funkcije. Hm, zakaj so definirali (y2-y1)/(x2-x1) tako. Torej kot razmerje (kvocient) npr. 2/1, če se premaknemo eno enoto v smeri x in dve enoti v smeri y. Zakaj ne bi računali kota med tangento na funkcijo in x-osjo. Zakaj ravno razmerje med spremembo v y ulomeljeno s spremembo v x?
hvala, lp lara.
hvala, lp lara.
FrRoSt ::
Frost jaz se ne bi strinjala, da je samo enačba zapisana v diferencialni obliki. To je diferencialna enačba prvega reda. N(t) je funkcija in dN(t)/dt je odvod te funkcije. Hm, zakaj so definirali (y2-y1)/(x2-x1) tako. Torej kot razmerje (kvocient) npr. 2/1, če se premaknemo eno enoto v smeri x in dve enoti v smeri y. Zakaj ne bi računali kota med tangento na funkcijo in x-osjo. Zakaj ravno razmerje med spremembo v y ulomeljeno s spremembo v x?
hvala, lp lara.
Saj ta sprememba (y2-y1)/(x2-x1) ti da naklonski kot (funkcije) skozi ti dve točki T(x1,y1) in T(x2,y2) in je enak tangensu kota tangente na x os. In mu rečemo odvod!
Zato je tudi taka definicija!!
In zavzame (lahko) vse možne vrednosti za katere je tg definiran!!
Vendar je zapisana v obliki diferenciala, kar ni nič narobe! Tudi lepo se bere
treba je pa zadevo razumeti in razviti!! Odvoda se nimamo, čeparav je nastavljen na levi strani. Je samo v obliki diferenciala... in to je tisti korak med diferencialom in nadalje med ifetizimalnim računom. Diferencial se ti vedno zapiše v obliki intervala x2-x1 ali y2-y1 ali N2-N1 ali t2- t1!! Skratka, od 2 se vedno odšteje 1! Taka je definicija!
Se ti z zadevo mudi!??
Zgornjo tvojo enačbo razviješ in urediš! Prvo pomnož obe strani enačbe z dt, nato pa še tisti N, ki je v resnici samo N, tako kakor jr y v resnici samo y!, preneseš na levo stran enačbe..... in potem recimo na enačbo ( obe strani) udariš integral....
Kaj torej dobiš in kaj ti to grafično prrdstavlja!??
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
tikitoki ::
Pa kaj to pomeni? Da je tam knjižnica in ziher nekje piše? Po mojem abervezniškem razmišljanju se model rasti pri radioaktivnem razpadu uporablja zaradi occamove žiletke. za posamezen delec ne morš napovedat kdaj bo razpadel(šibka sila), statistično pa lahko predvidiš. Koliko jih bo. In ostali modeli ne nudijo nobene prednosti. Sama funkcija je pa prej točno osnovna eksponentna(v tem primeru logaritemska) funkcija.
Tocno to, kar sem napisal. Imas ucbenike, kjer je zadeva kvalitetno in pravilno razlozena. Brez bluzenja in napak.
Itak ne mores napovedati za posamezen delec. Ne vem kaj nej bi imela ochamova britev s tem.
lara2 ::
Frost, zakaj bi pustili tangens kota, zakaj potem ne izračunamo arctan in dobimo v stopinjah kot?
lp, lara.
lp, lara.
Zimonem ::
Pa kaj to pomeni? Da je tam knjižnica in ziher nekje piše? Po mojem abervezniškem razmišljanju se model rasti pri radioaktivnem razpadu uporablja zaradi occamove žiletke. za posamezen delec ne morš napovedat kdaj bo razpadel(šibka sila), statistično pa lahko predvidiš. Koliko jih bo. In ostali modeli ne nudijo nobene prednosti. Sama funkcija je pa prej točno osnovna eksponentna(v tem primeru logaritemska) funkcija.
Tocno to, kar sem napisal. Imas ucbenike, kjer je zadeva kvalitetno in pravilno razlozena. Brez bluzenja in napak.
Itak ne mores napovedati za posamezen delec. Ne vem kaj nej bi imela ochamova britev s tem.
Da se privzame model rasti kot funkcijo. V bistvu gre pa za preslikavo.
FrRoSt ::
Frost, zakaj bi pustili tangens kota, zakaj potem ne izračunamo arctan in dobimo v stopinjah kot?
lp, lara.
Ker ga ne rabiš!!
Saj ti imaš že ta kot, samo je IMPLICITNO zapisan z dy/dx!! In če je funkcija f(x) zvezno odvedljiva, njen odvod f`(x) je zvezna funkcija, potem imaš ti implicit zapis kota za celotno funkcijo!
In za poljubni točki iz te funkcije zapišeš samo v diferencialni obliki in lahko določiš kot! Na tem sloni zadeva! In to že po definiciji!!
Bi znala zapisati v diferencialni obliki enačbo za raztezanje poljubno dolge palice Železniškega tira) pod vplivom temperature!??? V eni smeri, npr. dolžini!? To je še bolj enostaven primer.... Funkcija je premica, vse ostalo pa je analogno.,,
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
lara2 ::
Frost ostanimo pri tej enačbi.
Torej, če rečemo, da začnemo z 1000 delci in jih imamo čez 1000 sekund le 500, potem to zapišemo:
(N2 - N1) / (t2 - t1) = - lambda*N1
(500 - 1000) / (1000 - 0) = - lambda*1000
Iz tega sicer, lahko izračunamo lambdo, ali je vsaj pravilen zapis s števili?
hvala, lp lara.
Torej, če rečemo, da začnemo z 1000 delci in jih imamo čez 1000 sekund le 500, potem to zapišemo:
(N2 - N1) / (t2 - t1) = - lambda*N1
(500 - 1000) / (1000 - 0) = - lambda*1000
Iz tega sicer, lahko izračunamo lambdo, ali je vsaj pravilen zapis s števili?
hvala, lp lara.
Jarno ::
Samo za informacijo, ne bo šlo. Potrebno je poznati razliko med diferenčnim količnikom in diferencialom.
Diferenčni količnik aproksimira situacijo na linearen način, po "premici".
Rešitev prvotne diferencialne enačbe pa je eksponentna funkcija.
Pri tej snovi se zahteva predvsem tole:
1. konkretna rešitev diferencialne enačbe
2. poznavanje določenih lastnosti dobljene funkcije
3. izračun/izražanje določenih količin glede na vhodne podatke.
Diferencialna enačba ni primerna za neposredno obravnavo problema, ker sploh ne vemo, kakšna bo družina funkcij, ki iz nje izhaja (če je ne rešimo).
V končni fazi to zapišemo takole:
500 = 1000 * e-lambda*1000 in izrazimo lambdo.
Diferenčni količnik aproksimira situacijo na linearen način, po "premici".
Rešitev prvotne diferencialne enačbe pa je eksponentna funkcija.
Pri tej snovi se zahteva predvsem tole:
1. konkretna rešitev diferencialne enačbe
2. poznavanje določenih lastnosti dobljene funkcije
3. izračun/izražanje določenih količin glede na vhodne podatke.
Diferencialna enačba ni primerna za neposredno obravnavo problema, ker sploh ne vemo, kakšna bo družina funkcij, ki iz nje izhaja (če je ne rešimo).
Torej, če rečemo, da začnemo z 1000 delci in jih imamo čez 1000 sekund le 500, potem to zapišemo:
V končni fazi to zapišemo takole:
500 = 1000 * e-lambda*1000 in izrazimo lambdo.
#65W!
Zgodovina sprememb…
- spremenil: Jarno ()
FrRoSt ::
Frost ostanimo pri tej enačbi.
Torej, če rečemo, da začnemo z 1000 delci in jih imamo čez 1000 sekund le 500, potem to zapišemo:
(N2 - N1) / (t2 - t1) = - lambda*N1
(500 - 1000) / (1000 - 0) = - lambda*1000
Iz tega sicer, lahko izračunamo lambdo, ali je vsaj pravilen zapis s števili?
hvala, lp lara.
Ne čisto!
Sem zadevo jaz zameglil oz narobe napisal!! Na desni ni N1! Ampak samo N!
Dejansko gre tukaj za funkcijo N(t), kakor si pravilno zapisala. Št. delcev v odvisnosti od časa!! Leva stran pa je pravilno zapisana, dy oz dN=500-1000 in dt=1000-0, če začneš pri 1000 delcih meriti čas do 1000s (in takrat zabeležiš/izmeriš 500 delcev!
Iz tega potem lahko izračunaš lambdo! SAMO ta lambda ne bo merodajna, ker gre skozi samo ti dve točki!!!! Če bi bila funkcija premica, bi šlo! Ker pa ni, pa ne gre!!!
Ti moraš v tem primeru dejansko narediti več meritev, npr. t1=1000s, t2=2000s, t3=3000s, ..... t10=10000s! In izmeriti (eksperimentalno) št. delcev pri teh vrednostih!!!
Potem (lahko) določiš/narišeš PRVOTNO FUNKCIJO!! N(t)!!
Narisati/določiti to PRVOTNO FUUNKCIJO je vedno prvi korak! V tvojem primeru je to neka modifikacija funkcije 1/ t!! Npr. N(t)=(1/t)+8t+3
Ko to funkcijo poznaš, jo lahko odvajaš po času!
Odvod po času (ponavadi) imenujemo hitrost!
Če odvajamo enačbo poti po času dt dobimo hitrost, (m/s,km/h,....), če pa hitrost še enkrat odvajamo po času dt dobimo pospešek (ali pojemek) in pravimo/ beremo: prirastek hitrosti na časovno enoto! Tukaj imamo čas na kvadrat! Sekunda na kvadrat....
V tvojem primeru gre za hitrost razpada/
zmanjšanja št. delcev. Hitrost se ponacadi označi s v; c je rezervirana za konstanto svetlobne hitrosti...
Zdaj imaš PVOTNO FUNKCIJO 1/t, ki jo moraš odvajati po času, da dobiš hitrost razpada!
Ta odvod paje kar tg(kota alfa)=dN/dt!
Odvod je v tem primetu lnt!! Naj te to ne bega!! Ravno prvotna funkcija, prezrcaljena preko abcise (t)!! Je pač taka funkcija. Tak primer!!
Odvod ti kaźe NAKLONSKI KOT!! tg(kota)=dy/dx
V tvojem primeru dejansko dobiš negativno vrednost, kar pomeni, da hitrost pada! Pada pa tudi število delcev...
Prvo je potrebno dobiti (prvotno) funkcijo, odvod te po casu dt ti pa da hitrost razpada.... To sta dve RAZLIČNI FUNKCIJI, čeprav sta povezano z odvodom...
Če bi morala npr izračunati št. delcev, kar je površina med prvotno funkcijo in abciso t, bi morala enačbo integrirati in bi dobila:
N2-N1=integral(prvotne funkcije) na intervalu od t2 do t1.
Integriranje je obratna operacija kakor odvajanje!
Če ti da integral površino/ploščino pod funkcijo, ti odvod samo pove, kako (hitro/pocasi) se ta površina spremeni, če se premakneš za dx ali dt v tvojem primeru..... koliko in kako se spremeni N oz dN.
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
lara2 ::
Enačba ti samo pravi: Sprememba št. delcev N na/po spremembo/i časa dt je enako minus faktor lambda, pomnožen z začetnim ševilom delcev N!
Sem zadevo jaz zameglil oz narobe napisal!! Na desni ni N1! Ampak samo N!
Zakaj si pa potem na začetku, napisal da je N začetno število delcev? N1 je začetno število delcev, v tem primeru.
lp, lara.
FrRoSt ::
TAKO! To sem zajebal!
In ne pozabi, da je zapis samo splošna oblika!! Vsak izotop ima svojo enačico enačb razpada, vse pa so iz iste skupine krivulj!
Zadeva res ni tako težka za razumeti, se pa skriva nekaj pasti!! In ko rečejo, da se vidi, da je odvod kar e na t ali ln, je to samo neki Znanstveni snobizem! Dejansko pa moraš prehodit celo pot navzgor korak po korak, da razumeš to!
Bi znala zdaj zapisati enačbo raztezanja palice (poljubne dolžine) l v diferencialni obliki!??
In ne pozabi, da je zapis samo splošna oblika!! Vsak izotop ima svojo enačico enačb razpada, vse pa so iz iste skupine krivulj!
Zadeva res ni tako težka za razumeti, se pa skriva nekaj pasti!! In ko rečejo, da se vidi, da je odvod kar e na t ali ln, je to samo neki Znanstveni snobizem! Dejansko pa moraš prehodit celo pot navzgor korak po korak, da razumeš to!
Bi znala zdaj zapisati enačbo raztezanja palice (poljubne dolžine) l v diferencialni obliki!??
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
lara2 ::
@Frost (nisem imela dostopa do spleta, zato pozen odgovor)
l = dolžina palice
T = temperatura
dl/dt = -kT
Sicer pa sedaj razumem ta zapis. Pogledala sem še razlago na spletu, temu se reče angl. slope fields. Dejansko na desni strani enačbe dobimo skalar, zato da potem vidimo kakšen je naklon v določeni točki (seveda, če vnesemo lambda, t za radioaktivni razpad)
lp, lara.
l = dolžina palice
T = temperatura
dl/dt = -kT
Sicer pa sedaj razumem ta zapis. Pogledala sem še razlago na spletu, temu se reče angl. slope fields. Dejansko na desni strani enačbe dobimo skalar, zato da potem vidimo kakšen je naklon v določeni točki (seveda, če vnesemo lambda, t za radioaktivni razpad)
lp, lara.
FrRoSt ::
@Frost (nisem imela dostopa do spleta, zato pozen odgovor)
l = dolžina palice
T = temperatura
dl/dt = -kT
Sicer pa sedaj razumem ta zapis. Pogledala sem še razlago na spletu, temu se reče angl. slope fields. Dejansko na desni strani enačbe dobimo skalar, zato da potem vidimo kakšen je naklon v določeni točki (seveda, če vnesemo lambda, t za radioaktivni razpad)
lp, lara.
Tako! Prebere sesprememba dolžine na spremembo Temperature ....ponavadi je t ...čas, T pa je temperatura!!
Po srednješolsko se ta enačba zapiše, brez diferenciala seveda, takole:
l2-l1= k*l* (T2-T1)
Sprememba dolžine (palice) je enaka dolžini l pomnoženi s koeficientom (snovnim) k in spremembi(razliki) temperature!
Tukaj ti diferencial dT daje predznak, ... to pomeni, ali se palica krči (ohlaja) ali razteza (segreva)! Enačba je tudi premica, kar je še enostavnejše od tvojega primera, saj je odvod premice kar konstanta.....
l.p.
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
FrRoSt ::
Je pravilno tudi, kar sem napisala glede "slope fields" in naklona?
lp, lara.
Ne vem, ker v angleščini tega nikoli nisem študiral, že pri kakšnih profesorjih in podajanju nalog iz drugega faksa so bile malce zagate, ker je vsak uporabljal malce svojo terminologijo/besedoslovje.
Mi smo tole enačbo za spremembo dolžine ob spremembi Temperature pisali brez minusa in tudi tvoja enačba je na wikepediji zapisana brez minusa! Vendar je tvoja enačba SPLOŠNI zapis in ta minus samo povdari, da hitrost (razpada delcev) pada! se zmanjšuje!
Diferencial je vedno realno število, oz. skalar, vsaj v polju dveh spremenljivk, kjer je ena neodvisna. Torej v ravnini, npr. x-y!
Če pa imaš več spremenljivk oz. koordinat, npr. x,y in z, potem pa tukaj diferenciraš enačbo po vsaki posebej, imaš pač tri prirastke! Tako kakor je normalno za prostor.
Nikoli ne pozabi da je tg(kota z absciso) kar enak razmerju (=) diferencialu/KVOCIENTU, se pravi dy/dx! Ta kvocient, ali pa kakor tudi funkcija tg (alfa) zavzame vse vrednosti ob -neskončno do +neskončno! In ker je kotna funkcija je perodična!!
Konico svinčnika postavi v koordinatno izhodišče in ga zavrti okoli izhodišča! V nasprotni smeri urinega kazalca, kar je matematično + smer vrtenja!
In boš videla kako se spreminja y in x od kota, oz. dy/dx! Ko leži svinčnik na abscisi, se pravi koordinati x je zadeva nič, dy-števec je takrat nič, potem se dy počasi veča, pod kotom 45st. ali pi/4 je razmerje dy/dx enako 1, takrat sta oba enaka in je zato kvocient 1, potem pa se pri kotu 90 st. ali pi/2 bliža .....
Če potem na absciso naneseš/napišeš vrednosti za pi, dobiš tako ciklično funkcijo....
http://www2.arnes.si/~mpavle1/mp/trigo_...
tgalfa=dy/dx
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
FrRoSt ::
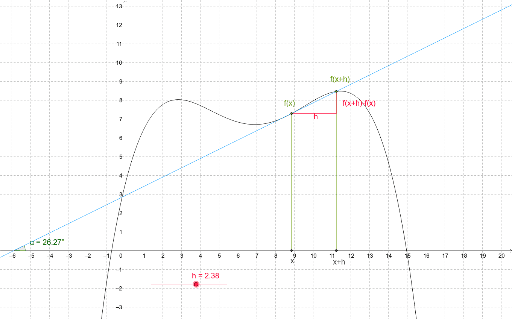
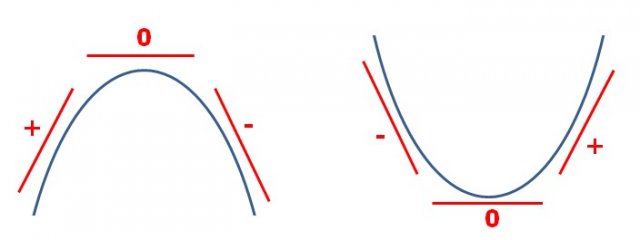
Še nekaj slik, da si morda lažje predstavljaš
Upam, da je kaj ratalo s temi slikami.... Drugače pa sama odtipkaj v google in preglej slike....
l.p.
odvod f.
odvod
odvod - integral (geo-gebra)
funkcija f(x) in kakšna je vrednost njenega odvoda v točki x=1
uporaba odvoda
Upam, da je kaj ratalo s temi slikami.... Drugače pa sama odtipkaj v google in preglej slike....
l.p.
Noben človek ni otok, popolnoma sam zase; smrt slehernega človeka vzame
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
del mene, ker pripadam človeški vrsti; in zato nikdar ne pošiljaj poizvedovat,
komu zvoni; zvoni tebi.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Prehitevanje sinusnih funkcij - smerOddelek: Šola | 1097 (857) | mirator |
| » | [MAT] Diferenciabilnost funkcijeOddelek: Šola | 2679 (1913) | Unilseptij |
| » | prehodni pojaviOddelek: Elektrotehnika in elektronika | 1481 (1119) | stromkekec |
| » | Matematika (stimulacija)Oddelek: Šola | 1837 (1557) | rasta |
| » | E (matematična konstanta) (strani: 1 2 3 4 )Oddelek: Šola | 15807 (10271) | Jst |