Forum » Znanost in tehnologija » Verjetnostne uganke
Verjetnostne uganke
Fizikalko ::
Pa se pejmo kakšne fajne verjetnostne uganke.
Lahko kar začnem. Npr. vlečem kroglice iz vreče biserov. Njih premer je enakomerno razporejen na intervalu med a in b. Iz biserov delam ogrlice. Za vsako ogrlico vlečem bisere toliko časa, da njena dolžina preseže neko dolžino c.Kakšna je verjetnostna porazdelitev ogrlic po številu biserov,, ki so na njih?
He he...
>> Edit: Popravil nalogo, da bo še malo slajša...
Lahko kar začnem. Npr. vlečem kroglice iz vreče biserov. Njih premer je enakomerno razporejen na intervalu med a in b. Iz biserov delam ogrlice. Za vsako ogrlico vlečem bisere toliko časa, da njena dolžina preseže neko dolžino c.Kakšna je verjetnostna porazdelitev ogrlic po številu biserov,, ki so na njih?
He he...
>> Edit: Popravil nalogo, da bo še malo slajša...
- spremenilo: Fizikalko ()
Thomas ::
Zadnjič sem se fino nategnu pr eni enostavni, tlele na forumu. Bom mau vode popil, preden se začnemo igrat tole. :)
Potem bo pa hudo.
Potem bo pa hudo.
Sergio ::
Brez nekega groznega poglabljanja, tako da sem lahko cist popolnoma off. Ne mi zamert.
To zgleda kot navadn Gauss. Normalna porazdelitev.
To zgleda kot navadn Gauss. Normalna porazdelitev.
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
Fizikalko ::
Nisi tako daleč od resnice. Vse je odvisno od izbranih parametrov. He he...
Namig: Če je število konvolucij veliko, je ujemanje verjetnostne porazdelitve po dolžini ogrlice pri fiksnem številu biserov (JA, BREZ TE PORAZDELITVE NE BO ŠLO... ravno zato sem pa nalogco še malo spremenil, da ne bo prelahka...) zelo blizu Gaussa. Problem se pojavi pri majhnem številu konvolucij (biserov) - le nekaj, npr.... Takrat je treba te konvolucije kar izračunat (na roke, he he).
No, pa recimo, da je prejle omenjena porazdelitev Gaussova. Now what?
Namig: Če je število konvolucij veliko, je ujemanje verjetnostne porazdelitve po dolžini ogrlice pri fiksnem številu biserov (JA, BREZ TE PORAZDELITVE NE BO ŠLO... ravno zato sem pa nalogco še malo spremenil, da ne bo prelahka...) zelo blizu Gaussa. Problem se pojavi pri majhnem številu konvolucij (biserov) - le nekaj, npr.... Takrat je treba te konvolucije kar izračunat (na roke, he he).
No, pa recimo, da je prejle omenjena porazdelitev Gaussova. Now what?
Zgodovina sprememb…
- spremenilo: Fizikalko ()
DavidJ ::
Gausova, ce si potegnil vsaj 30 biserov. Ce jih je manj, pitaj boga...
Centralni limitni izrek, ja.
Centralni limitni izrek, ja.
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
Fizikalko ::
Aplavdiram...
Čeprav si malo zgrešil število. Po mojih izračunih se dejanska razhajanja (omembe vredna) pokažejo šele pri okrog 10-15 biserov.
Čeprav si malo zgrešil število. Po mojih izračunih se dejanska razhajanja (omembe vredna) pokažejo šele pri okrog 10-15 biserov.
Zgodovina sprememb…
- spremenilo: Fizikalko ()
Sergio ::
Hehe, ok. Jebenti statistiko, kokrkol obrnes. :)
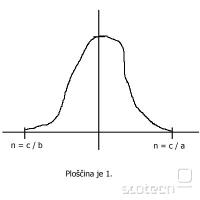
Sicer pa, se enkrat, moje razmisljanje v sliki:
Ni ravno najlepse, ampak mislm da pove point.
Sicer pa, se enkrat, moje razmisljanje v sliki:
Ni ravno najlepse, ampak mislm da pove point.
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
Zgodovina sprememb…
- zavarovalo slike: OwcA ()
Sergio ::
Fizikalko: 30 je (spet sodec po mojem spominu iz predavanj) matematicno precej lepo dokazano stevilo. Mislim da bo 30 kar drzalo, se strinjam z Davidom.
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
Fizikalko ::
>> Sicer pa, se enkrat, moje razmisljanje v sliki:
No, to že (čeprav si pozabil, da gre za diskretno porazdelitev in da je vrh posledično tudi premaknjen), ampak Gauss je zgolj približek. Stvar res GRE proti Gaussu pri velikem številu biserov.
Brez Gaussa je treba delat ročno konvolucije s pomočjo inverzne Fourierove transformacije produkta N Fourierovih transformacij porazdelitve naključnega bisera po premeru (ta porazdelitev je produkt Heavisidovih funkcij).
Če pa dopustimo Gaussa... Kako bi potem zapisali rešitev?
No, to že (čeprav si pozabil, da gre za diskretno porazdelitev in da je vrh posledično tudi premaknjen), ampak Gauss je zgolj približek. Stvar res GRE proti Gaussu pri velikem številu biserov.
Brez Gaussa je treba delat ročno konvolucije s pomočjo inverzne Fourierove transformacije produkta N Fourierovih transformacij porazdelitve naključnega bisera po premeru (ta porazdelitev je produkt Heavisidovih funkcij).
Če pa dopustimo Gaussa... Kako bi potem zapisali rešitev?
Zgodovina sprememb…
- spremenilo: Fizikalko ()
gzibret ::
Jaz bi kej dodal, samo ne razumem dobro naloge 
Naloga se mi v bistvu zdi malo hecna. Ali je kroglic N=trunc (dolžina ogrlice / dolžina bisera) +1 ali pa N+1
Če to delamo mnogo časa pa je porazdelitev odvisna od tega, kilika je razlika med dolžino špage in N*dolžina bisera.
???? A sem prav razumel ?????
Naloga se mi v bistvu zdi malo hecna. Ali je kroglic N=trunc (dolžina ogrlice / dolžina bisera) +1 ali pa N+1
Če to delamo mnogo časa pa je porazdelitev odvisna od tega, kilika je razlika med dolžino špage in N*dolžina bisera.
???? A sem prav razumel ?????
Vse je za neki dobr!
Fizikalko ::
Čakaj, čakaj. Dolžina bisera ni fiksna... Maš pač vrečo biserov, katerih premer je enakomerno porazdeljen na intervalu med a in b. Ni tko simpl. veš...
Zgodovina sprememb…
- spremenilo: Fizikalko ()
Thomas ::
Naloga:
Verjetnost, da je verjetnost dogodka X enaka 1/2 - je 1/2. 1/4 pa je verjetnost, da je verjetnost dogodka X enaka 3/4. 1/8 he verjetnost, da je verjetnost dogodka 7/8 ... itd.
Kako verjeten je dogodek X?
Verjetnost, da je verjetnost dogodka X enaka 1/2 - je 1/2. 1/4 pa je verjetnost, da je verjetnost dogodka X enaka 3/4. 1/8 he verjetnost, da je verjetnost dogodka 7/8 ... itd.
Kako verjeten je dogodek X?
Sergio ::
eps?
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
tsh2 ::
če je 50% verjetnost, da je verjetnost nekega dogodka 50%, potem je verjetnost dogodka 25%. to je sigurno, ne?
potem lahko pretvorimo vprašanje v bolj čisto obliko:
verjetnost dogodka X je:
25%, 19%, 11%, ...
in ta verjetnost se tako enakomerno zmanjšuje.
torej vzamemo povprečje tega zaporedja številk, da dobimo najbolj verjetno verjetnost?
potem lahko pretvorimo vprašanje v bolj čisto obliko:
verjetnost dogodka X je:
25%, 19%, 11%, ...
in ta verjetnost se tako enakomerno zmanjšuje.
torej vzamemo povprečje tega zaporedja številk, da dobimo najbolj verjetno verjetnost?
Double_J ::
1 je verjetnost, da je verjetnost dogodka x 0.
Če je blo mišljeno v nalogi, da je seštevek obeh verjetnosti 1...
Če je blo mišljeno v nalogi, da je seštevek obeh verjetnosti 1...
Zgodovina sprememb…
- spremenil: Double_J ()
Thomas ::
> 1 je verjetnost, da je verjetnost dogodka x 0.
Ne. Vsota vseh verjetnosti, da je verjetnost kolikorže, mora biti enaka 1.
Zato bi nulti člen, ki ga navajaš, ne bi bil legalen.
Ne. Vsota vseh verjetnosti, da je verjetnost kolikorže, mora biti enaka 1.
Zato bi nulti člen, ki ga navajaš, ne bi bil legalen.
Fizikalko ::
Ok, če koga zanima formalizem rešitve moje nalogce (sem mel za domačo nalogo enkrat na faxu, tko da vam sam screenshote PS fajla pokažem):
/kazalo sem spustu, nima veze
/kazalo sem spustu, nima veze
Zgodovina sprememb…
- zavarovalo slike: Fizikalko ()
Fizikalko ::
OK, pa še ena, tokrat iz glave...
Izbiram števila npr. od 1 do 100 (naključno). Kakšna je verjetnost, da bo 10 zaporednih števil (x1, x2, x3,..., x10) takih, da bo x1 > x2 > x3 > x4... ? Lahko seveda tud obrnemo neenačaj, pogoj je pravzaprav le to, da je neko monotono zaporedje.
Se bom zdajle lotil, samo zgleda dosti lažja kot tista prej...
Izbiram števila npr. od 1 do 100 (naključno). Kakšna je verjetnost, da bo 10 zaporednih števil (x1, x2, x3,..., x10) takih, da bo x1 > x2 > x3 > x4... ? Lahko seveda tud obrnemo neenačaj, pogoj je pravzaprav le to, da je neko monotono zaporedje.
Se bom zdajle lotil, samo zgleda dosti lažja kot tista prej...
Fizikalko ::
Ja, sem mel prav, ni tolk zaguljena... Par vrstic dela, nič več. Razen, če sem kaj spregledal.
tsh2 ::
nekam mrtva je ta tema. ali ljudem ni zanimivo, ali pa se bojijo osmešiti. oboje je slabo.
uganke se mi zdijo bistvo znanosti. cela znanost je eno samo reševanje ugank. uganke znajo biti zelo težke, a če se jih lotiš prav in z neko metodo postanejo veliko lažje rešljive.
thomas, kaj je z mojim odgovorom na tvojo uganko?
ta zadnja uganka:
tole je način, da se to uganko reši z logično metodo (moj najljubši način):
poglejmo eno bolj enostavno nalogo:
izberemo tri naključna števila a,b in c izmed 100 števil. kolikšna je verjetnost, da sta drugo in tretje število oba manjša od prvega števila, medsebojno pa je vseeno, v kakšnem razmerju sta: b < a & c < a
sigurno je tole: če izberemo samo dve števili, potem bo verjetnost, da je b < a, 50%.
torej je verjetnost, da drži b < a & c < a: 50%*50%=25%
imamo tri števila, a, b in c. kolikšna je verjetnost, da je c < b < a?
tole mora biti res: b < a & c < a & c < b.
za vsako drži verjetnost 50%. kolikšna je verjetnost, da so vse tri resnične? 50%^3=12.5%
štiri:
b < a & c < a & c < b & d < a & d < b & d < c
50%^6=1.56%
in tako naprej. zgleda, da je verjetnost zelo majhna, tam nekje 0.000...1 %
lahko da sem zgrešil...
naloga se najbrž spremeni, če števila, ki si ga izbral, naslednjič ni več na izbiro v množici za izbirati.
uganke se mi zdijo bistvo znanosti. cela znanost je eno samo reševanje ugank. uganke znajo biti zelo težke, a če se jih lotiš prav in z neko metodo postanejo veliko lažje rešljive.
thomas, kaj je z mojim odgovorom na tvojo uganko?
ta zadnja uganka:
tole je način, da se to uganko reši z logično metodo (moj najljubši način):
poglejmo eno bolj enostavno nalogo:
izberemo tri naključna števila a,b in c izmed 100 števil. kolikšna je verjetnost, da sta drugo in tretje število oba manjša od prvega števila, medsebojno pa je vseeno, v kakšnem razmerju sta: b < a & c < a
sigurno je tole: če izberemo samo dve števili, potem bo verjetnost, da je b < a, 50%.
torej je verjetnost, da drži b < a & c < a: 50%*50%=25%
imamo tri števila, a, b in c. kolikšna je verjetnost, da je c < b < a?
tole mora biti res: b < a & c < a & c < b.
za vsako drži verjetnost 50%. kolikšna je verjetnost, da so vse tri resnične? 50%^3=12.5%
štiri:
b < a & c < a & c < b & d < a & d < b & d < c
50%^6=1.56%
in tako naprej. zgleda, da je verjetnost zelo majhna, tam nekje 0.000...1 %
lahko da sem zgrešil...
naloga se najbrž spremeni, če števila, ki si ga izbral, naslednjič ni več na izbiro v množici za izbirati.
Fizikalko ::
Je pa super, da si poživil temo... me je že mal skrbel. Še Thomas se noče oglasit. Zgleda se nobenemu nič kaj dosti ne da...
Fizikalko ::
Pozabil si namreč odvisnost ene verjetnosti od prejšnje številke. Če je bila izbrana 0.7, potem pač ni 50% verjetnost za naslednjo, itd...
Skratka, obstaja korelacija med njimi.
Skratka, obstaja korelacija med njimi.
Thomas ::
> torej vzamemo povprečje tega zaporedja številk, da dobimo najbolj verjetno verjetnost?
Ne. Vzamemo vsoto.
> Še Thomas se noče oglasit. Zgleda se nobenemu nič kaj dosti ne da...
Jah, mau že pojamra sem pa ke.
Ne. Vzamemo vsoto.
> Še Thomas se noče oglasit. Zgleda se nobenemu nič kaj dosti ne da...
Jah, mau že pojamra sem pa ke.
Thomas ::
Verjetnost, da je verjetnost, da je verjetnost, da je verjetnost ... kakšna je potem verjetnost?
"Rekurzivna verjetnost", bi lahko rekli, je hecna stvar.
Later več o tem.
"Rekurzivna verjetnost", bi lahko rekli, je hecna stvar.
Later več o tem.
CaqKa ::
dva strelca streljata v tarčo. verjetnost da zadane prvi je 2/3 in verjetnost da zadane drugi je 3/4. oba streljata dvakrat. kakšna je verjetnost da sta oba zadela tarčo če je bila zadeta dvakrat?
a to prav razumem da si najprej morem sploh zračunat kakšna je sploh verjetnost da je tarča zadeta dva krat?
a to prav razumem da si najprej morem sploh zračunat kakšna je sploh verjetnost da je tarča zadeta dva krat?
jeti51 ::
Seveda, kaj pa.
Izračunaš verjetnost da je tarčo 2x zadel prvi in hkrati drugi 2x zgrešil.
P20 = 2/3 * 2/3 * 1/4*1/4 = 4/9 * 1/16 = 1/36
Verjetnost, da je tarčo zadel prvi točno enkrat in hkrati drugi točno enkrat (upoštevaj, da vsak izmed njiju lahko zadane tarčo bodisi v prvem, bodisi v drugem poskusu):
P11 = (2/3 * 1/3 + 1/3*2/3) * (3/4*1/4 + 1/4*3/4) = 4/9 * 6/16 = 1/6
Verjetnost, da je tarčo 2x zgrešil prvi in hkrati 2x zadel drugi:
P02 = 1/3*1/3 * 3/4*3/4 = 1/9 * 9/16 = 1/16
To so zdaj vse možnosti, kako je možno točno 2x zadeti tarčo. Poglej, kolikšen delež tega zaseda P11 (da je vsak izmed niju prispeval en zadetek) in to je to. P11 / (P20 + P11 + P02)
Izračunaš verjetnost da je tarčo 2x zadel prvi in hkrati drugi 2x zgrešil.
P20 = 2/3 * 2/3 * 1/4*1/4 = 4/9 * 1/16 = 1/36
Verjetnost, da je tarčo zadel prvi točno enkrat in hkrati drugi točno enkrat (upoštevaj, da vsak izmed njiju lahko zadane tarčo bodisi v prvem, bodisi v drugem poskusu):
P11 = (2/3 * 1/3 + 1/3*2/3) * (3/4*1/4 + 1/4*3/4) = 4/9 * 6/16 = 1/6
Verjetnost, da je tarčo 2x zgrešil prvi in hkrati 2x zadel drugi:
P02 = 1/3*1/3 * 3/4*3/4 = 1/9 * 9/16 = 1/16
To so zdaj vse možnosti, kako je možno točno 2x zadeti tarčo. Poglej, kolikšen delež tega zaseda P11 (da je vsak izmed niju prispeval en zadetek) in to je to. P11 / (P20 + P11 + P02)
DavidJ ::
Ena Italijanska. Na list papirja z ravnimi vzporednimi crtami, razmaknjenimi za a, vrzemo iglo dolzine b. Koliksna je verjetnost, da igla seka katero od crt? 
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
DavidJ ::
Hehe, zgornji primer je samo za zabavo. Ce vas o njem zanima kaj vec, poguglajte za "buffon's needle".
Imam pa zanimivo nalogo.
Do sole je stiri minute hoda. Vmes pa je semafor, na katerem dve minuti gori zelena, dve minuti pa rdeca luc. Od doma se odpravim pet minut pred zacetkom pouka. Kaksna je verjetnost, da pridem se pravocasno?
Niti prevec tezko.
Kaj pa, ce sta semaforja dva?
Boljse.
Imam pa zanimivo nalogo.
Do sole je stiri minute hoda. Vmes pa je semafor, na katerem dve minuti gori zelena, dve minuti pa rdeca luc. Od doma se odpravim pet minut pred zacetkom pouka. Kaksna je verjetnost, da pridem se pravocasno?
Niti prevec tezko.
Kaj pa, ce sta semaforja dva?
Boljse.
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
Azrael ::
Pa še mojih 5 centov.
1. Kolikokrat v povprečju je treba vreči igralno kocko, da bomo dobili vsako cifro vsaj 1x?
In še malo bolj zaguljena, vendar podobna naloga.
Imamo album v katerega lahko nalepimo 100 različnih slčic (nekaj takega, kot je Živalsko kraljestvo). Koliko sličic moramo v povprečju kupiti, da albuim napolnimo?
Koliko sličic pa v povprečju potrebujemo, da taisti album napolnimo z 80. različnimi sličicami?
V obeh primerih predpostavljamo, da je izdelovalec vse sličice izdelal v enakem številu.
1. Kolikokrat v povprečju je treba vreči igralno kocko, da bomo dobili vsako cifro vsaj 1x?
In še malo bolj zaguljena, vendar podobna naloga.
Imamo album v katerega lahko nalepimo 100 različnih slčic (nekaj takega, kot je Živalsko kraljestvo). Koliko sličic moramo v povprečju kupiti, da albuim napolnimo?
Koliko sličic pa v povprečju potrebujemo, da taisti album napolnimo z 80. različnimi sličicami?
V obeh primerih predpostavljamo, da je izdelovalec vse sličice izdelal v enakem številu.
Nekoč je bil Slo-tech.
tsh2 ::
davidj:
poglejmo sigurne stvari:
1. če naletimo na rdečo takrat, ko je prižgana manj kot eno minuto, potem ne bomo prišli pravočasno (1..+4=5..). če pa naletimo na rdečo, ko je prižgana več kot eno minuto, ali na zeleno, potem bomo prišli pravočasno.
2. semafor stoji točno na sredini poti, na mestu x (ni važno, kje točno stoji).
torej moramo biti na mestu x takrat, ko je zelena, ali pa ko je rdeča v svoji drugi polovici.
na mestu x je tako stanje 3/4 časa = 75%.
za dva semaforja pa 9/16 = 56%?
poglejmo sigurne stvari:
1. če naletimo na rdečo takrat, ko je prižgana manj kot eno minuto, potem ne bomo prišli pravočasno (1..+4=5..). če pa naletimo na rdečo, ko je prižgana več kot eno minuto, ali na zeleno, potem bomo prišli pravočasno.
2. semafor stoji točno na sredini poti, na mestu x (ni važno, kje točno stoji).
torej moramo biti na mestu x takrat, ko je zelena, ali pa ko je rdeča v svoji drugi polovici.
na mestu x je tako stanje 3/4 časa = 75%.
za dva semaforja pa 9/16 = 56%?
DavidJ ::
Super!
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
Zgodovina sprememb…
- spremenil: DavidJ ()
Azrael ::
Bom kar podal rešitev:
n = število možnosti (v primerih obeh nalog ploskev kocke ali strani albuma)
p= število ploskev kocke, ki jih želimo videti ali sličic, ki nam manjkajo
Izračunamo tako:
Kar je za primer 6. ploskev kocke enostavno, za 100 sličic v albumu pa relativno zahtevno opravilo.
Formulo lahko zapišemo krajše, vendar je natančnost izračuna manjša (za H10 je rezultat točen na prve 4 cifre, za H100 pa na prvih 6.
Kjer je Hp
γ je Eulerjeva konstanta ~ 0.577215665...
Tako je rešitev za primer metanja kocke
H(6,6) =14.7 metov
Za popolnitev albuma s 100 sličicami je potrebno kupiti
H(100,100) = 519 sličic
Za 80% popolnitev albuma je v povprečju kupiti le:
H(100,100) - H(100,20) = 100 * (H100 - H20) = 159 sličic,
kar je glavni razlog, zakaj večina takih albumov ni nikoli popolnjena do konca.
Vir: Presek V 1977/78, članek Sandokan.
n = število možnosti (v primerih obeh nalog ploskev kocke ali strani albuma)
p= število ploskev kocke, ki jih želimo videti ali sličic, ki nam manjkajo
Izračunamo tako:
H(n,p) = n * (1 + 1/2 + 1/3 + 1/4 + .... + 1/p)
Kar je za primer 6. ploskev kocke enostavno, za 100 sličic v albumu pa relativno zahtevno opravilo.
Formulo lahko zapišemo krajše, vendar je natančnost izračuna manjša (za H10 je rezultat točen na prve 4 cifre, za H100 pa na prvih 6.
H(n,p) = n * Hp
Kjer je Hp
Hp = ln(p + 0.5) + γ
γ je Eulerjeva konstanta ~ 0.577215665...
Tako je rešitev za primer metanja kocke
H(6,6) =14.7 metov
Za popolnitev albuma s 100 sličicami je potrebno kupiti
H(100,100) = 519 sličic
Za 80% popolnitev albuma je v povprečju kupiti le:
H(100,100) - H(100,20) = 100 * (H100 - H20) = 159 sličic,
kar je glavni razlog, zakaj večina takih albumov ni nikoli popolnjena do konca.
Vir: Presek V 1977/78, članek Sandokan.
Nekoč je bil Slo-tech.
tsh2 ::
azrael:
tole je moja nedokončana rešitev uganke metanja kocke, zataknilo se mi je pri eni enostavni stvari.
koliko je verjetnost vsakega meta, da ne bo enak enemu od prejšnjih unikatnih metov?
podproblem: koliko metov povprečno rabimo, da ne vržemo nekega točno določenega števila?
v 1/6 primerov povprečno bomo vrgli to prepovedano število. v 5/6 pa bomo vrgli pravo število.
torej rabimo povprečno koliko metov?
v 6/6 primerov bomo vrgli pravo št: 1
v 1/6 primerov bomo vrgli pravo št: 6
v 50% primerov bomo vrgli pravo št: polovica metov: 3
=podproblem: obstaja verjetnost X, da bo bomo izbrali število A. kolikokrat moramo izbrati povprečno, da bomo dobili A?
saj vem da mora biti enostavno, pa trenutno ne morem pogruntati, kakšna bi bila formula za tole.
kolona1: št. unikatnih metov, ki smo jih že, naredili
kolona2: verjetnost, da met ne bo enak enemu od unikatov
kolona3: št. metov, ki jih povprečno rabimo, da dobimo nov unikat
in potem seštejemo ta števila metov, da dobimo skupno število metov, ki jih rabimo za dosego cilja.
za primer kupovanja sličic pa, ali ni odvisno od tega, koliko sličic je bilo izdelanih? če jih je bilo naprimer izdelanih samo 105, potem je veliko manjša verjetnost, da bomo kupili isto večkrat. razen če predpostavljamo, da obstaja vedno enaka verjetnost za vsako sličico, da jo bomo kupili. tako je v realnosti, ker je zelo veliko sličic.
tole je moja nedokončana rešitev uganke metanja kocke, zataknilo se mi je pri eni enostavni stvari.
koliko je verjetnost vsakega meta, da ne bo enak enemu od prejšnjih unikatnih metov?
podproblem: koliko metov povprečno rabimo, da ne vržemo nekega točno določenega števila?
v 1/6 primerov povprečno bomo vrgli to prepovedano število. v 5/6 pa bomo vrgli pravo število.
torej rabimo povprečno koliko metov?
v 6/6 primerov bomo vrgli pravo št: 1
v 1/6 primerov bomo vrgli pravo št: 6
v 50% primerov bomo vrgli pravo št: polovica metov: 3
=podproblem: obstaja verjetnost X, da bo bomo izbrali število A. kolikokrat moramo izbrati povprečno, da bomo dobili A?
saj vem da mora biti enostavno, pa trenutno ne morem pogruntati, kakšna bi bila formula za tole.
kolona1: št. unikatnih metov, ki smo jih že, naredili
kolona2: verjetnost, da met ne bo enak enemu od unikatov
kolona3: št. metov, ki jih povprečno rabimo, da dobimo nov unikat
kolona1 kolona2 kolona3
0 6/6 1
1 5/6 ?
2 4/6 ?
3 3/6 3
4 2/6 ?
5 1/6 6
in potem seštejemo ta števila metov, da dobimo skupno število metov, ki jih rabimo za dosego cilja.
za primer kupovanja sličic pa, ali ni odvisno od tega, koliko sličic je bilo izdelanih? če jih je bilo naprimer izdelanih samo 105, potem je veliko manjša verjetnost, da bomo kupili isto večkrat. razen če predpostavljamo, da obstaja vedno enaka verjetnost za vsako sličico, da jo bomo kupili. tako je v realnosti, ker je zelo veliko sličic.
Zgodovina sprememb…
- spremenilo: tsh2 ()
Thomas ::
Naslednjega si nisem izmislil sam, le transformiral sem v nekonfuzno obliko.
Agencija javno objavi, da bo metala kocko. Če jim pade 6, bo izžrebala državljana Slovenije in mu poslala milijon tolarjev v pismu in se ukinila. Če bo padlo manj kot 6, bodo izžrebanemu poslali tisoč SIT in postopek ponavljali toliko časa, dokler ne vržejo 6. Vsako naslednjo rundo pa bodo zajeli 3 krat toliko izžrebancev (torej najprej 1, potem 3, potem 9, potem 27 ...), od katerih bo vsak dobil bodisi 1000, bodisi 1000000 tolarjev. Odvisno le od tega, če je prej padla 6 na kocki.
Dobil sem pismo od Agencije. Kolikšna je verjetnost, da so vrgli 6, preden so me izžrebali in mi pisali?
(Sam da ne bi kakšen liml prjavu, da "tok gnarja noben na da kr tko"!)
Agencija javno objavi, da bo metala kocko. Če jim pade 6, bo izžrebala državljana Slovenije in mu poslala milijon tolarjev v pismu in se ukinila. Če bo padlo manj kot 6, bodo izžrebanemu poslali tisoč SIT in postopek ponavljali toliko časa, dokler ne vržejo 6. Vsako naslednjo rundo pa bodo zajeli 3 krat toliko izžrebancev (torej najprej 1, potem 3, potem 9, potem 27 ...), od katerih bo vsak dobil bodisi 1000, bodisi 1000000 tolarjev. Odvisno le od tega, če je prej padla 6 na kocki.
Dobil sem pismo od Agencije. Kolikšna je verjetnost, da so vrgli 6, preden so me izžrebali in mi pisali?
(Sam da ne bi kakšen liml prjavu, da "tok gnarja noben na da kr tko"!)
Man muss immer generalisieren - Carl Jacobi
gzibret ::
> Dobil sem pismo od Agencije. Kolikšna je verjetnost, da so vrgli 6, preden so me izžrebali in mi pisali?
Kar tako na pamet, 0. A ni bilo rečeno, da ko vržejo 6, se ukinejo? Torej se še niso ukinili... Verjetnost, da si v pismu dobil milijon SIT pa je 1/6.
Kar tako na pamet, 0. A ni bilo rečeno, da ko vržejo 6, se ukinejo? Torej se še niso ukinili... Verjetnost, da si v pismu dobil milijon SIT pa je 1/6.
Vse je za neki dobr!
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | nacionalno preverjanje znanja, 9. razred...Oddelek: Šola | 6502 (5947) | onitam |
| » | Dejstvo ali možnost? (strani: 1 2 3 4 5 )Oddelek: Znanost in tehnologija | 26439 (22565) | Saladin |
| » | Najmanjša mera informacijeOddelek: Znanost in tehnologija | 3892 (2337) | Yggdrasil |
| » | Hobotnica Paul (strani: 1 2 )Oddelek: Loža | 11589 (8244) | Nagi Bator |
| » | verjetnostOddelek: Loža | 1862 (1601) | snow |