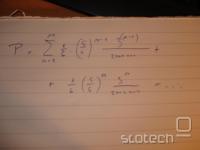Forum » Znanost in tehnologija » Verjetnostne uganke
Verjetnostne uganke
Thomas ::
gzibret:
> Če jim pade 6, bo izžrebala državljana Slovenije in mu poslala milijon tolarjev v pismu in se ukinila.
> Če jim pade 6, bo izžrebala državljana Slovenije in mu poslala milijon tolarjev v pismu in se ukinila.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
> Verjetnost, da si v pismu dobil milijon SIT pa je 1/6.
To, da je večina naslovnikov prejela MILIOJON tolarjev, le manjšina pa TISOČ, te ne moti?
To, da je večina naslovnikov prejela MILIOJON tolarjev, le manjšina pa TISOČ, te ne moti?
Man muss immer generalisieren - Carl Jacobi
Thomas ::
> dej povej, kaj mam narobe...
Še ne, še ne. Daleč prezgodaj!
Še ne, še ne. Daleč prezgodaj!
Man muss immer generalisieren - Carl Jacobi
Fizikalko ::
Hmmm... A pa je orenk narobe, al je samo kakšna malenkost... Lahk tud na ZS, če nočeš teme pokvarit.
Thomas ::
Pejmo počasi! Kaj bi se bilo lahko zgodilo do semle?
Lahko bi padla 6 in sem bi bil izžreban za prvega nagrajenca. Verjetnost za to je 1:12000000. Lahko ne bi padla 6 in in sem bi bil izžreban za prvega nagrajenca. Verjetnost za kaj takega je še 5 krat večja.
Laho sem izpadel v prvem in prišel v drugo kolo. Itd ...
Samo ...
Lahko bi padla 6 in sem bi bil izžreban za prvega nagrajenca. Verjetnost za to je 1:12000000. Lahko ne bi padla 6 in in sem bi bil izžreban za prvega nagrajenca. Verjetnost za kaj takega je še 5 krat večja.
Laho sem izpadel v prvem in prišel v drugo kolo. Itd ...
Samo ...
Man muss immer generalisieren - Carl Jacobi
Fizikalko ::
Ja, sej ni važno , a sem zadel 1000 ali 1000000. Važno je le, da sem izžreban in mi pišejo. To pa je v n-tem žrebanju enako 3^(n-1)/2000000. A ne?
Hkrati mora še veljta, da do takrat ni padla 6: torej (5/6)^n
Pa še seštet je treba po vseh žrebanjih.
Hkrati mora še veljta, da do takrat ni padla 6: torej (5/6)^n
Pa še seštet je treba po vseh žrebanjih.
Fizikalko ::
Čakej, čakej, šele prejle si rekel, da če je nekdo izžreban, izpade...
Jaz nisem tega upošteval - pri mojem izraćunu je št. potencialnih izžrebancev vedno 2 milijona.
Jaz nisem tega upošteval - pri mojem izraćunu je št. potencialnih izžrebancev vedno 2 milijona.
Thomas ::
Dve informaciji imaš. Da imaš več kot 50% pošte zunaj z milijonom tolarjev. Da se ti splača te kuverte vse odkupit po pol milijona SIT.
Pa to, da kocka pade na 6 z verjetnostjo 1/6.
Ti dve na videz nasprotujoči dejstvi moraš spraviti med sabo na način Thomasa Bayesa.
Pa to, da kocka pade na 6 z verjetnostjo 1/6.
Ti dve na videz nasprotujoči dejstvi moraš spraviti med sabo na način Thomasa Bayesa.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Kdo je rekel, da izpadaš? Jaz ne.
Tvoje pismo, ki je eno, pravi, da je to slučajno mogoče, ker pač nimaš dveh.
Tvoje pismo, ki je eno, pravi, da je to slučajno mogoče, ker pač nimaš dveh.
Man muss immer generalisieren - Carl Jacobi
Fizikalko ::
Sicer pa ne vidim nasprotja. Gre za pogojno verjetnost. Vsako žrebanje izračunaš verjetnost, da si izžreban in to pi pogoju, da do tega žrebanja sploh pride. Kaj je s tem narobe? Ta odgovor si mi "dolžan"...
Thomas ::
Ne bom ti zameril, če izračunaš na oba načina. Da si lahko izžreban večkrat, pa da ne moreš biti.
Lahko da boš v stotem kolu prejel za celo Vesolje pošte, prej pa že tudi kar precej (ali nič). Samo ne boš vedel, katero kolo je točno, samo pripisoval verjetnost vsakemu.
Nič ne veš drugega, kot kar sem napisal v kurzivi.
Lahko da boš v stotem kolu prejel za celo Vesolje pošte, prej pa že tudi kar precej (ali nič). Samo ne boš vedel, katero kolo je točno, samo pripisoval verjetnost vsakemu.
Nič ne veš drugega, kot kar sem napisal v kurzivi.
Man muss immer generalisieren - Carl Jacobi
Fizikalko ::
Ah, zdej šele vidim, da sem narobe prebral...
Jaz sem računal, kolikšna je verjetnost, da bodo prej žrebali mene ko vrgli šestico. Nisem prebral, da sem pravkar prejel pismo. Butelj.
OK, bom zračunal zdej kot je treba...
Jaz sem računal, kolikšna je verjetnost, da bodo prej žrebali mene ko vrgli šestico. Nisem prebral, da sem pravkar prejel pismo. Butelj.
OK, bom zračunal zdej kot je treba...
Zgodovina sprememb…
- spremenilo: Fizikalko ()
Fizikalko ::
Hmmm... kolikor gledamm, mislim, da moji prejšnji rešitvi manjka le še množenje z 1/6, pa še (5/6) je ^(n-1) in ne ^n....
Zgodovina sprememb…
- spremenilo: Fizikalko ()
OwcA ::
Občutek imam, da število prebivalcev ne upliva na rešitev, ali bolje rečeno, da mora veljati:
P(1.000) + P(1.000.000) = 1
P(1.000) + P(1.000.000) = 1
Otroška radovednost - gonilo napredka.
Thomas ::
Apriorna verjetnost za 6 je 1/6 - če seveda nobene dodatne informacije ni. Recimo te, da je padlo sodo število.
Dejstvo, da si dobil pismo, pomenilo informacijo, ki je v tem dopolnjenem kontekstu postavila verjetnost na okoli 2/3. Namreč veš, da je 2/3 pisem vsebujočih milijon.
Verjetnost je vedno odvisna od informacije. Verjetnost je glede na informacijo in samo glede na informacijo.
Verjetnost je funkcija informacije.
Dejstvo, da si dobil pismo, pomenilo informacijo, ki je v tem dopolnjenem kontekstu postavila verjetnost na okoli 2/3. Namreč veš, da je 2/3 pisem vsebujočih milijon.
Verjetnost je vedno odvisna od informacije. Verjetnost je glede na informacijo in samo glede na informacijo.
Verjetnost je funkcija informacije.
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Če je verjetnost 100%, je vsa možnost, da se bo zgodilo in nič možnosti da se ne bo.
Man muss immer generalisieren - Carl Jacobi
jvolk ::
Ja in zato pravim 1 proti 1 predstavlja 100%. Zdej kako si ti prestavljaš 1 proti 0.. jaz si ne. Tega si res ne znam razložit.
Recimo če vzameš kocko (6 možnosti) in gledaš kdaj bo padla šestka je pri vsakem metu verjetnost 1 proti 6, da pade šestka (če imaš pošteno kocko ). Recimo da kocko mečeš 10x in da se je 3x zgodilo, da ti je padla šestka. To se pravi 3 proti 10 (od desetih metov so trije zadostovali pogoju)
). Recimo da kocko mečeš 10x in da se je 3x zgodilo, da ti je padla šestka. To se pravi 3 proti 10 (od desetih metov so trije zadostovali pogoju)
Kaj pa tvoj "1 proti 0" (od nič metov je en zadostoval pogoju)?
Got it?
Recimo če vzameš kocko (6 možnosti) in gledaš kdaj bo padla šestka je pri vsakem metu verjetnost 1 proti 6, da pade šestka (če imaš pošteno kocko
Kaj pa tvoj "1 proti 0" (od nič metov je en zadostoval pogoju)?
Got it?
Zgodovina sprememb…
- spremenil: jvolk ()
jeti51 ::
Recimo če vzameš kocko (6 možnosti) in gledaš kdaj bo padla šestka je pri vsakem metu verjetnost 1 proti 6
Verjetnost ni "ena proti šest" ampak "ena šestina". Ustrezno stavno razmerje bi pa bilo "ena proti pet" oziroma v praksi, kjer se daje prednost negativnemu rezultatu, bi se reklo "pet proti ena". Got it?
Imperfect ::
V katerem krogu pa se Thomasova igra najverjetneje zaključi in ali to kaj vpliva na to kakšna je verjetnost za šestico, pa je moje vprašanje.
Pomojem bi se zadeva lepše videla v primeru ko število miljonskih zadetkov proti vsem ne bi tako hitro kovergiralo k 2/3, ali pa bi imeli namesto kocke kovanec (oz. neko stvar z manj kot šestimi izidi).
Pomojem bi se zadeva lepše videla v primeru ko število miljonskih zadetkov proti vsem ne bi tako hitro kovergiralo k 2/3, ali pa bi imeli namesto kocke kovanec (oz. neko stvar z manj kot šestimi izidi).
Thomas ::
V originalu je problem zastavljen celo z dvema metoma kock (in streljanjem izžrebancev, če ne padeta 2 šestici).
Verjetnost je kontraintuitivna. Za nadaljne poglabljanje link!
Verjetnost je kontraintuitivna. Za nadaljne poglabljanje link!
Man muss immer generalisieren - Carl Jacobi
SavoKovac ::
Večina razmišljanj je približnih.
V večini primerov je korektno govoriti o pričakovani verjetnosti za nek dogodek in ne o verjetnosti.
To zato, ker se operira v reduciranem obsegu upoštevanih okoliščin. Ne upošteva se možnih nepričakovanih dogodkov.
Na primer, če vržemo pošteno 6-strano kocko, je verjetnost, da pade 6 pik enaka (1-x)*1/6, kjer je x faktor neupoštevanih okoliščin in v determinističnem sistemu pripada [0,1], v nedeterminističnem pa (0,1).
V večini primerov je korektno govoriti o pričakovani verjetnosti za nek dogodek in ne o verjetnosti.
To zato, ker se operira v reduciranem obsegu upoštevanih okoliščin. Ne upošteva se možnih nepričakovanih dogodkov.
Na primer, če vržemo pošteno 6-strano kocko, je verjetnost, da pade 6 pik enaka (1-x)*1/6, kjer je x faktor neupoštevanih okoliščin in v determinističnem sistemu pripada [0,1], v nedeterminističnem pa (0,1).
Zgodovina sprememb…
- spremenil: SavoKovac ()
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | nacionalno preverjanje znanja, 9. razred...Oddelek: Šola | 6474 (5919) | onitam |
| » | Dejstvo ali možnost? (strani: 1 2 3 4 5 )Oddelek: Znanost in tehnologija | 26403 (22529) | Saladin |
| » | Najmanjša mera informacijeOddelek: Znanost in tehnologija | 3891 (2336) | Yggdrasil |
| » | Hobotnica Paul (strani: 1 2 )Oddelek: Loža | 11572 (8227) | Nagi Bator |
| » | verjetnostOddelek: Loža | 1862 (1601) | snow |