Forum » Znanost in tehnologija » algoritem za tale problem?
algoritem za tale problem?
Sci-Fi ::
En zanimiv problem, ki nam ga je postavu prfoks pri ars1 na fri.
V nekem samostanu z zelo strogo ureditvijo, so stanovali menihi. Vsak je imel svojo sobo v kateri se je posvečal svoji duhovnosti. Enkrat na dan so menihi prišli v skupen prostor na sredo samostana, kjer so obedovali. To je bil njihov edini enkrat dnevni stik.
Zaradi strogega režima, niso smeli duhovniki nikakor komunicirati (na čisto noben način, nobenih namigovanj, tajnih sporočil ipd.). Po obedu se menihi vrnejo nazaj v svoje prostore.
Nekega dne predstojnik samostana pri obedu pove, da se je v samostanu pojavila bolezen, ki jo prepoznaš po tem, da imaš sredi čela eno piko. Okuženih je več kot en in manj kot vseh menihov.
Okuženi morajo zapustiti samostan.
Klub ničelni komunikaciji so naslednji dan res vsi okuženi menihi zapustili samostan.
To pomeni, da jih zjutraj ni bilo več.
Pa v sobah niso imeli ogledal.
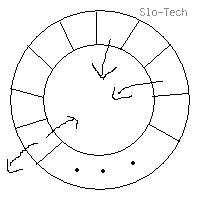
Samostan izgleda takole:
Naloga je sestaviti algoritem po katerem so ugotovili, da so okuženi in so odšli.
Prof. nam je namignil da matematična indukcija ni dovolj.
Že za tri je problem sila težak.
Kaj pa vi pravite?
Jst verjetno zvem rešitev ta četrtek.
V nekem samostanu z zelo strogo ureditvijo, so stanovali menihi. Vsak je imel svojo sobo v kateri se je posvečal svoji duhovnosti. Enkrat na dan so menihi prišli v skupen prostor na sredo samostana, kjer so obedovali. To je bil njihov edini enkrat dnevni stik.
Zaradi strogega režima, niso smeli duhovniki nikakor komunicirati (na čisto noben način, nobenih namigovanj, tajnih sporočil ipd.). Po obedu se menihi vrnejo nazaj v svoje prostore.
Nekega dne predstojnik samostana pri obedu pove, da se je v samostanu pojavila bolezen, ki jo prepoznaš po tem, da imaš sredi čela eno piko. Okuženih je več kot en in manj kot vseh menihov.
Okuženi morajo zapustiti samostan.
Klub ničelni komunikaciji so naslednji dan res vsi okuženi menihi zapustili samostan.
To pomeni, da jih zjutraj ni bilo več.
Pa v sobah niso imeli ogledal.
Samostan izgleda takole:
Naloga je sestaviti algoritem po katerem so ugotovili, da so okuženi in so odšli.
Prof. nam je namignil da matematična indukcija ni dovolj.
Že za tri je problem sila težak.
Kaj pa vi pravite?
Jst verjetno zvem rešitev ta četrtek.
Sci-Fi is the best way to dream
- zavaroval slike: Predator ()
Thomas ::
Če vidiš samo enega s piko, jo imaš ti tudi. Zapustiš samostan. Tako bo naredil tudi drugi s piko...
Man muss immer generalisieren - Carl Jacobi
Sci-Fi ::
rad bi imel algoritem za n
Ta algoritem deluje če imata dva piko, in veš da sta dva, kaj pa če ne veš da sta dva?
Če veš da ima piko samo eden je u izi.
Ta algoritem deluje če imata dva piko, in veš da sta dva, kaj pa če ne veš da sta dva?
Če veš da ima piko samo eden je u izi.
Sci-Fi is the best way to dream
Zgodovina sprememb…
- spremenil: Sci-Fi ()
b4d ::
No idea, morda pa so se slabo počutli, ker so bli bolani pa so šli  joke, dej res rešitev tle napopej, ki me prou zanima.
joke, dej res rešitev tle napopej, ki me prou zanima.
b4d.sablun.org
Thomas ::
Naloga je tukaj rahlo slabo zastavljena. Drugo jutro imamo rešitev le v primeru, da je minimalno dovoljeno število okuženih. Sicer je treba dopustiti več dni.
Man muss immer generalisieren - Carl Jacobi
kyon ::
1. Ni prfoks za ars1, ampak APS1.
2. Takole se pa resi ta problem:
Imas recimo 10 menihov. 4 okuzeni, 6 ne.
Kaj naredit, ce si eden od menihov? Pogledas koliko menihov(razen sebe) ima piko. Ce si okuzen vidis 3 pike, ce nisi vidis 4 pike. Ok? Vsak menih(ker so seveda intelektulci vsi to pogruntajo) rece: Po k dnevih bom zapustil samostan, kjer je k stevilo pik, ki jih je videl. Tisti, ki so videli 3 pike(okuzeni torej) bodo samostan zapustili dan pred neokuzenimi. In glej no glej, po 3 dnevih ostanejo samo se neokuzeni menihi. Ti seveda vedo, da to pomeni, da niso okuzeni.
Problem resen. Ups, zdaj vidim, odsli so ze naslednji dan. Moja resitev deluje, samo za vec dni. Si siguren, da je rekel, da ze naslednji dan okuzenih ni vec?
LP
kyon
2. Takole se pa resi ta problem:
Imas recimo 10 menihov. 4 okuzeni, 6 ne.
Kaj naredit, ce si eden od menihov? Pogledas koliko menihov(razen sebe) ima piko. Ce si okuzen vidis 3 pike, ce nisi vidis 4 pike. Ok? Vsak menih(ker so seveda intelektulci vsi to pogruntajo) rece: Po k dnevih bom zapustil samostan, kjer je k stevilo pik, ki jih je videl. Tisti, ki so videli 3 pike(okuzeni torej) bodo samostan zapustili dan pred neokuzenimi. In glej no glej, po 3 dnevih ostanejo samo se neokuzeni menihi. Ti seveda vedo, da to pomeni, da niso okuzeni.
Problem resen. Ups, zdaj vidim, odsli so ze naslednji dan. Moja resitev deluje, samo za vec dni. Si siguren, da je rekel, da ze naslednji dan okuzenih ni vec?
LP
kyon
Zgodovina sprememb…
- spremenil: kyon ()
Brane2 ::
?e vidi? samo enega s piko, jo ima? ti tudi. Zapusti? samostan. Tako bo naredil tudi drugi s piko...
To velja samo, ce sta okuzena dva. Od tam naprej je easy. Kaj pa ce so trije ali vec ?
Bojim se, da se bo v koncni resitvi, da so duhovniki vendarle nekako komunicirali med sabo, ceprav posredno....
Brane2 ::
kyon:
ampak tvoja resitev zahteva poprejsen dogovor menihov.
O.K., recimo da vzames kot casovno enoto vsak nalsednji shod ob vecerji. Ker pa toliko casa ni vec na razpolago, se je treba za vse ostale enote zmenit.
Poleg tega bi morala biti ta resitev edina mozna, da torej odpadejo dogovori okrog uporabljene resitve...
ampak tvoja resitev zahteva poprejsen dogovor menihov.
O.K., recimo da vzames kot casovno enoto vsak nalsednji shod ob vecerji. Ker pa toliko casa ni vec na razpolago, se je treba za vse ostale enote zmenit.
Poleg tega bi morala biti ta resitev edina mozna, da torej odpadejo dogovori okrog uporabljene resitve...
bili_39 ::
Če so pri obedu imajo verjetno kake žlice - ogledala. Rečeno je bilo, da v sobah nimajo ogledal - ne pa v skupnem prostoru.
Thomas ::
Brane - pojdi še enkrat skozi in skozi link, ki sem ga dal. Stvar je kristalno jasna. VEČ DNI rabijo.
Man muss immer generalisieren - Carl Jacobi
Sci-Fi ::
Res je predmet je aps1 ne ars:
Ampak pol nam je prfoks narobe zastavu nalogo.
Rekel je naslednji dan in v enem izmed naslednjih dni.
Pri drugače zastavljeni nalogi pa je algoritem kul.
bili_39
Take stvari odpadejo. Smo profa posebej vprašali.
Ampak pol nam je prfoks narobe zastavu nalogo.
Rekel je naslednji dan in v enem izmed naslednjih dni.
Pri drugače zastavljeni nalogi pa je algoritem kul.
bili_39
Take stvari odpadejo. Smo profa posebej vprašali.
Sci-Fi is the best way to dream
DMouse ::
Ali po domače rečeno - I was right all along!
Tvoj prvi odgovor me ni čisto prepričal
Sicer pa link vse pove... nisem si mislil da je rešitev tako enostavna
Tvoj prvi odgovor me ni čisto prepričal
Sicer pa link vse pove... nisem si mislil da je rešitev tako enostavna
Thomas ::
Dobiš e-mail:
Spoštovani! Obveščamo vas, da boste dobili milijon dolarjev, če jutri med 11:00 in 12:00 EDINI pokličete na 555-1234567. Še 5 ljudi je dobilo e-mail s prav tako vsebino. Če jih boste iskali, vas bomo diskvalificirali, sicer se pa lahko še večkrat nadejate take pošte. Lp, Illuminati.
Kaj naj storiti, če veš da je zadeva resnična in noben hoax?
Spoštovani! Obveščamo vas, da boste dobili milijon dolarjev, če jutri med 11:00 in 12:00 EDINI pokličete na 555-1234567. Še 5 ljudi je dobilo e-mail s prav tako vsebino. Če jih boste iskali, vas bomo diskvalificirali, sicer se pa lahko še večkrat nadejate take pošte. Lp, Illuminati.
Kaj naj storiti, če veš da je zadeva resnična in noben hoax?
Man muss immer generalisieren - Carl Jacobi
Brane2 ::
Sem sel skozi link.
In opazil nekaj razlik. Prva je ta, da je tam podano, da je samostan "ociscen" po treh vecerjah, tu pa takoj naslednje jutro, druga pa ta, da je tam podano, da je bolan vsaj en duhovnik, tu pa vsaj dva.
Aja, poleg tega tu udelezencem ni dano posiljanje informacije skozi samomor.
Edina resitev, ki jo vidim, je da najdejo nek arbitracijski protokol, ki je obenem edini mozen, tako da se ni treba o njem posebej pogajati.
In tretjic, dogovorjen je nacin razmisljanja. Vsak duhovnik se torej mora vprasati prvi vecer, ali sploh vidi koga s piko itd.
Kaj pa, ce prvi vecer opazijo vsi, da imata dva/trije duhovniki piko ? Torej okuzeni duhovniki vidijo dve piki in ne morejo vedeti, ali imajo na svojem celu tretjo, neokuzeni pa vidijo 3 in razmislajo o cetrti.
Stvar dela samo, ce duhovnik zapre oci na vsaki vecerji do spanja, ko vidi novo piko...
Naloga OP je bila zastavljena precej drugace...
In opazil nekaj razlik. Prva je ta, da je tam podano, da je samostan "ociscen" po treh vecerjah, tu pa takoj naslednje jutro, druga pa ta, da je tam podano, da je bolan vsaj en duhovnik, tu pa vsaj dva.
Aja, poleg tega tu udelezencem ni dano posiljanje informacije skozi samomor.
Edina resitev, ki jo vidim, je da najdejo nek arbitracijski protokol, ki je obenem edini mozen, tako da se ni treba o njem posebej pogajati.
In tretjic, dogovorjen je nacin razmisljanja. Vsak duhovnik se torej mora vprasati prvi vecer, ali sploh vidi koga s piko itd.
Kaj pa, ce prvi vecer opazijo vsi, da imata dva/trije duhovniki piko ? Torej okuzeni duhovniki vidijo dve piki in ne morejo vedeti, ali imajo na svojem celu tretjo, neokuzeni pa vidijo 3 in razmislajo o cetrti.
Stvar dela samo, ce duhovnik zapre oci na vsaki vecerji do spanja, ko vidi novo piko...
Naloga OP je bila zastavljena precej drugace...
Zgodovina sprememb…
- spremenil: Brane2 ()
Thomas ::
Ne, ne - link je povsem korekten. Tukaj zastavljena naloga pa ima lahko SAMO MOJO rešitev. Think harder! 
Man muss immer generalisieren - Carl Jacobi
McHusch ::
Thomas. Izbereš šest kuglic in jih oštevilčiš od 1 do 6. Izžrebaš eno in če ima številko 1, pošlješ. [In upaš, da so vsi storili enako.] ;)
DMouse ::
Thomas: Ja sedaj sem opazil da piše "okužen več kot en", jaz sem razmišljal za primer "okužen je vsaj en". Pa še v tem primeru je tvoj odgovor samo polovičen (res pa je da je boljši od vseh drugih možnih  )
)
Brane2 ::
O.K. Recimo da je pet duhovnikov z belo piko na celu in da se lahko hecajo vec dni.
Kako bi sla resitev ?
Za 1,2,3 mi je jasno. Kako gre, ce jih je pet ?
S tem, da je tudi to sleparjenje, ker vsak duhovnik s svojim (ne)odhodom poslje svoj bit informacije ostalim, a naj bo...
Kako bi sla resitev ?
Za 1,2,3 mi je jasno. Kako gre, ce jih je pet ?
S tem, da je tudi to sleparjenje, ker vsak duhovnik s svojim (ne)odhodom poslje svoj bit informacije ostalim, a naj bo...
DMouse ::
Če je vsaj eden (in ne vsi) okužen ter imajo na voljo dovolj dni, je problem očitno rešljiv. Prvi dan pogledaš koliko menihov ima piko (recimo k), počakaš k noči, če v k-ti noči vsi s piko ne odidejo, moraš naslednjo noč oditi ti (skupaj z ostalimi).
bili_39 ::
Mislim, da je kyonova rešitev pravilna za ta problem. Thomasov link ima druge pogoje.
Kaj naredit, ce si eden od menihov? Pogledas koliko menihov(razen sebe) ima piko. Ce si okuzen vidis 3 pike, ce nisi vidis 4 pike. Ok? Vsak menih(ker so seveda intelektulci vsi to pogruntajo) rece: Po k dnevih bom zapustil samostan, kjer je k stevilo pik, ki jih je videl. Tisti, ki so videli 3 pike(okuzeni torej) bodo samostan zapustili dan pred neokuzenimi. In glej no glej, po 3 dnevih ostanejo samo se neokuzeni menihi. Ti seveda vedo, da to pomeni, da niso okuzeni.
Lahko odidejo že naslednji dan, saj lahko 3 odštejejo od k in prvi možni odhod bi bil takoj. Tisti, ki vidi 3 pike lahko predvideva, da je okuženih najmanj 3 in največ 4 (predvidevati mora, da jih je 3 in da dva vidita samo 2 piki. Tisti, ki jih vidijo 4 vedo: najmanj 4 in največ 5. , vendar morajo predvidevati, da jih drugi vidijo eno manj - 3 In to vedo vsi, saj so logiki. Torej vsi vedo, da jih je najmanj 2 in največ 5 - vsak od števila pik, ki jih vidi odšteje 2 in odide po k-2 dneh...
Kaj naredit, ce si eden od menihov? Pogledas koliko menihov(razen sebe) ima piko. Ce si okuzen vidis 3 pike, ce nisi vidis 4 pike. Ok? Vsak menih(ker so seveda intelektulci vsi to pogruntajo) rece: Po k dnevih bom zapustil samostan, kjer je k stevilo pik, ki jih je videl. Tisti, ki so videli 3 pike(okuzeni torej) bodo samostan zapustili dan pred neokuzenimi. In glej no glej, po 3 dnevih ostanejo samo se neokuzeni menihi. Ti seveda vedo, da to pomeni, da niso okuzeni.
Lahko odidejo že naslednji dan, saj lahko 3 odštejejo od k in prvi možni odhod bi bil takoj. Tisti, ki vidi 3 pike lahko predvideva, da je okuženih najmanj 3 in največ 4 (predvidevati mora, da jih je 3 in da dva vidita samo 2 piki. Tisti, ki jih vidijo 4 vedo: najmanj 4 in največ 5. , vendar morajo predvidevati, da jih drugi vidijo eno manj - 3 In to vedo vsi, saj so logiki. Torej vsi vedo, da jih je najmanj 2 in največ 5 - vsak od števila pik, ki jih vidi odšteje 2 in odide po k-2 dneh...
Thomas ::
McHusch, you are correct.
Man muss immer generalisieren - Carl Jacobi
Zgodovina sprememb…
- spremenil: Thomas ()
Sci-Fi ::
Ok sem še enkrat pogledu u zapiske pa je tam res vsaj eden in ne več kot eden.
Sam za dneve sem pa ziher da je reku naslednji dan in ne v naslednjih dneh.
Tko da se je verjetno res v tem zmotu.
tist z miljoni je pa zgolj kockanje
:)
Sam za dneve sem pa ziher da je reku naslednji dan in ne v naslednjih dneh.
Tko da se je verjetno res v tem zmotu.
tist z miljoni je pa zgolj kockanje
:)
Sci-Fi is the best way to dream
Thomas ::
Ne ni "le kockanje". Tako si maksimiziraš verjetnost, da boš kaj dobil.
Man muss immer generalisieren - Carl Jacobi
DMouse ::
Thomas: vsak naključen algoritem, ki ti v šestini primerov vrne "true", je ok. Vendar pa (tudi če vsi storijo enako) ne zagotavlja nagrade 
Thomas ::
Zagotavlja ti je ne. Ampak če se odločiš za algoritem ki ima manjšo ali večjo vrednost od 1/6, si možnosti še zmanjšaš. Pa kaj grdo gledaš?
Man muss immer generalisieren - Carl Jacobi
Sci-Fi ::
Važno je da šanse so. Sej če pol nekajkrat dobiš tak mejl je pa že verjetnost, da ne zadaneš dost vlka.
Ko bi vsaj kdo res kr tko talal dnar.
:)
Ko bi vsaj kdo res kr tko talal dnar.
:)
Sci-Fi is the best way to dream
DMouse ::
Grdo gledam ker ne maram da verjetnost odloča o tem ali bom dobil nagrado 
Zgodovina sprememb…
- spremenil: DMouse ()
Thomas ::
No, jest sem ga že. 1000 pokojnih DEM bi dobil, kdor bi se edini oglasil s tega foruma do nekega datuma.
Man muss immer generalisieren - Carl Jacobi
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | pomoč matematika - kombinatorika!Oddelek: Šola | 1513 (1177) | technolog |
| » | DalajlamaOddelek: Loža | 3082 (2386) | Thomas |
| » | Župnik za spolne napade dobil pogojno kazen (strani: 1 2 )Oddelek: Loža | 22984 (21370) | atubbuta |
| » | Krutost ki se dogaja v TibetuOddelek: Problemi človeštva | 2796 (2203) | drejc |
| » | [Potopis]: MoskvaOddelek: Loža | 3552 (2955) | TeraSonic++ |