Forum » Šola » Statistika
Statistika
GangStarr ::
Pozdravljeni!
Imam nekaj vprašanj, ki se nanašajo na statistiko, zato vas prosim za pomoč.
Imamo na primer naslednje podatke:
503, 1102, 2067, 1108, 1505, 799, 1498, 1612, 511, 832, 2089, 1614, 791, 1992, 834, 1635, 1182, 865.
1. Kako lahko te podatke uredim v razrede (npr. v štiri)? Kakšen postopek je tu?
2. Kako lahko iz danih podatkov izračunam frekvenčno porazdelitev?
3. Še vprašanje o histogramih. Kdaj uporabim takšen histogram 1. in kdaj takšnega 2.? Razlika je v x osi. Enkrat označimo sredino razreda (2.), enkrat pa zgornjo in spodnjo mejo razreda oz. kako se temu reče (1.).
Imam nekaj vprašanj, ki se nanašajo na statistiko, zato vas prosim za pomoč.
Imamo na primer naslednje podatke:
503, 1102, 2067, 1108, 1505, 799, 1498, 1612, 511, 832, 2089, 1614, 791, 1992, 834, 1635, 1182, 865.
1. Kako lahko te podatke uredim v razrede (npr. v štiri)? Kakšen postopek je tu?
2. Kako lahko iz danih podatkov izračunam frekvenčno porazdelitev?
3. Še vprašanje o histogramih. Kdaj uporabim takšen histogram 1. in kdaj takšnega 2.? Razlika je v x osi. Enkrat označimo sredino razreda (2.), enkrat pa zgornjo in spodnjo mejo razreda oz. kako se temu reče (1.).
Semper Fi
otago ::
V pomoc:
http://studentski.net/gradivo/ulj_fup_u...
Prirocnik: (prvih 8 strani)
http://studentski.net/gradivo/ulj_fri_r...
http://studentski.net/gradivo/ulj_fup_u...
Prirocnik: (prvih 8 strani)
http://studentski.net/gradivo/ulj_fri_r...
Zgodovina sprememb…
- spremenilo: otago ()
Blop ::
formule, ki jih rabiš:
število razredov dobiš tkole: K=1+log2N oz. N=1+3.322logN (torej, glede na tvoje podatke imaš 5 razredov)
izračun enkih širin razredov: ik=d= (ymax-Ymin)/K
značilne vrednosti k:
- spodnja meja: Yk,s
- zgornja meja: Yk,z = yk+1s
- širina ik:=yk,z-yk,s
- sredina razreda yk= (yk,s + yk,z)/2
Frekvanca razreda fk (prešteješ števila v posameznem razredu)
Relativna frekenca f* =fk/N
Komulativa frekvenc razreda Fk=Fk-1+fk
p.s. poglej si še kje kak primer, ker imam občutek, da pojma nimaš, kaj ti pove frekvenca, MO, Me, itd. v praksi.
Histograma sta pa oba ista, le da je pri enem poimenovana neodvisna spremenljivka X.
število razredov dobiš tkole: K=1+log2N oz. N=1+3.322logN (torej, glede na tvoje podatke imaš 5 razredov)
izračun enkih širin razredov: ik=d= (ymax-Ymin)/K
značilne vrednosti k:
- spodnja meja: Yk,s
- zgornja meja: Yk,z = yk+1s
- širina ik:=yk,z-yk,s
- sredina razreda yk= (yk,s + yk,z)/2
Frekvanca razreda fk (prešteješ števila v posameznem razredu)
Relativna frekenca f* =fk/N
Komulativa frekvenc razreda Fk=Fk-1+fk
p.s. poglej si še kje kak primer, ker imam občutek, da pojma nimaš, kaj ti pove frekvenca, MO, Me, itd. v praksi.
Histograma sta pa oba ista, le da je pri enem poimenovana neodvisna spremenljivka X.
komentar2021 ::
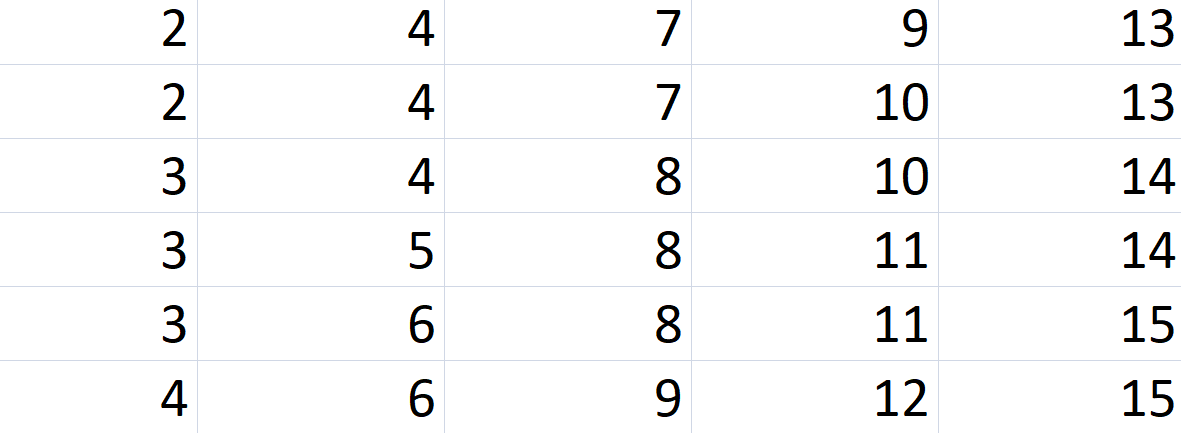
Bom si izposodil to temo: V nekem kraju so želeli ugotoviti, kako se porazdeljuje število udeležencev manjših prireditev, ki jih organizirajo v čast obletnice nekega skladatelja. Prikazani so podatki o številu udeležencev za posamezno prireditev: 15, 8, 9, 10, 11, 6, 4, 14, 15, 4, 6, 13, 14, 7, 8, 15, 11, 12, 7, 8, 9, 10, 13, 15, 15
1. Podatke razvrstite v frekvenčno porazdelitev po modelu nezvezne spremenljivke po Sturgesovem pravilu.
2. Prikažite prave spodnje in zgornje meje razredov, da zagotovite kontinuiranost.
3. Izračunajte kumulativo ,,nad"
Kar se tiče prve naloge: Sturgesovo pravilo: 1+3.3*log(kumulativna frekvenca). Predvidevam, da pač preštejemo vse te številke (število udeležencev) in dobimo 1+3.3*log25 = 5.61 (torej 6 razredov, ker zaključujemo navzgor. Zanima me samo, kako bi hitreje dobil to število pri logaritmiranju, torej v tem primeru 25, ker se mi zdi nenavadano, da bi vse prešteval, lahko bi bilo tudi nekaj sto podatkov? Sem pregledal zgornje poste in linke.
1. Podatke razvrstite v frekvenčno porazdelitev po modelu nezvezne spremenljivke po Sturgesovem pravilu.
2. Prikažite prave spodnje in zgornje meje razredov, da zagotovite kontinuiranost.
3. Izračunajte kumulativo ,,nad"
Kar se tiče prve naloge: Sturgesovo pravilo: 1+3.3*log(kumulativna frekvenca). Predvidevam, da pač preštejemo vse te številke (število udeležencev) in dobimo 1+3.3*log25 = 5.61 (torej 6 razredov, ker zaključujemo navzgor. Zanima me samo, kako bi hitreje dobil to število pri logaritmiranju, torej v tem primeru 25, ker se mi zdi nenavadano, da bi vse prešteval, lahko bi bilo tudi nekaj sto podatkov? Sem pregledal zgornje poste in linke.
kljuka13 ::
komentar2021 je izjavil:
Bom si izposodil to temo: V nekem kraju so želeli ugotoviti, kako se porazdeljuje število udeležencev manjših prireditev, ki jih organizirajo v čast obletnice nekega skladatelja. Prikazani so podatki o številu udeležencev za posamezno prireditev: 15, 8, 9, 10, 11, 6, 4, 14, 15, 4, 6, 13, 14, 7, 8, 15, 11, 12, 7, 8, 9, 10, 13, 15, 15
1. Podatke razvrstite v frekvenčno porazdelitev po modelu nezvezne spremenljivke po Sturgesovem pravilu.
2. Prikažite prave spodnje in zgornje meje razredov, da zagotovite kontinuiranost.
3. Izračunajte kumulativo ,,nad"
Kar se tiče prve naloge: Sturgesovo pravilo: 1+3.3*log(kumulativna frekvenca). Predvidevam, da pač preštejemo vse te številke (število udeležencev) in dobimo 1+3.3*log25 = 5.61 (torej 6 razredov, ker zaključujemo navzgor. Zanima me samo, kako bi hitreje dobil to število pri logaritmiranju, torej v tem primeru 25, ker se mi zdi nenavadano, da bi vse prešteval, lahko bi bilo tudi nekaj sto podatkov? Sem pregledal zgornje poste in linke.
Hmm, ne znam si zares predstavljati, kaj bi lahko bilo še hitrejši način kot pa enostavno prešteti število meritev :-) Če bi imel mnogo več meritev, bi jih verjetno imel shranjene v računalniku in ti jih ne bi bilo treba šteti na roko ...
komentar2021 ::
V neki manjši prodajalni idrijskih čipk so želeli ugotoviti, kako se porazdeljuje število prodanih prtičkov po dnevih. Količine so razvrstili od najmanjših do največjih.
a)Podatke razvrstite v frekvenčno porazdelitev po modelu zvezne spremenljivke po Sturgesovem pravilu, ob uporabi besede "pod".
Sturgesovo pravilo: 1+3.3*log(število enot, v našem primeru 30)=5.87
Potem bi izračunal širino razredov, naredil tabelo...
Zanima me, kaj je mišljeno s tem "ob uporabi besede pod"? Kako to vključim pri izračunu?
a)Podatke razvrstite v frekvenčno porazdelitev po modelu zvezne spremenljivke po Sturgesovem pravilu, ob uporabi besede "pod".
Sturgesovo pravilo: 1+3.3*log(število enot, v našem primeru 30)=5.87
Potem bi izračunal širino razredov, naredil tabelo...
Zanima me, kaj je mišljeno s tem "ob uporabi besede pod"? Kako to vključim pri izračunu?
Zgodovina sprememb…
- spremenilo: komentar2021 ()
kljuka13 ::
Pri razvrščanju v frekvenčno porazdelitev je treba biti pozoren, kaj se dogaja na mejah razredov. Edino smiselno je, da je vsaka meritev vključena zgolj in natanko v en razred. Zaradi tega pri določanju mej razredov običajno eno izmed meja postavimo kot "odprto mejo" (ne vključuje meje), drugo kot "zaprto mejo" (vključuje mejo). Primer: naj bo širina razreda 2 in podatki od 2 do 8. Tedaj so razredi: 2-4, 4-6, 6-8. V kateri razred bomo vključili meritev, ki znaša natanko 4? V prvi ali v drugi razred? Lahko se odločimo:
Če naredimo razrede po metodi "pod", potem se bodo razredi imenovali "2 do pod 4", "4 do pod 6" in "6 do pod 8" oziroma z matematičnim zapisom:
Če naredimo razrede po metodi "nad", potem se bodo razredi imenovali "nad 2 do 4", "nad 4 do 6", "nad 6 do 8" oziroma z matematičnim zapisom:
Pri metodi "pod" je torej v razred vključena spodnja meja, pri metodi "nad" pa zgornja meja.
Če naredimo razrede po metodi "pod", potem se bodo razredi imenovali "2 do pod 4", "4 do pod 6" in "6 do pod 8" oziroma z matematičnim zapisom:
2 <= x < 4, 4 <= x < 6 in 6 <= x < 8V tem primeru bo meritev 4 padla v drugi razred. Znak <= pomeni manjše ali enako kot.
Če naredimo razrede po metodi "nad", potem se bodo razredi imenovali "nad 2 do 4", "nad 4 do 6", "nad 6 do 8" oziroma z matematičnim zapisom:
2 < x <= 4, 4 < x <= 6 in 6 < x <= 8V tem primeru bo meritev 4 padla v prvi razred.
Pri metodi "pod" je torej v razred vključena spodnja meja, pri metodi "nad" pa zgornja meja.
Zgodovina sprememb…
- spremenil: kljuka13 ()
komentar2021 ::
Najlepša hvala za odgovor. Zanima me tudi, kakšna je razlika pri računanju kumulative "pod" ali kumulative "nad"? Ugibam, da enostavno izračunamo kumulativno frekvenco?
kljuka13 ::
Tako je, velja isto kot pri frekvenčni porazdelitvi. Razredi so lahko "pod 4", "pod 6", "pod 8" (x < 4, x < 6, x < 8) ali pa "do 4", "do 6", "do 8" (x <= 4, x <= 6, x <= 8).
komentar2021 ::
OK, hvala. Kakšna pa je razlika pri uporabi Sturgesovega pravila, glede na to ali gre za model zvezne ali nezvezne spremenljivke?
komentar2021 ::
V navodilih za to nalogo imamo dvakrat da določamo št. razredov, sredino razredo in širino razredov po Sturgesu, zakaj oz. kako se razlikuje izračun drugega primera glede na prvi, saj so podatki enaki? V čem se razlikuje prvi izračun glede na drugega? Kako prikažemo kumulativo glede na statistično pravilo? Vem, kako se sicer računajo kumulative, tako, da pač seštejemo frekvenco s prejšnjo kumulativo, kumulativo za prvi razred je enaka frekvenci.
Zgodovina sprememb…
- spremenilo: komentar2021 ()
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Statistika 1 izračun kvantilaOddelek: Šola | 1204 (965) | bajsibajsi |
| » | Potrošnja in lenuhi (strani: 1 2 )Oddelek: Problemi človeštva | 10937 (9424) | globalna80 |
| » | StatistikaOddelek: Šola | 2376 (1688) | Hardstyle |
| » | Kaj je res, da ...Oddelek: Mobilne tehnologije | 5244 (4644) | BBB |