Forum » Šola » graf funkcije
graf funkcije

marko181914 ::
Mi lahko nekdo razloži zakaj je graf te funkcije: (x^2-2x)/(x^3-3x+2) na intervalu [0,2] takšen in kako se nariše ta graf ? Hvala za pomoč!
- spremenil: marko181914 ()
Tezaab ::
Padajoc je, ker je v števcu vedno nepozitivna vrednost (na tem intervalu je x^2 vedno manj ali enako 0).
Os X seka v točkah x=0 in x=2 (ničli števca, rešiš enačbo x^2-2x=0). V točki x=1 ima asimptoto, ker te vrednosti ne bo nikoli dosegla (ena od ničel imenovalca, ki je na tem intervalu).
Torej okvirno ga s tem določiš, detajlov risanja grafov se pa ne spomnim več - razen tega, da te brute force metoda, ko vstaviš par točk z intervala v funkcijo in vidiš kaj dobiš ven ter nato potegneš krivuljo lahko pošteno zafrkne.
Os X seka v točkah x=0 in x=2 (ničli števca, rešiš enačbo x^2-2x=0). V točki x=1 ima asimptoto, ker te vrednosti ne bo nikoli dosegla (ena od ničel imenovalca, ki je na tem intervalu).
Torej okvirno ga s tem določiš, detajlov risanja grafov se pa ne spomnim več - razen tega, da te brute force metoda, ko vstaviš par točk z intervala v funkcijo in vidiš kaj dobiš ven ter nato potegneš krivuljo lahko pošteno zafrkne.
sisemen: "Inženirstvo je v nenehni tekmi z vesoljem. Trudi se izdelati
tehnologijo, ki je odporna na idiote, vesolje pa se trudi izdelati vedno
hujše idiote. In vesolje zmaguje."
tehnologijo, ki je odporna na idiote, vesolje pa se trudi izdelati vedno
hujše idiote. In vesolje zmaguje."

Unknown_001 ::
Ničle števca so ničle funkcije. Če gre za soden ničle, graf ne seka x osi, če so ničle lihe in večje od 1, funkcija tvori "sedlo".
Rimske številke kažejo stopnje ničel.
Ničle imenovalca so poli (navpične asimptote). Funkcija se jim približuje a jih ne doseže, ker tam ni definirana zaradi tega ker velja X/0=neskončno. Tu je pravtako važno ali gre za sode ničle ali lihe, ker ti pove, kako se funkcija zvije na vsaki strani polov.
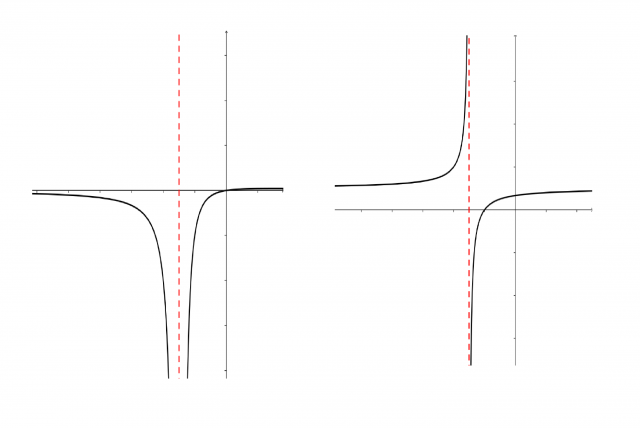
Levo primer sodega pola, desno primer lihega pola.
Vodoravna (k=0) ali poševna asimptota je rezultat deljenja imenovalca z količnikom (pravila za deljenje polinomov) Ostanka ne šteješ
Predznak ti tudi pove kako je funkcija obrnjena.
Rimske številke kažejo stopnje ničel.
Ničle imenovalca so poli (navpične asimptote). Funkcija se jim približuje a jih ne doseže, ker tam ni definirana zaradi tega ker velja X/0=neskončno. Tu je pravtako važno ali gre za sode ničle ali lihe, ker ti pove, kako se funkcija zvije na vsaki strani polov.
Levo primer sodega pola, desno primer lihega pola.
Vodoravna (k=0) ali poševna asimptota je rezultat deljenja imenovalca z količnikom (pravila za deljenje polinomov) Ostanka ne šteješ
Predznak ti tudi pove kako je funkcija obrnjena.
Wie nennt man einen Moderator mit der Hälfte des Gehirnis ?
Begabt
Begabt
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
lebdim ::
Ja, ampak pri racionalnih funkcijah je tako pri poševnih / vodoravnih asimptotah:
- če je stopnja števca > stopnja imenovalca, potem je treba opraviti deljenje in upoštevaš količnik, ki ga pri tem deliš
- če je stopnja števca = stopnja imenovalca, je vodoravna asimptota y = 1
- če je stopnja števca < stopnja imenovalca, je vodoravna asimptota y = 0
V tem primeru velja zadnje, in je zato vodoravna asimptota y = 0. To je tudi limita te funkcije.
- če je stopnja števca > stopnja imenovalca, potem je treba opraviti deljenje in upoštevaš količnik, ki ga pri tem deliš
- če je stopnja števca = stopnja imenovalca, je vodoravna asimptota y = 1
- če je stopnja števca < stopnja imenovalca, je vodoravna asimptota y = 0
V tem primeru velja zadnje, in je zato vodoravna asimptota y = 0. To je tudi limita te funkcije.
Zgodovina sprememb…
- spremenil: lebdim ()

Unknown_001 ::
marko181914 je izjavil:
Mi lahko nekdo razloži zakaj je graf te funkcije: (x^2-2x)/(x^3-3x+2) na intervalu [0,2] takšen in kako se nariše ta graf ? Hvala za pomoč!
Mi je pa rešitev sporna, saj če je x=1 pol funkcije tam funkcija sploh ni definirana in ne vem kako lahko to vključiš v interval... Meni bi bilo bolj logično (0,1)(1,2), če je vodoravna asimptota y=0
Wie nennt man einen Moderator mit der Hälfte des Gehirnis ?
Begabt
Begabt
Zgodovina sprememb…
- spremenilo: Unknown_001 ()
lebdim ::
@RaptorF16,
iz grafa (iz spletne strani wolframalpha) se natančno vidi, da je v x = 1 pol. Ker je graf tam pretrgan. Sicer je pa to zgolj navodilo naloge. In je na strani študenta, da veš, kako se ta zaprti interval [0..2] razdeli (kot si že sam napisal).
iz grafa (iz spletne strani wolframalpha) se natančno vidi, da je v x = 1 pol. Ker je graf tam pretrgan. Sicer je pa to zgolj navodilo naloge. In je na strani študenta, da veš, kako se ta zaprti interval [0..2] razdeli (kot si že sam napisal).
Yacked2 ::
Ja, ampak pri racionalnih funkcijah je tako pri poševnih / vodoravnih asimptotah:
- če je stopnja števca > stopnja imenovalca, potem je treba opraviti deljenje in upoštevaš količnik, ki ga pri tem deliš
- če je stopnja števca = stopnja imenovalca, je vodoravna asimptota y = 1
- če je stopnja števca < stopnja imenovalca, je vodoravna asimptota y = 0
V tem primeru velja zadnje, in je zato vodoravna asimptota y = 0. To je tudi limita te funkcije.
Če je stopnja števca = stopnji imenovalca, je vodoravna asimpotoa a/b, kjer je a vodilni člen števca in b vodilni člen imenovalca!
Korak naprej ni vedno ustrezen...sploh če si na robu prepada!
lebdim ::
@Yacked2,
ja saj res, maš prav, hehehe malo na hitro sem privzel, da sta oba vodilna koeficienta 1.
malo na hitro sem privzel, da sta oba vodilna koeficienta 1.
ja saj res, maš prav, hehehe

marko181914 ::
Če je padajoč ni nujno da je takšen? Torej se je za vsak bolj kompleksen racionalen graf treba j****ti z bisekcijo, ker vem da bi z bisekcijo intervala [0, 1/2], lahko narisal točno takšen graf??
Zgodovina sprememb…
- spremenil: marko181914 ()
lebdim ::
Model, kakšna bisekcija?
Za racionalno funkcijo moraš izračunati ničle, pole, vodoravno/poševno asimptoto, začetno vrednost, ekstreme (ko poznaš odvode).
Za racionalno funkcijo moraš izračunati ničle, pole, vodoravno/poševno asimptoto, začetno vrednost, ekstreme (ko poznaš odvode).

marko181914 ::
Če se ničle ekstremov niso racionalna števila je treba uporabiti bisekcijo. Graf bi na intervalu[0,2] z samo izračunom ničel, pol, asimptot, ekstremov izgledal mal drugače!
Bi izgledal takole: (2x-1)/(x^2+x-2)
Ne pa, tako kot pri tej funkciji.(x^2-2x)/(x^3-3x+2)
Bi izgledal takole: (2x-1)/(x^2+x-2)
Ne pa, tako kot pri tej funkciji.(x^2-2x)/(x^3-3x+2)
lebdim ::
ja, samo marko181914, v tem primeru f(x) = (x2-2x)/(x3-3x+2) sem dobil za odvod f'(x)=(-x4+4x3-3x2+ 4x - 4)/((x3-3x+2)2).
In če pogledaš števec, x4 - 4x3 + 3x2 - 4x + 4 = 0, je ena realna ničla x1=1. Po Hornerju dobim razcep (x - 1)(x3 - 3x2 - 4). Sedaj bi bilo treba še ugotoviti eno ničlo za x3 - 3x2 - 4, ampak ziher ni -1, 2, -2, 4 in -4. Ima pa ta polinom še eno realno ničlo, ker je stopnje 3.
In če pogledaš števec, x4 - 4x3 + 3x2 - 4x + 4 = 0, je ena realna ničla x1=1. Po Hornerju dobim razcep (x - 1)(x3 - 3x2 - 4). Sedaj bi bilo treba še ugotoviti eno ničlo za x3 - 3x2 - 4, ampak ziher ni -1, 2, -2, 4 in -4. Ima pa ta polinom še eno realno ničlo, ker je stopnje 3.

marko181914 ::
Po čem se vidi da graf f(x) = (x2-2x)/(x3-3x+2) v intervalu [1,2] prihaja od spodaj. Po čem se vidi da s graf v intervalu [1,2] ne bo začel od zgoraj? Mam (ničlo,pole, asimtoto) samo to me zanima.
lebdim ::
To bi se dalo utemeljiti s poli. Poli te funkcije: x1,2 = 1 in x3 = -2. Ker je pol pri x = 1 sode (stopnje 2) stopnje in zato se funkcija "ne obrne", kot če bi bil lihe stopnje.
To je podobno kot pri funkcijah x-1 in x-2. Če bi si narisal obe funkciji, bi videl razliko. Tukaj pri tvojem primeru je isto.
To je podobno kot pri funkcijah x-1 in x-2. Če bi si narisal obe funkciji, bi videl razliko. Tukaj pri tvojem primeru je isto.
Zgodovina sprememb…
- spremenil: lebdim ()
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Racionalne funkcijeOddelek: Šola | 1425 (1318) | lebdim |
| » | Matematika kompozitum funkcijOddelek: Šola | 2755 (2520) | lebdim |
| » | Funkcije (strani: 1 2 )Oddelek: Šola | 9617 (8705) | Math Freak |
| » | Graf polinoma & racionalne funkcije.Oddelek: Šola | 3002 (2727) | Math Freak |
| » | Matematično vprašanje (strani: 1 2 )Oddelek: Šola | 12745 (10811) | joze67 |