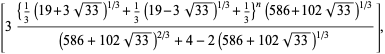Forum » Programiranje » Pomoč pri algoritmu kombinatorike
Pomoč pri algoritmu kombinatorike
xsenon ::
a ima kdo idejo kako naj bi izgledala matematična formula za rešitev spodnjega problema? Sam sem se zadeve lotil v smeri binomskega sibola, vendar zaekrat dokaj neuspešno.
Prehoditi želite n stopnic. Korak lahko naredite na sledeče načine: stopnico za stopnico, dve stopnici naenkrat ali tri stopnice naenkrat. Primer: 4 stopnice lahko prehodite na 7 načinov (1111, 112, 121, 211, 22, 13, 31), 15 stopnic pa na 5768 nacinov.
Prehoditi želite n stopnic. Korak lahko naredite na sledeče načine: stopnico za stopnico, dve stopnici naenkrat ali tri stopnice naenkrat. Primer: 4 stopnice lahko prehodite na 7 načinov (1111, 112, 121, 211, 22, 13, 31), 15 stopnic pa na 5768 nacinov.
etpot - Exploit The Power Of Technology
xsenon ::
to je to kar iščem:) Samo nisem pa še nikl slišal za tribonači zaporedje. No vse je enkrat prvič:) Tnx za pomoč. Zdej pa veselo sprogramirat zadevo
etpot - Exploit The Power Of Technology
hobbit ::
xsenon=)
Algoritem:
public static int tribonaci(int n)
{
if(n==0)
return 0;
else if (n==1)
return 1;
else if(n==2)
return 2;
else if(n==3)
return 4;
else
return (tribonaci(n-1) + tribonaci(n-2) + tribonaci(n-3));
}
Kakšno naključje da imava isto domačo nalogo =)
Algoritem:
public static int tribonaci(int n)
{
if(n==0)
return 0;
else if (n==1)
return 1;
else if(n==2)
return 2;
else if(n==3)
return 4;
else
return (tribonaci(n-1) + tribonaci(n-2) + tribonaci(n-3));
}
Kakšno naključje da imava isto domačo nalogo =)
Zgodovina sprememb…
- spremenil: hobbit ()
xsenon ::
mislm da nisva edina tule z isto domačo nalogo:). Tut moja rešitev je podobna tvoji. Sej k maš rešeno zaporedje (matematično) potem je vse skupi kr izi:)
etpot - Exploit The Power Of Technology
Zgodovina sprememb…
- spremenil: xsenon ()
Fave ::
@hobbit: ni mi všeč tvoj algoritem. Po logiki, ki jo je predstavil xsenon bi bilo takole:
3 stopnice (111,12,21) -> trije načini
2 stopnici (11) -> en način
1 stopnica () -> nič načinov
Popravita me, če se motim.
3 stopnice (111,12,21) -> trije načini
2 stopnici (11) -> en način
1 stopnica () -> nič načinov
Popravita me, če se motim.
My mind's a hyper tool that fixes everything.
xsenon ::
3 stopnice (111,12,21) -> trije načini
2 stopnici (11) -> en način
1 stopnica (1) -> 1 način -> ker narediš samo 1 korak da prideš na stopnico
2 stopnici (11) -> en način
1 stopnica (1) -> 1 način -> ker narediš samo 1 korak da prideš na stopnico
etpot - Exploit The Power Of Technology
Fave ::
hmm, ne vem no....tole mi ni najbolj všeč, ker po tej logiki bi moral imeti pri dveh stopnicah še opcijo 2 in pri treh 3, itn.
Lahko pa, da se motim.
Lahko pa, da se motim.
My mind's a hyper tool that fixes everything.
hobbit ::
Fave, saj jaz sem upošteval da imaš pri dveh stopnicah opcijo 2 in pri treh opcijo 3....algoritem deluje pravilno
Fave ::
Hobbit, zakaj potem pri xsenonovem primeru s štirimi stopnicami ni upoštevana opcija 4?
My mind's a hyper tool that fixes everything.
xsenon ::
zakaj opcija 4? Opcija 4 ne obstaja, opcije, ki jih lahko prehodiš so:
-po 1 stopnico
-po 2 stopnice
-po 3 stopnice
se pravi da pri 4 stopnicah greš lahko 1111, 22, 211, 31,13,121,112 in je rezultat 7.
-po 1 stopnico
-po 2 stopnice
-po 3 stopnice
se pravi da pri 4 stopnicah greš lahko 1111, 22, 211, 31,13,121,112 in je rezultat 7.
etpot - Exploit The Power Of Technology
xsenon ::
ker lahko stopiš 3 štenge naenkrat. se praavi 3 štenge lahko prehodiš:
-tako da stopiš na vsako (111)
-tako da stopiš najprej 2 nato 1 (21)
-tako da stopiš najprej 1 nato 2 (12)
-tako da stopi takoj na tretjo (3), ker imaš možnost stopit največ tri naenkrat
-tako da stopiš na vsako (111)
-tako da stopiš najprej 2 nato 1 (21)
-tako da stopiš najprej 1 nato 2 (12)
-tako da stopi takoj na tretjo (3), ker imaš možnost stopit največ tri naenkrat
etpot - Exploit The Power Of Technology
DavidJ ::
če je n < 0, potem T(n) = 0, sicer
n / T(n)
--------
0 1 (Vprašajte se, zakaj je 0! = 1 ali x^0 = 1.)
1 1
2 2
3 4
T(n) = T(n - 1) + T(n - 3) + T(n - 3)
Rodovna funkcija je G(z) = z / (1 - z - z^2 - z^3)
Sklenjena oblika pa zelooo grda.
n / T(n)
--------
0 1 (Vprašajte se, zakaj je 0! = 1 ali x^0 = 1.)
1 1
2 2
3 4
T(n) = T(n - 1) + T(n - 3) + T(n - 3)
Rodovna funkcija je G(z) = z / (1 - z - z^2 - z^3)
Sklenjena oblika pa zelooo grda.
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
Zgodovina sprememb…
- spremenil: DavidJ ()
xsenon ::
naltel sem še na en izziv in sicer ta je bl verjetnostne narave:
zanima me kako izračunati sledeče.
za šankom sedijo tri dekleta, vsaki izmed deklet damo svojo telefonsko številko. Verjetnost da nas bo poklicala prva je 0.3 , verjetnost da nas bo poklicala druga je 0.8 , verjetnost da nas bo poklicala tretja je 0,7. Kolikšna je verjetnost da nas bo poklicala vsaj ena izmed njih?
Sem računav na vse možne načine vendar ne pridem do pravilnega rezultata. (pravilni rezultat je 0.96).
zanima me kako izračunati sledeče.
za šankom sedijo tri dekleta, vsaki izmed deklet damo svojo telefonsko številko. Verjetnost da nas bo poklicala prva je 0.3 , verjetnost da nas bo poklicala druga je 0.8 , verjetnost da nas bo poklicala tretja je 0,7. Kolikšna je verjetnost da nas bo poklicala vsaj ena izmed njih?
Sem računav na vse možne načine vendar ne pridem do pravilnega rezultata. (pravilni rezultat je 0.96).
etpot - Exploit The Power Of Technology
DavidJ ::
1 - P(ne pokliče nobena) = 1 - (1-0.3)*(1-0.8)*(1-0.7) = 0.96
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | led osvetlitev stopnišča (strani: 1 2 )Oddelek: Loža | 26618 (22236) | Map |
| » | Vaje za odriv ! (strani: 1 2 )Oddelek: Loža | 21940 (11176) | STU-III |
| » | Digitalna evolucija (strani: 1 2 3 4 … 26 27 28 29 )Oddelek: Znanost in tehnologija | 79919 (30088) | pietro |
| » | Neskončna majhnostOddelek: Znanost in tehnologija | 1774 (1774) | SavoKovac |
| » | [Java] Liha potencaOddelek: Programiranje | 2042 (1936) | bijonda |