Slo-Tech - Eden izmed najprivlačnejših matematičnih problemov, katerega rešitev bi pomembno vplivala na tudi na računalništvo, je vprašanje ali je P enako NP. Gre za enega izmed sedmih tako imenovanih tisočletnih problemov v matematiki, z rešitvijo katerega lahko od Clay Mathematics Instituta dobimo milijon dolarjev nagrade (kar je nekoliko več od Nobelove nagrade). Doslej je bil rešen samo eden izmed sedmerice problemov. Problem P proti NP sprašuje, ali za vsak problem, katerega rešitev lahko preverimo v polinomskem času, v polinomskem času tudi rešimo. O tovrstnih vprašanjih so se pogovarjali že Nash, Gödel in von Neumann, rigorozno formulacijo pa je leta 1971 postavil Stephen Cook.

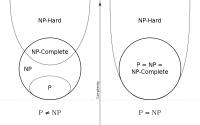
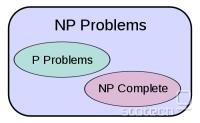
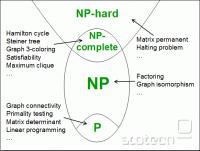
Trenutno prevladujoče mnenje v znanosti je, da velja P ≠ NP...

Slo-Tech - Minuli teden je medije preplavilo sporočilo, da je nigerijski matematik Opeyemi Enoch rešil 150 let star matematični problem, ki sodi med sedem največjih nerešenih matematičnih problem, ki vsak prinaša milijon dolarjev za rešitev. Trdi, da je dokazal Riemannovo hipotezo. Doslej nagrade še niso podelili, čeprav je bil en problem že rešen. Tedaj nagrade niso podelili, ker je ekscentrični ruski matematik Grigorij Pereljman ni želel prevzeti, to pot pa kaže, da Enochu ni uspelo dokazati Riemannove hipoteze. In ne bi bil prvi.

Nerešenih milenijskih problemov, ki jih je razpisal Clay Mathematics Institute of Cambridge iz Massachusettsa, je še šest, a Riemannova hipoteza je gotovo med najbolj znanimi. Riemannova hipoteza pravi, da...

Slo-Tech - Prejšnji teden je bil nadpovprečno pester v svetu analitične teorije števil. Najprej smo dobili prvo zgornjo mejo pri iskanju dokaza o obstoju neskončno mnogo praštevilskih dvojčkov, sedaj pa še bistveno pomembnejši rezultat. Perujski matematik Harald Helfgott je namreč objavil dopolnitev svojega članka, s čimer je - najverjetneje - dokazal šibko Goldbachovo domnevo (uradno preverjanje dokaza še čaka, a na prvi pogled v njem ni nedoslednosti ali napak).

Torej, Goldbachova domneva je eden izmed najbolj elegantnih, najstarejših in očitno tudi najtežjih matematičnih problemov....

Slashdot - Propadel je še en poizkus dokaza slavnega problema P = NP?, za katerega je razpisana nagrada milijon dolarjev in ki vprašuje, ali so vsi problemi, za katere je moč dane rešitve preveriti v polinomskem času, tudi rešljivi enako hitro. Ruski matematik Vladimir Romanov je svoj dokaz objavil januarja letos in na prvi pogled je kazalo, da utegne biti korekten. Izkazalo se je, da milijona dolarjev še ne bo dobil.

Napako je v dokazu po enomesečnem seciranju priznal kar sam avtor, a puške še ni vrgel v koruzo. Zapisal je namreč tudi, da dokaz potrebuje dopolnilo in namignil, da ga bo predložil. Za zdaj pa dodajamo njegov dokaz v dolgo vrsto neuspelih poizkusov, ki smo jih zadnjih 30 let videli že nekaj.

Problem si lahko v tipični slovenski maniri...

Slo-Tech - Ruski matematik Vladimir Romanov je naslednji v vrsti znanstvenikov, ki predstavljajo svoj poizkus dokaza milenijskega matematičnega problema, ali je P enako NP. Lani je k temu resno pristopil Vinay Deolalikar, a je bil njegov poizkus neuspešen. Problem P = NP vprašuje, ali lahko vsak problem z v polinomskem času preverljivo rešitvijo enako hitro tudi rešimo. Zdi se, da to ne drži, a v matematiki slutnje in domneve bolj malo štejejo.

Romanov je objavil članek z naslovom Non-Orthodox Combinatorial Models Based on Discordant Structures, v katerem predstavlja algoritem za rešitev problema 3-sat v polinomskem času. Ker je 3-sat NP-poln problem, bi bil to že dokaz, da velja P = NP. V...

Slo-Tech - Relativno neznani matematik Vinay Deolalikar, ki je zaposlen v Hewlett-Packardu, je prejšnji konec tedna osupnil svet s povsem resno objavo, da je dokazal milenijski matematični problem, da P ni NP. Domnevni dokaz obsega 102 strani in ni le potegavščina, marveč zaresen poizkus dokaza tega problema. Žal po nekaj dneh pregledovanja internetne skupnosti lahko skoraj gotovo zaključimo, da neuspešen.

Clay Mathematics Institute of Cambridge iz Massachusettsa je na prelomu tisočletja razpisal nagrado milijon dolarjev za rešitev vsakega izmed sedmih največjih nerešenih (poimenovanih milenijski) problemov v matematiki. Ti so Swinnerton-Dyerjeva domneva, Hodgeova domneva, Navier-Stokesove enačbe, problem P = NP, Riemannova hipoteza,

Washington Post - Marca smo pisali o matematičnem geniju iz Rusije Grigoriju Jakovljeviču Pereljmanu, ki je leta 2003 predložil dokaz Poincaréjeve domneve. Rešitev se je po natančni preveritvi izkazala za korektno in ker sodi med sedem matematičnih problemov tisočletja, kot jih je opredelil Clay Mathematics Institute of Cambridge, pripada Pereljmanu nagrada v vrednosti milijon dolarjev. Svojo ekscentričnost je Pereljman dokazal že večkrat, saj na primer ni sprejel Fieldsove medalje...

The New York Times - Clay Mathematics Institute of Cambridge iz Massachusettsa je na prelomu tisočletja razpisal nagrado milijon dolarjev za rešitev vsakega izmed sedmih največjih nerešenih (poimenovanih milenijski) problemov v matematiki. Ti so Swinnerton-Dyerjeva domneva, Hodgeova domneva, Navier-Stokesove enačbe, problem P = NP, Riemannova hipoteza, Yang-Millsova teorija in Poincaréjeva domneva. Slednjo je leta 1904 postavil francoski matematik Henri Poincaré in predstavlja topološki problem. V topologiji velja, da je 2-sfera enostavno povezano območje, kar pomeni, da je povezano s potmi in da lahko...

Slo-Tech - Intel je izdal nove prevajalnike (C++ in Fortran) za Windows in Linux. Za Windows so na voljo 30-dnevne preizkusne različice, potem pa je treba seči v žep, medtem ko za Linux lahko dobimo nekomercialno in nepodprto verzijo zastonj. Še dokaz: http://developer.intel.com/software/pro... Kdaj točno so objavili nove verzije, ne vem, kakšna dva meseca nazaj je bila aktualna verzija 5.01 tako za C++ kot za Fortran.