Slo-Tech - Ruski matematik Vladimir Romanov je naslednji v vrsti znanstvenikov, ki predstavljajo svoj poizkus dokaza milenijskega matematičnega problema, ali je P enako NP. Lani je k temu resno pristopil Vinay Deolalikar, a je bil njegov poizkus neuspešen. Problem P = NP vprašuje, ali lahko vsak problem z v polinomskem času preverljivo rešitvijo enako hitro tudi rešimo. Zdi se, da to ne drži, a v matematiki slutnje in domneve bolj malo štejejo.
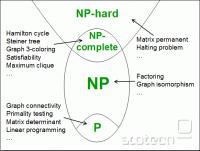
Romanov je objavil članek z naslovom Non-Orthodox Combinatorial Models Based on Discordant Structures, v katerem predstavlja algoritem za rešitev problema 3-sat v polinomskem času. Ker je 3-sat NP-poln problem, bi bil to že dokaz, da velja P = NP. V podporo svojemu dokazu je objavil tudi izvorno kodo algoritma.
Spletni komentarji za zdaj kažejo, da bo ta poizkus dokaza doletela enaka usoda kot predhodne. Že v nekaj dneh bo jasno, ali ima za dokaz resne možnosti, da bi obveljal.
Novice » Znanost in tehnologija » Predstavljen poizkus dokaza P = NP
Thomas ::
Ne verjamem, da N=NP. Če bi rekel, da je morda dokazal N!=NP, potem bi mu bolj verjel.
Man muss immer generalisieren - Carl Jacobi
andraz2112 ::
Thomas ::
It would just be too easy.
Če bi jaz koval dokaz, da P!=NP sevedA, potem bi ... imam ene ideje, kako bi to šlo. Samo ne bom pravil, če ne dokažem. Dokazal pa ne bom, ker niti ne dokazujem.
Če mi iz modrega neba blisne, potem pa že mogoče.
Samo mi ne bo.
Najverjetneje.
Pustmo stat!
Če bi jaz koval dokaz, da P!=NP sevedA, potem bi ... imam ene ideje, kako bi to šlo. Samo ne bom pravil, če ne dokažem. Dokazal pa ne bom, ker niti ne dokazujem.
Če mi iz modrega neba blisne, potem pa že mogoče.
Samo mi ne bo.
Najverjetneje.
Pustmo stat!
Man muss immer generalisieren - Carl Jacobi
Zero0ne ::
Posledice odkritja P == NP bi bile v resnici veliko milejše, kot predvidevajo nekateri (slashdot: AES razbit, nebo pada!!!1). Tudi enkripcijski sistemu, ki temeljijo na NP-popolnosti, bi lahko samo podaljšali enkripcijske ključe za red velikosti, in bi bili še kakšno desetletje nepremagljivi tudi za napade, ki se poslužujejo na P==NP temelječih algoritmov. Do takrat pa bo vse, kar danes vemo o računalniški znanosti antična zgodovina.
uname -o
Jst ::
Brca (najverjetneje) v temo: Kaj pa quantum-based algoritmi?
Islam is not about "I'm right, you're wrong," but "I'm right, you're dead!"
-Wole Soyinka, Literature Nobelist
|-|-|-|-|Proton decay is a tax on existence.|-|-|-|-|
-Wole Soyinka, Literature Nobelist
|-|-|-|-|Proton decay is a tax on existence.|-|-|-|-|
fiction ::
Brca (najverjetneje) v temo: Kaj pa quantum-based algoritmi?Wikipedia pravi da ti to prav nič ne pomaga pri reševanju NP-polnih problemov. Moje mnenje je, da pač s kvantnim računalnikom (če to ne bi bil bolj ko ne PoC) lahko počneš stvari izredno hitro - saj vse "staličiš" v en qubit in potem z njim čaraš. Ampak problem je pa na koncu: kako prebrati rezultat, ker z meritvijo vse uničiš. Dokaz, da je BQP večji kot BPP je pomoje ravno Shorov algoritem s katerim se da število faktorizirati v polinomskem času.
fiction ::
Meni se zdi tudi bolj intuitivno, da P != NP. Argument za to je nekako, da obstaja kar nekaj praktično uporabnih NP-polnih problemov za katere je že sigurno kdo razmišljal o njihovi optimizaciji (tako da bi jih rešil točno v polinomskem času), ampak nobeden še ni prišel z rešitvijo in tako ni še nihče dokazal P = NP. Vse skupaj jasno ni dokaz (da nekaj ni bilo dokazano še ne pomeni, da mora veljati nasprotno), le za občutek...
Mogoče bo pa zdaj dokazano da P = NP. Pri tem članku me je malo strah, da bo nekje iz ozadja skočila ena 2^n, ki je avtor ni upošteval in bo vse šlo k vragu.
Mogoče bo pa zdaj dokazano da P = NP. Pri tem članku me je malo strah, da bo nekje iz ozadja skočila ena 2^n, ki je avtor ni upošteval in bo vse šlo k vragu.
Jst ::
fiction: Ja, točno to sem tudi sam mislil. Da bi morda lahko z kvantno mehaniko dokazali, da P != NP. Malo sem brskal po scholar.google in je tega materiala res veliko, vendar nisem našel nič konkretnega. Zato sem pa tukaj vprašal za "drugo" mnenje.
Islam is not about "I'm right, you're wrong," but "I'm right, you're dead!"
-Wole Soyinka, Literature Nobelist
|-|-|-|-|Proton decay is a tax on existence.|-|-|-|-|
-Wole Soyinka, Literature Nobelist
|-|-|-|-|Proton decay is a tax on existence.|-|-|-|-|
Thomas ::
AFAIK, QM ni "trans", v tem smislu, da bi si z njo lahko kaj dosti pomagali. Kar je težko za navaden računalnik, je težko tudi za kvantnega.
Tudi zato mislim, da s "kvantnim prijemom" za ta problem, ne bo kruha.
Tudi zato mislim, da s "kvantnim prijemom" za ta problem, ne bo kruha.
Man muss immer generalisieren - Carl Jacobi
poweroff ::
[-----
Lisica bi tudi jedla grozdje, če ne bi bilo ... kislo.
Če bi jaz koval dokaz, da P!=NP sevedA, potem bi ... imam ene ideje, kako bi to šlo. Samo ne bom pravil, če ne dokažem. Dokazal pa ne bom, ker niti ne dokazujem.
Lisica bi tudi jedla grozdje, če ne bi bilo ... kislo.
sudo poweroff
Zgodovina sprememb…
- spremenilo: gzibret ()
Thomas ::
Lisica bi tudi jedla grozdje, če ne bi bilo ... kislo.
Narobe. Lisica bi kuro ali petelina. Grozdje naj pokavsata pa kar onadva.
Man muss immer generalisieren - Carl Jacobi
gzibret ::
Napake v novici so popravljene, zato izbrisani komentarji niso več potrebni. Hvala vseeno za opozorilo. Sedaj pa nazaj ontopic.
Vse je za neki dobr!
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Problem P = NP ostaja nerešen (strani: 1 2 )Oddelek: Novice / Znanost in tehnologija | 22465 (17973) | reeves |
| » | Januarski poizkus dokaza problema P = NP neuspešenOddelek: Novice / Znanost in tehnologija | 4748 (3284) | Thomas |
| » | Predstavljen poizkus dokaza P = NPOddelek: Novice / Znanost in tehnologija | 7887 (6116) | gzibret |
| » | Problem P ≠ NP za zdaj ostaja nerešenOddelek: Novice / Znanost in tehnologija | 9877 (6713) | pecorin |