Forum » Šola » Langragian - gibalne enačbe
Langragian - gibalne enačbe
marjan_h ::
To sicer še ni Langragian, vendar pridemo do tja:
Če vzamemo najprej preprost primer uteži na vzmeti. Pa zapišemo:
ma = -kx
Desni del je Hookov zakon. Vendar mi ni jasno čisto, zakaj damo minus predtem. Če nekaj raztegnemo na vzmeti, potem gre ta stvar navzdol in navzgor. Kar pomeni v pozitivno (x) smer in negativno. Razen, če tukaj vzamemo najvišjo lego kot 0. In vse kar je navzdol je negativna smer?
Rešitev te navadne diferencialne enačbe je:
omega = sqrt(m/k)
Kaj pomeni ta rezultat? To vstavimo nazaj v cos(omega*t + phi)?
Če vzamemo najprej preprost primer uteži na vzmeti. Pa zapišemo:
ma = -kx
Desni del je Hookov zakon. Vendar mi ni jasno čisto, zakaj damo minus predtem. Če nekaj raztegnemo na vzmeti, potem gre ta stvar navzdol in navzgor. Kar pomeni v pozitivno (x) smer in negativno. Razen, če tukaj vzamemo najvišjo lego kot 0. In vse kar je navzdol je negativna smer?
Rešitev te navadne diferencialne enačbe je:
omega = sqrt(m/k)
Kaj pomeni ta rezultat? To vstavimo nazaj v cos(omega*t + phi)?
kljuka13 ::
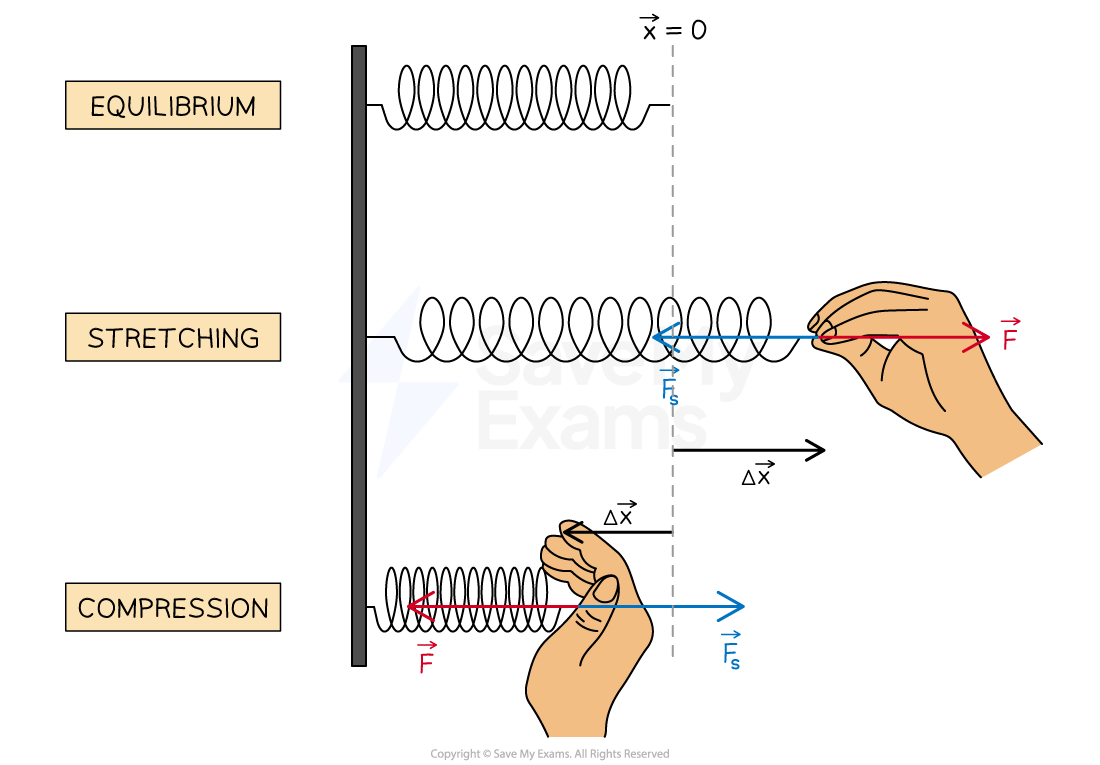
Minus se v enačbi pojavi zato, ker sila vzmeti kaže v nasprotno smer, kot jo raztegnemo oziroma skrčimo. Da ne mede gravitacija, si raje predstavljaj vzmet na vodoravni podlagi, ki je na levi strani pritrjena na steno. Če sedaj drugi konec vzmeti povlečeš v desno (in s tem vzmet raztegneš), bo sila vzmeti delovala v levo (vlekla tvojo roko proti steni). Če pa konec vzmeti potisneš v levo (in s tem vzmet skrčiš), bo sila vzmeti delovala v desno (tvojo roko bo potiskala stran od stene). Smer sile vzmeti je torej zmeraj v nasprotno smer, kot je njen raztezek, in to v enačbi opisuje minus.
Pri vzmeti z lego 0 označujemo tisto lego, v kateri je vzmet neobremenjena (torej niti raztegnjena niti skrčena).
Tukaj še slika za lažjo predstavo. Z modro puščico Fs je označena sila vzmeti.
In zdaj na rešitev gibalne enačbe. Kar si napisal, ni zares rešitev, ampak zgolj parameter rešitve. Celotna rešitev se glasi: x(t) = x0 cos(omega t + delta), pri čemer je, kot si napisal, omega = sqrt(k/m) (pozor, napačno si zapisal obratno vrednost!). Ta zapisana rešitev pove, kako se spreminja lega uteži s časom. Spreminja se tako, da niha okoli ravnovesne lege, pri čemer je krožna frekvenca nihanja omega. Fizikalni uvid, ki nam da ta parameter, je takšen: če želimo frekvenco nihanja vzmeti povečati za dvakrat, moramo bodisi povečati konstanto vzmeti za štirikrat bodisi zmanjšati maso uteži za štirikrat.
Pri vzmeti z lego 0 označujemo tisto lego, v kateri je vzmet neobremenjena (torej niti raztegnjena niti skrčena).
Tukaj še slika za lažjo predstavo. Z modro puščico Fs je označena sila vzmeti.
In zdaj na rešitev gibalne enačbe. Kar si napisal, ni zares rešitev, ampak zgolj parameter rešitve. Celotna rešitev se glasi: x(t) = x0 cos(omega t + delta), pri čemer je, kot si napisal, omega = sqrt(k/m) (pozor, napačno si zapisal obratno vrednost!). Ta zapisana rešitev pove, kako se spreminja lega uteži s časom. Spreminja se tako, da niha okoli ravnovesne lege, pri čemer je krožna frekvenca nihanja omega. Fizikalni uvid, ki nam da ta parameter, je takšen: če želimo frekvenco nihanja vzmeti povečati za dvakrat, moramo bodisi povečati konstanto vzmeti za štirikrat bodisi zmanjšati maso uteži za štirikrat.
Zgodovina sprememb…
- spremenil: kljuka13 ()
JanK ::
Odlicna razlaga! Naj dodam se to, da je krozna frekvenca odvisna od korena parametrov nihanja pri vseh harmonicnih oscilatorjih. To so tisti, kjer je sila, ki vraca nihajoci del nihala v mirovno lego, linearno odvisna od odmika od mirovne lege. To pride iz dvojnega odvajanja v diferencialni enacbi, kar prinese \omega^2, ostali faktorji pa ostanejo. In ko poracunas, vedno dobis koren.
- Pri nitnem nihalu sqrt(m/l), 4x daljse za 2x pocasnejse nihanje
- Pri sucnem nihalu (v mehanski rocni uri) \sqrt(J/K), kjer je J vztrajnosti moment, K pa konstanta spiralne vzmeti
- Celo pri kvantnem harmonicnem oscilatorju je \omega = \sqrt(k/m). Le da lahko klasicno nihalo niha s poljubno majhno amplitudo (dokler ne postane kvantno :), v kvantnem svetu pa so energijski nivoji diskretni: $E_n = \hbar \omega(n + 1/2).
- Pri nitnem nihalu sqrt(m/l), 4x daljse za 2x pocasnejse nihanje
- Pri sucnem nihalu (v mehanski rocni uri) \sqrt(J/K), kjer je J vztrajnosti moment, K pa konstanta spiralne vzmeti
- Celo pri kvantnem harmonicnem oscilatorju je \omega = \sqrt(k/m). Le da lahko klasicno nihalo niha s poljubno majhno amplitudo (dokler ne postane kvantno :), v kvantnem svetu pa so energijski nivoji diskretni: $E_n = \hbar \omega(n + 1/2).
"Think about how stupid the average person is,
then realize that 50% are stupider than that"
-George Carlin
then realize that 50% are stupider than that"
-George Carlin
marjan_h ::
Hvala obema.
Me pa še zanima pri Newtonovi mehaniki. Kako narediš bolj zapletene primere? Pa potem gremo na Langrangiana.
Recimo če imamo vzmet na vzmet?
ma = -kx + -kx?
Me pa še zanima pri Newtonovi mehaniki. Kako narediš bolj zapletene primere? Pa potem gremo na Langrangiana.
Recimo če imamo vzmet na vzmet?
ma = -kx + -kx?
kljuka13 ::
Princip je v splošnem zmeraj enak. Najprej si izbereš opazovano telo, določiš vse zunanje sile, ki delujejo na to telo, in izračunaš njihovo rezultanto, torej vektorsko vsoto vseh zunanjih sil. Za tem uporabiš 2. Newtonov zakon, ki poveže rezultanto zunanjih sil s pospeškom telesa. Primer uteži na vzmeti je relativno preprost, ker deluje na telo zgolj ena sila. Dodaj več sil, pa boš dobil bolj zapleten primer.
Če želiš ostati pri gibanju v eni dimenziji, si zamisli gibanje frnikole v medu. Na frnikolo delujejo tri poglavitne sile: teža, vzgon in upor. Diferencialna enačba, ki jo pridelaš, se glasi:
m a = m g - rho V g - 6 pi eta r v,
pri čemer je m masa frnikole, r njen polmer in V njena prostornina, rho gostota medu in eta njegova viskoznost.
Kar zadeva uteži, ki je pripeta na dve zaporedno vezani vzmeti, pa je to ekvivalenten primer kot utež na eni vzmeti, katere konstanta vzmeti je pol tolikšna kot konstanta posamezne vzmeti (če sta enaki).
Če želiš ostati pri gibanju v eni dimenziji, si zamisli gibanje frnikole v medu. Na frnikolo delujejo tri poglavitne sile: teža, vzgon in upor. Diferencialna enačba, ki jo pridelaš, se glasi:
m a = m g - rho V g - 6 pi eta r v,
pri čemer je m masa frnikole, r njen polmer in V njena prostornina, rho gostota medu in eta njegova viskoznost.
Kar zadeva uteži, ki je pripeta na dve zaporedno vezani vzmeti, pa je to ekvivalenten primer kot utež na eni vzmeti, katere konstanta vzmeti je pol tolikšna kot konstanta posamezne vzmeti (če sta enaki).
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | fizika nalogaOddelek: Šola | 2206 (1988) | onitam |
| » | Fizika - NalogaOddelek: Šola | 2720 (2498) | Wisse |
| » | nitno nihaloOddelek: Šola | 1968 (1731) | amacar |
| » | Toshiba z novim 2,5" diskomOddelek: Novice / Diski | 5118 (4300) | MrStein |
| » | fizikaOddelek: Šola | 2261 (1918) | sidd |