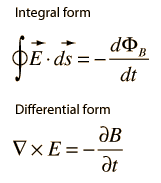Forum » Šola » E*ds
E*ds
marjan_h ::
Zakaj je inducirana napetost E*ds, ki izhaja iz Faradayevega zakona?:
Torej, če vzamemo poljubno električno polje in gremo po neki zaključeni poti s znotraj tega polja, potem bomo dobili električno napetost v zanki, npr. če priključimo voltmeter na zanko?
Je nekako tako? Ker ne razumem zakaj.
Torej, če vzamemo poljubno električno polje in gremo po neki zaključeni poti s znotraj tega polja, potem bomo dobili električno napetost v zanki, npr. če priključimo voltmeter na zanko?
Je nekako tako? Ker ne razumem zakaj.
stapler rump ::
Torej, če vzamemo poljubno električno polje in gremo po neki zaključeni poti s znotraj tega polja, potem bomo dobili električno napetost v zanki
Res je, če misliš s tem inducirano napetost v zanki. Če ni spreminjajočega magnetnega polja je integral po zaključeni poti 0 (in s tem inducirana napetost enaka 0)
npr. če priključimo voltmeter na zanko?
Pri idealnem voltmetru in zanki, da.
Zakaj je inducirana napetost E*ds
Mogoče ne razumem, kaj točno sprašuješ.
Zakaj krivuljni integral električnega polja? Zato ker je to definicija napetosti (inducirane ali kake druge) Na tak način se lahko inducirano napetost obravnava podobno kot npr. napetost baterije.
Zakaj je tak integral enak časovnemu odvodu magnetnega pretoka skozi zanko? Iz vprašanja sklepam, da študiraš za Osnove elektrotehnike ali kak podoben predmet. V tem primeru je odgovor zate bolj ali manj "ker tako deluje naše vesolje". Gre pač za enega od naravnih zakonov. Podobno, kot bi pri mehaniki vprašal zakaj je pospešek telesa odvisen od mase in sile: to je model, ki najboljše napove rezultate naših eksperimentov.
Malo bolj podroben odgovor se skriva v relativistični obravnavi elektromagnetnega polja, ki ti pove povezavo med magnetizmom in električnim poljem. Če te to zanima poglej v kak učbenik o posebni teoriji relativnosti, ampak na koncu te poti te spet čaka bolj ali manj enak odgovor kot zgoraj.
Unilseptij ::
Prva enačba pravi, da se v poljubni zanki, skozi katero opazujemo magnetni pretok, inducira električno polje, katerega integral po sklenjeni poti zanke je enak spremembi magnetnega pretoka (skozi zanko) v času, torej hitrosti naraščanja ali upadanja magnetnega pretoka. Bistvo je torej spreminjanje mag. polja skozi zanko, kar inducira napetost v zanki. Neničelni integral el. polja po sklenjeni zanki pomeni, da skozi tako zanko steče tok, z voltmetrom pa bi izmeril padec napetosti med dvema točkama zanke. Vrednost levega integrala ni dejanska napetost, ki jo lahko izmeriš, ampak celotni el. potencial, ki poganja inducirani tok skozi zanko. Izmeriš pa pač napetost na nekem delu zanke, ki je sorazmerni del celotne potencialne razlike v zanki, pač glede na to, kje pritakneš voltmeter.
Druga enačba je ekvivalentna prvi, le da je v diferencialni obliki, levi del pa pomeni vrtinčenje (rotor) el. polja v smislu, da se njegova smer spreminja, tako da v sklenjeni zanki linijski integral ni nič. To je bistvena razlika, saj je brez indukcije električno polje vedno brezvrtinčno in za napetost vedno rabimo neko razliko v količini el. naboja med točkama, kjer merimo. Silnice el. polja potekajo od pozitivnega do negativnega naboja, pri indukciji pa potekajo po zanki.
Druga enačba je ekvivalentna prvi, le da je v diferencialni obliki, levi del pa pomeni vrtinčenje (rotor) el. polja v smislu, da se njegova smer spreminja, tako da v sklenjeni zanki linijski integral ni nič. To je bistvena razlika, saj je brez indukcije električno polje vedno brezvrtinčno in za napetost vedno rabimo neko razliko v količini el. naboja med točkama, kjer merimo. Silnice el. polja potekajo od pozitivnega do negativnega naboja, pri indukciji pa potekajo po zanki.
Zgodovina sprememb…
- spremenilo: Unilseptij ()
stapler rump ::
Neničelni integral el. polja po sklenjeni zanki pomeni, da skozi tako zanko steče tok, z voltmetrom pa bi izmeril padec napetosti med dvema točkama zanke. Vrednost levega integrala ni dejanska napetost, ki jo lahko izmeriš, ampak celotni el. potencial, ki poganja inducirani tok skozi zanko. Izmeriš pa pač napetost na nekem delu zanke, ki je sorazmerni del celotne potencialne razlike v zanki, pač glede na to, kje pritakneš voltmeter.
To je narobe. Ta enačba nič ne govori o električnem toku. Zanka po kateri se integrira je lahko v vakuumu, zraku ali čem drugem. Tok lahko teče ali pa ne, pa bo še vedno integral električnega polja enak odvodu magnetnega pretoka. Če po zanki položiš idealno prevoden material in v eni točki zanko prekineš in vanjo vstaviš idealen voltmeter, bo ta pokazal vrednost integrala, čeprav po zanki ne bo tekel noben tok (ker ima idealen voltmeter neskončno veliko upornost).
za napetost vedno rabimo neko razliko v količini el. naboja med točkama, kjer merimo.
Napetost med točkama v splošnem ni povezana z količino naboja na teh točkah.
marjan_h ::
Tukaj sta E in ds vektorja.
Nato skalarno zmnožimo vektorja. Če sta vektorja pravokotna je skalarni produkt enak 0.
Kar pomeni, da nič ne prispeva k inducirani napetosti v zanki. Vendar si to težko predstavljam. Zakaj je vektor E in vektor poti, če sta pravokotna je inducirana napetost 0?
Nato skalarno zmnožimo vektorja. Če sta vektorja pravokotna je skalarni produkt enak 0.
Kar pomeni, da nič ne prispeva k inducirani napetosti v zanki. Vendar si to težko predstavljam. Zakaj je vektor E in vektor poti, če sta pravokotna je inducirana napetost 0?
Unilseptij ::
stapler rump je izjavil:
Neničelni integral el. polja po sklenjeni zanki pomeni, da skozi tako zanko steče tok, z voltmetrom pa bi izmeril padec napetosti med dvema točkama zanke. Vrednost levega integrala ni dejanska napetost, ki jo lahko izmeriš, ampak celotni el. potencial, ki poganja inducirani tok skozi zanko. Izmeriš pa pač napetost na nekem delu zanke, ki je sorazmerni del celotne potencialne razlike v zanki, pač glede na to, kje pritakneš voltmeter.
To je narobe. Ta enačba nič ne govori o električnem toku. Zanka po kateri se integrira je lahko v vakuumu, zraku ali čem drugem. Tok lahko teče ali pa ne, pa bo še vedno integral električnega polja enak odvodu magnetnega pretoka. Če po zanki položiš idealno prevoden material in v eni točki zanko prekineš in vanjo vstaviš idealen voltmeter, bo ta pokazal vrednost integrala, čeprav po zanki ne bo tekel noben tok (ker ima idealen voltmeter neskončno veliko upornost).
za napetost vedno rabimo neko razliko v količini el. naboja med točkama, kjer merimo.
Napetost med točkama v splošnem ni povezana z količino naboja na teh točkah.
Jah, saj imaš v vsem prav... nejasnosti je treba pripisati mojemu trudu, da poskušam povedati čim bolj preprosto. Zanka je seveda lahko poljubna in fiktivna, ampak s predpostavko, da je prevodna, nič ne izgubimo na splošnosti, ker vedno lahko pač upornost prevodne zanke limitiramo proti neskončnosti. Hotel sem se predvsem izogniti predstavi, da bi voltmeter pokazal nekaj tudi, če sploh ne bi bilo nobene prevodne zanke, kar bi lahko bil zaključek po "tvoji" interpretaciji, in to seveda ni res.
Glede napetosti in količine naboje sem hotel povedati, da je el. polje v primeru, ko ni indukcije, izraženo kot gradient potenciala (=napetosti), v primeru z indukcijo pa to ni mogoče, zato med dvema točkama v zanki ni možno neposredno meriti napetosti... merimo jo lahko samo preko toka, ki kot posledica inducirane napetosti steče po prevodni zanki s končno upornostjo.
Tukaj sta E in ds vektorja.
Nato skalarno zmnožimo vektorja. Če sta vektorja pravokotna je skalarni produkt enak 0.
Kar pomeni, da nič ne prispeva k inducirani napetosti v zanki. Vendar si to težko predstavljam. Zakaj je vektor E in vektor poti, če sta pravokotna je inducirana napetost 0?
E in ds sta vektorja, vendar pa njun skalarni produkt ni nujno nič v vsaki točki zanke, ampak samo v povprečju, ko sešteješ vse skalarne produkte v vseh točkah zanke... od tod linijski integral.
Zgodovina sprememb…
- spremenilo: Unilseptij ()
marjan_h ::
E in ds sta vektorja, vendar pa njun skalarni produkt ni nujno nič v vsaki točki zanke, ampak samo v povprečju, ko sešteješ vse skalarne produkte v vseh točkah zanke... od tod linijski integral.
To razumem, vendar zakaj npr. točka kjer sta vektorja E in s pravokotna ne prispeva k končni napetosti? Torej če bi potovali po poti s, ko bi šli mimo E, kjer sta pravokotna nebi občutili nobene sile?
Ghenghiz ::
E in ds sta vektorja, vendar pa njun skalarni produkt ni nujno nič v vsaki točki zanke, ampak samo v povprečju, ko sešteješ vse skalarne produkte v vseh točkah zanke... od tod linijski integral.
To razumem, vendar zakaj npr. točka kjer sta vektorja E in s pravokotna ne prispeva k končni napetosti? Torej če bi potovali po poti s, ko bi šli mimo E, kjer sta pravokotna nebi občutili nobene sile?
Obcutil bi silo pravokotno na pot (ce bi imel naboj, seveda). Ker si se odlocil drzati poti kot pijanec plota, te zato ta sila ne gane prav nic.
marjan_h ::
Aha, ja to sem malo nerodno vprašal. Mislil sem na napetost. Ker je napetost = delo/naboj.
Nekako želim vedeti zakaj, ko sta vektorja E in s pravokotna ne prispeva nič k končni napetosti?
Sicer pa ne vem, kako se reče če naboj občuti silo zaradi polja, npr. v tem zgornjem primeru.
Nekako želim vedeti zakaj, ko sta vektorja E in s pravokotna ne prispeva nič k končni napetosti?
Sicer pa ne vem, kako se reče če naboj občuti silo zaradi polja, npr. v tem zgornjem primeru.
Unilseptij ::
Nič ne prispeva, ker sila ne opravi nobenega dela. Delo je sila krat pot (skalarni produkt vektorjev) in če je sila pravokotna na pot, potem ne opravi nobenega dela. Tako kot recimo sila teže ne opravlja nobenega dela, če se telo giblje vodoravno.
Ali še z drugimi besedami... sila, ki deluje pravokotno na smer gibanja ne prispeva k spremembi kinetične energije telesa in torej ne opravi nobenega dela.
Ali še z drugimi besedami... sila, ki deluje pravokotno na smer gibanja ne prispeva k spremembi kinetične energije telesa in torej ne opravi nobenega dela.
Ghenghiz ::
Cisto na splosno povedano: polje pove v katero smer in koliko se spreminja potencial. Ce gledas (ali se premikas) v smeri pravokotno na smer polja, se potencial torej ne spreminja. Koncni potencial je sestevek vseh sprememb potenciala - kjer se potencial ne spreminja torej ni prispevka h koncnemu potencialu (in napetost je razlika potenciala).
Lahko si naredis analogijo z gravitacijo, ki si jo pojasnjujemo z enakimi matematicnimi konstrukti: dokler valis kuglo po isti nadmorski visini, se ji potencialna energija ne bo spreminjala - pa sploh ni vazno, ali to delas preko ceste na Alpe d'Huez.
Ce hoces pa bolj "globoko" razlago, pa hitro skocis v matematice definicije (kar je pomojem mnenju ravno nasprotno od globoke razlage, saj na koncu to pomeni odgovor "ker smo se tako zmenili z aksiomi").
Lahko si naredis analogijo z gravitacijo, ki si jo pojasnjujemo z enakimi matematicnimi konstrukti: dokler valis kuglo po isti nadmorski visini, se ji potencialna energija ne bo spreminjala - pa sploh ni vazno, ali to delas preko ceste na Alpe d'Huez.
Ce hoces pa bolj "globoko" razlago, pa hitro skocis v matematice definicije (kar je pomojem mnenju ravno nasprotno od globoke razlage, saj na koncu to pomeni odgovor "ker smo se tako zmenili z aksiomi").
marjan_h ::
hvala, sedaj razumem.
Če se vrnemo še na jakost električnega polja:
Ali je negativni gradient tukaj, zato ker vektor električnega potenciala kaže od pozitivnega naboja do negativnega. V resnici pa je jakost definirana iz plus v minus, in zato je tam pri gradientu minus spredaj?
Če se vrnemo še na jakost električnega polja:
Ali je negativni gradient tukaj, zato ker vektor električnega potenciala kaže od pozitivnega naboja do negativnega. V resnici pa je jakost definirana iz plus v minus, in zato je tam pri gradientu minus spredaj?
Unilseptij ::
El. potencial je skalar, ne vektor. Minus je tam zato, ker po dogovoru sila (el. polje) kaže od višjega potenciala proti nižjemu... tako nekako kot na klancu sila na telo deluje v smeri od višje potencialne energije (=višine) k nižji. Če je torej gradient pozitiven, kar pomeni, da potencial v smeri gradienta narašča, je el. polje obrnjeno v nasprotno smer.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | MagnetizemOddelek: Šola | 1071 (802) | KOR111 |
| » | Razlika med linearnim elementom in nelinearnim (strani: 1 2 )Oddelek: Elektrotehnika in elektronika | 7216 (6327) | ZaphodBB |
| » | indukcijaOddelek: Šola | 1344 (1173) | rezator |
| » | El. nihajni krogOddelek: Elektrotehnika in elektronika | 2610 (2176) | Brane2 |
| » | Fizika - elektricno poljeOddelek: Šola | 2214 (1988) | ghostkop |