Forum » Šola » Surjektivno in Injektivni grafi
Surjektivno in Injektivni grafi
Cizimizi ::
Imam težave pri razumevanju ali je funkcija surjektivna ali injektivna, v srednji šoli.
Bolj me zaima prepoznavanje grafov in pod katero vrsto spadajo, brez katerega koli zapisa funkcije.
Primer:
Ne razumem zakaj je 1. graf surjektiven, 2. pa ne
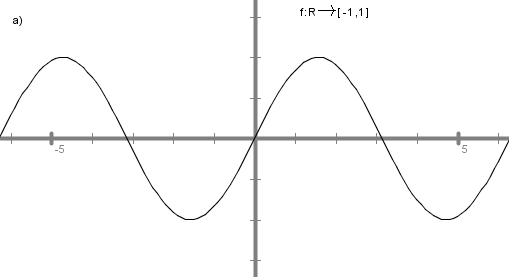
1. graf:
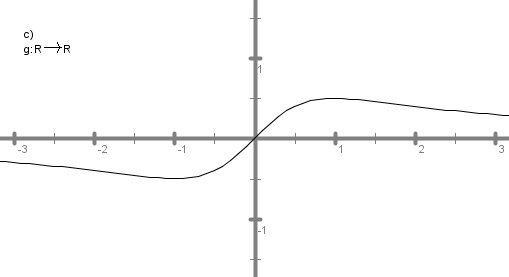
2. graf:
Kakor sem razumel Surjektivnost pomeni da mora osebovati vsa realna števila na y osi:
Zf = R
Ali to ne pomini da oba ne bi smela biti surjektivna?
Bolj me zaima prepoznavanje grafov in pod katero vrsto spadajo, brez katerega koli zapisa funkcije.
Primer:
Ne razumem zakaj je 1. graf surjektiven, 2. pa ne
1. graf:
2. graf:
Kakor sem razumel Surjektivnost pomeni da mora osebovati vsa realna števila na y osi:
Zf = R
Ali to ne pomini da oba ne bi smela biti surjektivna?
- spremenil: Cizimizi ()
Math Freak ::
Poglej si predpis funkcije:
prva: f: R -> [-1,1], vse vrednosti so dosežene od vključno -1 do vključno 1.
druga: g: R -> R, dosežene so samo vrednosti od približno -1/2 do 1/2. Torej še zdaleč ne celotna množica R.
Torej moraš gledati intervala [-1,1] za prvo in R za drugo.
Vsa realna števila na y osi mora vsebovati samo, če je funkcija oblike f: a -> R
prva: f: R -> [-1,1], vse vrednosti so dosežene od vključno -1 do vključno 1.
druga: g: R -> R, dosežene so samo vrednosti od približno -1/2 do 1/2. Torej še zdaleč ne celotna množica R.
Torej moraš gledati intervala [-1,1] za prvo in R za drugo.
Vsa realna števila na y osi mora vsebovati samo, če je funkcija oblike f: a -> R
Zgodovina sprememb…
- spremenilo: Math Freak ()
Cizimizi ::
Po pravici povedano, ne vem kaj točno pomeni ta puščica pri R -> [-1,1]
Mogoče če bom vedel, mi bo razlaga bolj jasna.
Mogoče če bom vedel, mi bo razlaga bolj jasna.
Math Freak ::
To je predpis funkcije: ta slika iz realnih števil v območje [-1,1].
Čeprav je ta prva slika čudno narisana. Ne vidim, kje ma enote na y osi ...
Čeprav je ta prva slika čudno narisana. Ne vidim, kje ma enote na y osi ...
Cizimizi ::
Okey torej druga slika dosega samo od -1/2 do 1/2. Ne razumem zakaj to ni "celotna" množica R. Od -1 do 1 pa je.
Zakaj je "celotna" množica R pomembna?
Ali niso realna števila preprosto vsa možna števila, ki obstajajo (razen imaginarna), vključno z 1/2 in -1/2
Zakaj je "celotna" množica R pomembna?
Ali niso realna števila preprosto vsa možna števila, ki obstajajo (razen imaginarna), vključno z 1/2 in -1/2
Zgodovina sprememb…
- spremenil: Cizimizi ()
Math Freak ::
Ti moraš gledati predpis množice:
Če bi imel recimo pri drugem primeru:
f: R->[-1/2,1/2] potem bi bila ta funkcija surjektivna, zato ker nas zanima samo interval [-1/2, 1/2] na y osi?
Če bi imel recimo pri drugem primeru:
f: R->[-1/2,1/2] potem bi bila ta funkcija surjektivna, zato ker nas zanima samo interval [-1/2, 1/2] na y osi?
Zgodovina sprememb…
- spremenilo: Math Freak ()
Math Freak ::
Za surjektivnost moraš ti gledati samo tisti interval na y osi, na katerem je funkcija predpisana.
f: R->[-1/2,1/2] je predpisana samo za y od -1/2 do 1/2, zato gledaš, če zavzame y vse vrednosti znotraj tega intervala vsaj enkrat.
f: R-> R je predpisana za y od -neskončno do +neskončno, zato gledaš, če zavzame y vse možne vrednosti znotraj realnih števil vsaj enkrat.
Drugače ti ne znam razložit =p.
f: R->[-1/2,1/2] je predpisana samo za y od -1/2 do 1/2, zato gledaš, če zavzame y vse vrednosti znotraj tega intervala vsaj enkrat.
f: R-> R je predpisana za y od -neskončno do +neskončno, zato gledaš, če zavzame y vse možne vrednosti znotraj realnih števil vsaj enkrat.
Drugače ti ne znam razložit =p.
Cizimizi ::
AJAAAA ok mislim da kapiram.
Sploh nisem vedel da zapis f: R-> vpliva na definicijo ali je surjektivna ali injektivna.
Torej če bi na prvem grafu pisalo f: R -> R potem tudi ta ne bi bil surjektiven?
Samo tega stavka še ne razumem
od kje je "a" prišel, oziroma kaj pomeni?
Sploh nisem vedel da zapis f: R-> vpliva na definicijo ali je surjektivna ali injektivna.
Torej če bi na prvem grafu pisalo f: R -> R potem tudi ta ne bi bil surjektiven?
Samo tega stavka še ne razumem
Vsa realna števila na y osi mora vsebovati samo, če je funkcija oblike f: a -> R
od kje je "a" prišel, oziroma kaj pomeni?
Zgodovina sprememb…
- spremenil: Cizimizi ()
Math Freak ::
ja, zapis zelo vpliva na surjektivnost =).
a je pač poljuben interval.
po navadi je funkcija zapisana kot:
f : A → B
in če je Zf = B, potem je funkcija surjektivna.
če je: R(realna števila)
f: A → R
in če je Zf = R, potem je funkcija surjektivna.
a je pač poljuben interval.
po navadi je funkcija zapisana kot:
f : A → B
in če je Zf = B, potem je funkcija surjektivna.
če je: R(realna števila)
f: A → R
in če je Zf = R, potem je funkcija surjektivna.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | OdvodiOddelek: Šola | 1805 (1200) | Math Freak |
| » | Surjektivno + Injektivno = Bijektivno ... huh!?Oddelek: Šola | 13975 (8726) | Math Freak |
| » | Mi lahko kdo razlozi ta graf?Oddelek: Šola | 3089 (1668) | BorutK-73 |
| » | zaporedjaOddelek: Šola | 2115 (1840) | technolog |
| » | Matematika - pomoč (strani: 1 2 3 )Oddelek: Šola | 30025 (26600) | daisy22 |