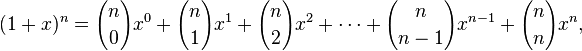Forum » Šola » Matematična indukcija!?!
Matematična indukcija!?!
alro ::
Dokaži neenakost:
(1+x)^n >= 1 + nx
za vsak n (pripada) N.
A bi mogoče kdo zanu mi to pokazat kako rešt. Bi biu res hvaležn.
Hvala.
(1+x)^n >= 1 + nx
za vsak n (pripada) N.
A bi mogoče kdo zanu mi to pokazat kako rešt. Bi biu res hvaležn.
Hvala.
čuhalev ::
Namig: desna stran sta le prva dva člena binomske vrste.
In gre tudi brez, v eni vrstici.
In gre tudi brez, v eni vrstici.
Zgodovina sprememb…
- spremenil: čuhalev ()
alro ::
JA jest sm zdej šou tko k so nam pokazal sam nevem pol ne znam naprej kaj treba narest
(1+x)(1+x)^n >= 1+(n+1)x
in pol naprej sploh nevem kaj je naredu profesor
To k je na n pa sploh nevem kako razstavt
(1+x)(1+x)^n >= 1+(n+1)x
in pol naprej sploh nevem kaj je naredu profesor
To k je na n pa sploh nevem kako razstavt
lebdim ::
tisto na n naj te ne zavede, saj gre za splošno formulo dvočlenika (binoma) na n-to potenco ...
kar moraš dokazat pri trditvi za N+1, da je (1+x)(N+1) > = 1 + (N+1)x
ob predpostavki, da je (1 + x)N > = 1 + Nx
kar moraš dokazat pri trditvi za N+1, da je (1+x)(N+1) > = 1 + (N+1)x
ob predpostavki, da je (1 + x)N > = 1 + Nx
Rokm ::
lebdim ::
saj piše v navodilu, da za vsak n, ki pripada naravnim številom ... torej, to pomeni, npr. za n = 3,
da je (x + 1)3 > = 1 + 3x
da je (x + 1)3 > = 1 + 3x
Zgodovina sprememb…
- spremenil: lebdim ()
lebdim ::
@Rokm, haha, ja pa res ...
@alro, daj napiši celotno navodilo naloge, kaj je treba naredit oz. dokazat ...
@alro, daj napiši celotno navodilo naloge, kaj je treba naredit oz. dokazat ...
lebdim ::
aha, dobro ... @Rokm: potem pa ta "x" ne igra nobene vloge ...
@alro:
tako kot sem ti že zgoraj napisal: npr. trditev za n = 3: (1 + x)3 >= 1 + 3x, kar je res.
npr. (1+x)3 = 1 + 3x + 3x2 + x3, in to je definitivno večje ali enako 1 + 3x.
ampak to je bil zgolj primer za n = 3. tebe pa naloga sprašuje za vsako naravno število.
pomagaj si z zgornjimi mojimi "namigi" oz. razmišljanji.
najprej si izberi bazo indukcijo, npr. n = 1 ali n = 2, in preveri trditev, ki jo dokazuješ, torej to neenačbo (vstavi vrednosti).
potem pa narediš indukcijski korak. pri tem pa moraš dokazati trditev T(n+1), torej namesto n vstaviš N+1 (v to neenačbo).
@alro:
tako kot sem ti že zgoraj napisal: npr. trditev za n = 3: (1 + x)3 >= 1 + 3x, kar je res.
npr. (1+x)3 = 1 + 3x + 3x2 + x3, in to je definitivno večje ali enako 1 + 3x.
ampak to je bil zgolj primer za n = 3. tebe pa naloga sprašuje za vsako naravno število.
pomagaj si z zgornjimi mojimi "namigi" oz. razmišljanji.
najprej si izberi bazo indukcijo, npr. n = 1 ali n = 2, in preveri trditev, ki jo dokazuješ, torej to neenačbo (vstavi vrednosti).
potem pa narediš indukcijski korak. pri tem pa moraš dokazati trditev T(n+1), torej namesto n vstaviš N+1 (v to neenačbo).
Zgodovina sprememb…
- spremenil: lebdim ()
MaFijec ::
A bi lahko prosim nehali podpirati lenobo.
Kar zmrazi me, ko vidim, koliko tem je tukaj samo zato, ker nekateri niso pripravljeni vložiti niti najmanjšega truda.
Če jim pomagate, se ne bodo nikoli naučili (razumeli!) nič.
Rešitev naloge je direkta uporaba indukcije, seveda če si prej kdaj prebereš, kaj naj bi indukcija bila in to razumeš.
Baza indukcije?
Korak indukcije, n->n+1?
Seveda je prej treba vedeti, kaj je potenciranje, to pa zgleda ni več samoumevno.
Kar zmrazi me, ko vidim, koliko tem je tukaj samo zato, ker nekateri niso pripravljeni vložiti niti najmanjšega truda.
Če jim pomagate, se ne bodo nikoli naučili (razumeli!) nič.
Rešitev naloge je direkta uporaba indukcije, seveda če si prej kdaj prebereš, kaj naj bi indukcija bila in to razumeš.
Baza indukcije?
Korak indukcije, n->n+1?
Seveda je prej treba vedeti, kaj je potenciranje, to pa zgleda ni več samoumevno.
alro ::
Spet sem se zmedel, imam primer 2n >= (n+1);
In najprej za n vsavim notri 0 in dobim 20 >= (0+1) ---> 1 >= 1 ?
Potem pa za n vstavim (n+1) in dobim 2(n+1) >= ((n+1)+1); ?
Sedaj pa tukaj naprej nevem kaj naj naredim in kako vem kdaj nehati razstavljati?
Hvala in lep pozdrav
In najprej za n vsavim notri 0 in dobim 20 >= (0+1) ---> 1 >= 1 ?
Potem pa za n vstavim (n+1) in dobim 2(n+1) >= ((n+1)+1); ?
Sedaj pa tukaj naprej nevem kaj naj naredim in kako vem kdaj nehati razstavljati?
Hvala in lep pozdrav
čuhalev ::
Baza indukcije ...
1 >= 1 ?
Nisi prepričan, če je to res? Je res. Imaš dokazano za n=0. Pri večini nalog z indukcijo je to najlažji korak.
Indukcijski korak ...
namig: Nekje moraš obvezno uporabiti indukcijsko predpostavko 2n >= (n+1) oziroma s tem pokazati, da velja 2(n+1) >= ((n+1)+1);
1 >= 1 ?
Nisi prepričan, če je to res? Je res. Imaš dokazano za n=0. Pri večini nalog z indukcijo je to najlažji korak.
Indukcijski korak ...
namig: Nekje moraš obvezno uporabiti indukcijsko predpostavko 2n >= (n+1) oziroma s tem pokazati, da velja 2(n+1) >= ((n+1)+1);
alro ::
Saj to me zanima kako od tam naprej, ker ko v šoli to gledam iz tega 2(n+1) >= ((n+1)+1) nastane nekaj čisto drugega in nevem kako je do tega prišlo...
čuhalev ::
Pa ne smeš iz tega izhajati, to moraš dobiti na koncu.
Začneš z 2n >= (n+1) in napleteš to, kar si napisal.
Mimogrede ta naloga je popolnoma enaka tisti prej (1 + x)^n > = 1 + nx, le da za x postaviš x=1.
Začneš z 2n >= (n+1) in napleteš to, kar si napisal.
Mimogrede ta naloga je popolnoma enaka tisti prej (1 + x)^n > = 1 + nx, le da za x postaviš x=1.
Zgodovina sprememb…
- spremenil: čuhalev ()
simpatija ::
Velikokrat z indukcijo narediš tako, da ugotoviš, kaj moraš narest tisti enačbi kjer je notr "n", da potem na eni strani dobiš tisto, kar rabiš v enačbi z "n+1" (al kej prišteješ, al s čem pomnožiš, ...). Glej spodaj. Potem pa še drugo stran računaš, pa mal oblikuješ tako, da dobiš tisto kar rabiš.
So pa še drugi načini kako dokazat z indukcijo stvari.
Rabiš dobit 2(n+1) >= ((n+1)+1).
Imaš pa 2n >= (n+1).
Zdej pa razmišljaš, ok mam 2n, kako iz tega dobim 2(n+1) ? Takole: 2(n+1) = 2n * 2.
Aha, fino. Ampak ker mam enačbo, ne smem kar takole množit samo 2n, ampak moram na obeh straneh pomnožit. Se pravi imam zdaj: 2n *2 >= (n+1)*2.
Aha kul, tole že zgleda zelo podobno tistemu, kar rabim dobit. Zdej pa vse skup mal preoblikuješ, tko da zgleda čimbl podobno tistemu, kar moraš dobit:
2(n+1) >= 2n + 2
2(n+1) >= n + n + 1 +1
2(n+1) >= ((n + 1) +1) + n
Aha, to kar je zdaj na desni, se pravi ((n + 1) +1) + n, je pa zihr večje od (n+1)+1
Se pravi 2(n+1) >= ((n + 1) +1) + n >= (n+1)+1.
Se pravi je 2(n+1) >= (n+1)+1.
So pa še drugi načini kako dokazat z indukcijo stvari.
Rabiš dobit 2(n+1) >= ((n+1)+1).
Imaš pa 2n >= (n+1).
Zdej pa razmišljaš, ok mam 2n, kako iz tega dobim 2(n+1) ? Takole: 2(n+1) = 2n * 2.
Aha, fino. Ampak ker mam enačbo, ne smem kar takole množit samo 2n, ampak moram na obeh straneh pomnožit. Se pravi imam zdaj: 2n *2 >= (n+1)*2.
Aha kul, tole že zgleda zelo podobno tistemu, kar rabim dobit. Zdej pa vse skup mal preoblikuješ, tko da zgleda čimbl podobno tistemu, kar moraš dobit:
2(n+1) >= 2n + 2
2(n+1) >= n + n + 1 +1
2(n+1) >= ((n + 1) +1) + n
Aha, to kar je zdaj na desni, se pravi ((n + 1) +1) + n, je pa zihr večje od (n+1)+1
Se pravi 2(n+1) >= ((n + 1) +1) + n >= (n+1)+1.
Se pravi je 2(n+1) >= (n+1)+1.
lebdim ::
jaz bi dodal samo še teoritično opazko.
in sicer, da ponavadi tisto trditev, ki jo dokazuješ, da velja za vsako naravno število n, označiš s T(n). Potem pa, ko dokazuješ trditev za n+1, to trditev označiš s T(n+1). Ker je princip indukcije ravno v tem, da dokažeš veljavnost trditve T(n+1) in potem sklepaš takole: Ker velja trditev T(n+1) za vsako naravno število, potem velja tudi T(n) za vsako število.
in sicer, da ponavadi tisto trditev, ki jo dokazuješ, da velja za vsako naravno število n, označiš s T(n). Potem pa, ko dokazuješ trditev za n+1, to trditev označiš s T(n+1). Ker je princip indukcije ravno v tem, da dokažeš veljavnost trditve T(n+1) in potem sklepaš takole: Ker velja trditev T(n+1) za vsako naravno število, potem velja tudi T(n) za vsako število.
upam, da nisem pretirano zakompliciral, saj sem hotel povedati le to, da moraš v bistvu pokazati trditev T(n+1).
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | matematika - pomočOddelek: Šola | 4274 (3329) | lebdim |
| » | IndukcijaOddelek: Šola | 1203 (955) | lebdim |
| » | Matematika: Deljivost naravnih in celih števil.Oddelek: Šola | 3769 (3571) | lebdim |
| » | matematična indukcija + inverz f(x) (pomoč)Oddelek: Šola | 1428 (1384) | minusnič |
| » | matematkaOddelek: Šola | 3470 (2449) | lebdim |