Forum » Loža » dvojni integral, pomoc
dvojni integral, pomoc
Yosh ::
Imam eno nalogo, pa nevem kako bi jo resil, bi prosil nekoga, ce bi bil voljen mi pomagat( namignit)
Naloga se glasi takole :
Izracunaj ploscino lika,omejenga s krivuljami y^2 = 4ax, x+y = 3a, in y= 0, s pomočjo dvojnega integrala.
Hvala, lp
Naloga se glasi takole :
Izracunaj ploscino lika,omejenga s krivuljami y^2 = 4ax, x+y = 3a, in y= 0, s pomočjo dvojnega integrala.
Hvala, lp
Share with others, your inner joy, goodness and beauty , and dont hurt them.
ta-mau ::
tam je blo najbrž mišljeno y>=0...
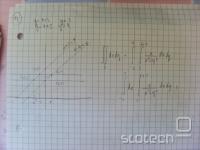
poskušaj tko da si najprej probaš na grobo skicirat krivulji in videt katero površino zajemata. v tvojem primeru imaš parabolo zarotirano za -90 (y=sqrt(4ax)) in pa linearno premico ki seka x pri 3a. Iz skice boš najbrž vidu da se krivulje v določeni točki lomita. tako da boš integriral dvakrat. Prvi dvojni integral ima meje po x€{0,presečišče}, y€{0,sqrt(4ax)} drugi kos pa x€{presečišče,3a}, y€{0,3a-x}.
poskušaj tko da si najprej probaš na grobo skicirat krivulji in videt katero površino zajemata. v tvojem primeru imaš parabolo zarotirano za -90 (y=sqrt(4ax)) in pa linearno premico ki seka x pri 3a. Iz skice boš najbrž vidu da se krivulje v določeni točki lomita. tako da boš integriral dvakrat. Prvi dvojni integral ima meje po x€{0,presečišče}, y€{0,sqrt(4ax)} drugi kos pa x€{presečišče,3a}, y€{0,3a-x}.
Yosh ::
hm, a lahko naredim tako da graf zarotiram, naredim da je x funkcija y, in potem poracunam presecisca.. recem da je a = 1.. dobim dve ničli za x = 1, in x= 9, vstavim v enacbo x = y^2/4 dobim ven y = 2 in za drugo ničlo k je x = 9, dobim y= 6.
POtem pa integriram( en integral) od 2max do 6 min ( gledam po y osi) izraz (y^4 - 12a -4y/4 )dy ...
a je to prav?
POtem pa integriram( en integral) od 2max do 6 min ( gledam po y osi) izraz (y^4 - 12a -4y/4 )dy ...
a je to prav?
Share with others, your inner joy, goodness and beauty , and dont hurt them.
Yosh ::
aha. Hvala.
Samo zanima me presečišče pri drugem integralu ko je xEUR( presečišče, 3a), katero je to presečišče?
xEUR{0,presečišče}, yEUR{0,sqrt(4ax)} drugi kos pa xEUR{presečišče,3a}, yEUR{0,3a-x}.
torej pri prvem xEUR{0,3a-y} , drugi kos pa xEUR{presečišče, 3a} ?
Samo zanima me presečišče pri drugem integralu ko je xEUR( presečišče, 3a), katero je to presečišče?
xEUR{0,presečišče}, yEUR{0,sqrt(4ax)} drugi kos pa xEUR{presečišče,3a}, yEUR{0,3a-x}.
torej pri prvem xEUR{0,3a-y} , drugi kos pa xEUR{presečišče, 3a} ?
Share with others, your inner joy, goodness and beauty , and dont hurt them.
ta-mau ::
'a' ne smeš kar definirat in izbrat da je npr 1, lahko pa to narediš na koncu če želiš preverit ali si prav izračunal integral. Naloga te sprašuje za ploščino tega lika če je 'a' neznan. Torej zanima te kakšne vrednosti ploščin boš dobil če se bo a spreminjal, kar pomeni da bo rezultat dvojnega integrala odvisen od spremenljivke 'a'.
Za presečišča si poskusi pomagat z enačbo x_1,_2=\frac{-b\pm\sqrt{b^2-4ac}}{2a} (napaka se odpravlja), kjer dobiš 2 možni rešitvi (krivulji se sekata v dveh presečiščih) . vzemi tisto pri kateri se krivulji sekata v prvem kvadrantu. ko maš presečišče določeno lahko računaš integrala z mejami podanimi v prvem postu..
Za preiskus pravilnosti izračuna integrala lahko poskusiš vzet a=1 ter ga vstaviš v izračunan integral, po drugi strani pa a vstaviš v enačbo kjer si imel a še nedefiniran.. rezultata se morata ujemati za poljuben a, ki je večji od 0 (to sledi iz enačbe y^2...).
Za presečišča si poskusi pomagat z enačbo x_1,_2=\frac{-b\pm\sqrt{b^2-4ac}}{2a} (napaka se odpravlja), kjer dobiš 2 možni rešitvi (krivulji se sekata v dveh presečiščih) . vzemi tisto pri kateri se krivulji sekata v prvem kvadrantu. ko maš presečišče določeno lahko računaš integrala z mejami podanimi v prvem postu..
Za preiskus pravilnosti izračuna integrala lahko poskusiš vzet a=1 ter ga vstaviš v izračunan integral, po drugi strani pa a vstaviš v enačbo kjer si imel a še nedefiniran.. rezultata se morata ujemati za poljuben a, ki je večji od 0 (to sledi iz enačbe y^2...).
Yosh ::
Imam pa se eno vprasanje.. te meje me ubijajo.. ni mi cisto jasno potek y in x.. na grafu.. torej pri fiksnem x( sprememba y) in pri pri fiksnem y ( sprememba x)..
naloga pa se glasi takole.
y= x+3
y=x+5
y= 4, y= 3
integriram pa x/(x^2 +y^2)
naloga pa se glasi takole.
y= x+3
y=x+5
y= 4, y= 3
integriram pa x/(x^2 +y^2)
Share with others, your inner joy, goodness and beauty , and dont hurt them.
Zgodovina sprememb…
- zavarovalo slike: WarpedGone ()
JCD ::
Tako kot bi rad integriral, je najbolje da razdeliš zadevo na tri integrale.
Prvega
\int_{-2}^{-1}dx\int_3^{x+5}\frac{x}{x^2 y^2}dy (napaka se odpravlja),
drugega
\int_{-1}^{0}dx\int_3^{4}\frac{x}{x^2 y^2}dy (napaka se odpravlja)
in tretjega
\int_{0}^{1}dx\int_{x 3}^{4}\frac{x}{x^2 y^2}dy (napaka se odpravlja)
Pač najprej pogledaš kje teče x, nato pa fiksiraš en x in pogledaš kako po tistem fiksiranem x-u teče y-lon. Lahko pa najprej integriraš po y-lonu in nato po x-u. Takrat boš imel samo en integral za rešit.
Prvega
\int_{-2}^{-1}dx\int_3^{x+5}\frac{x}{x^2 y^2}dy (napaka se odpravlja),
drugega
\int_{-1}^{0}dx\int_3^{4}\frac{x}{x^2 y^2}dy (napaka se odpravlja)
in tretjega
\int_{0}^{1}dx\int_{x 3}^{4}\frac{x}{x^2 y^2}dy (napaka se odpravlja)
Pač najprej pogledaš kje teče x, nato pa fiksiraš en x in pogledaš kako po tistem fiksiranem x-u teče y-lon. Lahko pa najprej integriraš po y-lonu in nato po x-u. Takrat boš imel samo en integral za rešit.
Ktj ::
Zakaj bi razbijal na tri podintegrale ko se pa da z enim samim izračunat.
Namig: zamenjaj vrstni red integreranja!
Namig: zamenjaj vrstni red integreranja!
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | MatematikaOddelek: Šola | 3834 (2614) | Math Freak |
| » | naslednji dve nalogi iz Matematike 2Oddelek: Šola | 2671 (2221) | lebdim |
| » | Matematika - pomoč (strani: 1 2 3 )Oddelek: Šola | 29885 (26460) | daisy22 |
| » | Dvojni integral, pomočOddelek: Šola | 4952 (4527) | Yosh |
| » | Pomoč pri nalogi.Oddelek: Šola | 1920 (1626) | Jean-Paul |