Forum » Znanost in tehnologija » Neural Networks
Neural Networks
gzibret ::
Neural Network - a tutorial
Že dolgo sem pri sebi premleval o tem, da bi napisal tole zadevo, ampak sem šele sedaj našel nekaj časa. Ta tema je namenjena debatiranju o tej veji umetne inteligence in osnovni seznanitvi o tem, kaj umetne nevronske mreže sploh so in za kaj se uporabljajo. Če koga zanima kaj več, naj napiše ZS ali pa vpraša tukaj. Konstruktivne dopolnitve tutoriala zelo zaželjene. Zadeva je zanalašč napisana bolj "kunštno" v veselje vsem nadobudnim prepisovalcem seminarskih nalog.
No, pa začnimo:
Nevronske mreže se danes uspešno uporabljajo na številnih področjih - finančništvo, medicina, tehnika, geologija, biologija, fizika, elektrotehnika, robotika... Uspeh metode je pripisati sledečim faktorjem:
- zmožne so modelirati ekstremno kompleksne sisteme; lahko se uporabijo tam, kjer lineranost* (običajna statistika npr.) odpove;
- ni težav z dimenzionalnostjo problema - le ta je lahko poljubna;
- lahke za uporabo; metode strojnega učenja nam omogočajo uporabo nevronskih mrež kot uporabo črne ali pa sive škatle.
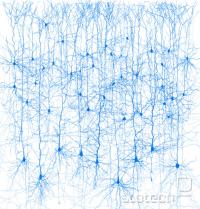
Metoda temelji na posnemanju biološkega živčevja. V nevron (živčno celico) prihajajo vhodni signali. Če je vsota vhodov dovolj velika, nevron proža signale naprej v nove nevrone, ali pa v motorične celice (mišice npr.). Dovolj velika mreža teh enostavnih enot (slika 1) lahko ima neslutene procesorske zmožnosti, vključno z razumenavnjem tega, kar sedajle berete.
Slika 1. Vir: IBM blue brain project.
Prvi matematični opis sta naredila biologa McCullogh & Pitts leta 1943. Ta opis temelji na sledečih aksiomih, ki sta jih ugotovila na podlagi opazovanj posameznih živčnih celic:
1) aktivacija nevrona temelji na pravilu vse-ali-nič; nevron je ali aktiviran ali ni aktiviran, vmesna stanja ne obstajajo;
2) določeno število sinaps lahko vzburi nevron v določenem časovnem obdobju, če je vsota vhodnih dražljajev večja od nadpražnega dražljaja;
3) edina pomembna zakasnitev pri prenosu signalov je v sinapsah;
4) aktivnost v inhibitorskih sinapsah preprečuje aktivacijo nevrona v nekem časovnem obdobju;
5) struktura povezav v mreži nevronov je v času konstantna
Matematično zadeva izgleda takole (slika 2), poimenujemo pa jo lahko na več načinov: binarni model nevrona, linearni model...:
Slika 2.
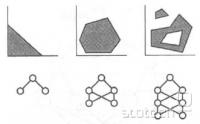
Če opisane osnovne gradnike povežemo v mrežo, že lahko govorimo o umetni nevronski mreži. Zgolj z uporabo mreže McCullogh-Pittsovih nevronov lahko zgradimo stroj, ki je ekvivalent touringovemu stroju oz. VLSI sistemom (very large scale integration oz. slovensko integrirana vezja). V žargonu: zmore vse, kar zmore računalnik, saj lahko s temi nevroni simuliramo vse logične operacije: NOT, OR, AND, XOR (slika 3)... Obstaja več imen za takšne mreže, omenil pa bom dve: perceptron in pa "adaline".
Slika 3. AND, OR, NOT in XOR logična vrata z uporabo nevronov.
Izboljšan model umetnega nevrona je imenovan kot nelinearni model. Izbrisan je peti McCullogh-pittsov aksiom, dodana korekcija (bias) in aktivacijska funkcija, ki vsoto vhodnih signalov (seveda upoštevajoč tudi bias) pretvori v izhod. Na spodnji sliki (slika 4) je model nelinearnega nevrona skupaj z aktivacijsko funkcijo. Le-ta je sigmoidalna funkcija, ki se pri nevronskih mrežah največ uporablja ( sig(x)=1/(1-e^(-a*x)) ). Vendar moramo paziti to, da morajo pri sigmoidalni funkciji vsi podatki biti na intervalu med [0,1] ali še bolje, med [0.05,0.95]. Če imamo podatke na intervalu med [-1,+1], pa lahko uporabimo npr. tangens hiperbolicus funkcijo, ali pa katero drugo, npr. "piecewise linear function".
Slika 4.
Še en model nevrona naj omenim, to je nevron s krožno aktivacijsko funkcijo (radial activation function). Njegovo delovanje je rahlo drugačno, saj vhode obravnava kot vektor v prostoru. Izhod tega nevrona pa se izračuna na podlagi razdalje med vhodnim vektorjem in tarčnim vektorjem, ki je "shranjen" v nevronu. Razdalja je lahko evklidska ali pa katera neevklidska. Aktivacijska funkcija na koncu pretvori razdaljo v aktivacijo na način, da bližje je vhodni vektor ciljnemu, višja je aktivacija. Mreže, ki vsebujejo radialne nevrone (slika 5), se imenujejo kot RBF mreže (radial basis function networks).
Slika 5.
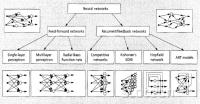
Če te osnovne gradnike povežemo v mrežo, dobimo nevronsko mrežo (slika 6). Le-te se delijo na dva osnovna tipa: na mreže brez povratnih zank in na mreže s povratnimi zankami. Pri prvih teče signal vedno od vhodnih nevronov proti izhodnim. Vsak vhodni podatek se obravnava kot ločena entiteta. Predhodni podatki na delovanje mreže nimajo vpliva. Drugi tip mrež pa vsebuje t.i. povratne povezave. Pri njih je delovanje odvisno od zaporedja vhodnih signalov oz. od predhodnih vhodnih podatkov. Detajlneje mrež ne bom opisoval, če koga zanima kaj več, naj poišče na guglu (ključne besede pa so napisane na sliki).
Slika 6. Vir: Jain et al., 1996: Artificial neural networks: A tutorial. IEEE.
Preden nevronsko mrežo uporabimo, jo moramo naučiti. Učni proces priredi obtežbe mednevronskih povezav in pa biase tako, da je delovanje mreže ustrezno za rešitev naše naloge. Poznamo tri osnovne principe učenja. Pri prvem tipu učenja - nadzorovanem (supervised) učenju - se povezave urejujejo na podlagi učnih podatkov, ki vsebujejo znane vhodne in pripadajoče izhodne vrednosti. Pred začetkom učenja se vsi prosti parametri mreže (uteži, biasi) postavijo na naključne vrednosti. Algoritem za učenje (najbolj znan je t.i. backpropagation learning algorythm) pa te vrednosti počasi, korak za korakom, prireja tako, da napaka med izračunanimi in pričakovanimi izhodnimi vrednostmi pada proti ničli.
Drugi tip učenja je nenadzorovano učenje (unsupervised), kjer učni algoritem prireja proste parametre mreže zgolj na podlagi vhodnih vrednosti. Osnova tem učnim algoritmom je "tekmovanje za prevlado". Zmagovalni nevron se ojača, drugi nevroni se oslabijo. Na takšen način na koncu dobimo vhodne podatke klasificirane v različne razrede.
Tretji tip učenja je ojačitveno (reinforced) učenje. To je posebna vrsta nadzorovanega učenja, uporabljena predvsem pri učenju časovnih vrst, kjer rezultata neke akcije ne izvemo takoj, ampak šele čez nekaj časa. Primer je igranje šaha. Ali je bila naša strategija uspešna ali ne, ponavadi izvemo šele po nekaj potezah.
Omenil bi še evolucijsko učenje, ki deluje na podoben način, kot evolucijski algoritmi (naključne mutacije, preizkus delovanja, rekombinacija najboljših...).
Zakaj so nevronske mreže uporabne? Nevronske mreže so znane kot univerzalni aproksimatorji, saj lahko aproksimirajo poljubno zvezno funkcijo poljubno natančno, če le imamo dovolj učnih podatkov in dovolj kompleksno mrežo. Pri tem ni omejitev glede števila vhodnih in izhodnih spremenljivk oz. z drugimi besedami, ni omejitve glede dimenzionalnosti prostorov, kjer poteka preslikava. Zaradi dodelanih algoritmov strojnega učenja in hitrih procesorjev so izjemno lahke in priročne za uporabo. Nevronske mreže prebavijo skoraj vse: uporabljeni podatki so lahko pomanjkljivi, podvrženi šumu, napakam, lahko so atrubutivne narave (npr. slab-srednje-dober; grudast-mrvičast-oreškast-poliedričen), ne potrebujemo normalne porazdelitve... Lahko klasificirajo podatke takrat, ko običajna statistika odpove (slika 7). Povratne povezave omogočajo simulacijo zelo kompleksnih dinamičnih sistemov ali pa napovedovanje časovnih vrst (napovedovanje gibanja cen delnic so sanje vsakega ekonomista, samo pazi; nobena izmed firm, ki prodaja programske simulatorje nevronskih mrež za prav ta namen, se ne ukvarja z delnicami). Zmožne so prepoznave črk, slik, govora (pattern recognition). Uporabne so za kontrolo proizvodnih procesov, strojev, robotov, za optimizacijo procesov...
Slika 7.
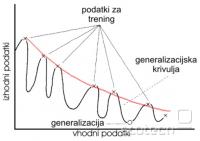
Težave pri uporabi nevronskih mrež pa so sledeče: podatke moramo normalizirati na interval med 0 in 1 ali pa med -1 in +1. Obstaja večna dilema, kako kompleksna mreža je ravno primerno kompleksna za naš problem. Če uporabimo premalo kompleksno mrežo, problema ne bo mogla rešiti, preveč kompleksna mreža pa se je zmožna učne primere "napiflati" in nima sposobnosti t.i. generalizacije (slika 8) oz. pravilne rešitve primerov, pri katerih mreže nismo učili. Pri učenju mreže nikoli ne vemo, ali smo mrežo naučili dovolj, premalo ali pa morda celo preveč. Na sliki 9 nam krivulja 2 predstavlja padanje napake učnih podatkov, če povečujemo število učnih ciklov, krivulja 2 pa napako, ki jo naredi mreža pri podatkih, katerih nismo uporabili za učenje. Otimalno število učnih ciklov je označeno s krogcem. Povečevanje učnih ciklov vodi v "overfitting", čeprav nam učna napaka še vedno pada. torej smo dosegli popolnoma napačno generalizacijo in tega nam učna napaka sploh ne pokaže.
Slika 8. Vir: Haykin, 1999.
Slika 9. Vir: Kasabov, 1998. Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering. The MIT Press.
Nikoli tudi ne vemo, ali smo dosegli minimalno možno napako. Učenje se nam lahko ustavi na katerem od "lokalnih" minimumov (točka 1 na sliki 10), namesto na globalnem minimumu (točka 2 na sliki 10). Še huje, mreža se nam sploh noče učiti.....
Slika 10. Vir: Boddy & Morris, 1999. Artificial neural networks for pattern recognition. In.: Machine learning methods for ecological applications. Kluwer.
Za konec pa je treba vedeti predvsem to, da nevronske mreže niso nek vsevedni in vsemogočni pripomoček. V prvi vrsti jih omejujejo učni podatki. Saj veste: garbage in, garbage out. Lep primer opisuje zgodbica na tejle povezavi: Neil Fraser: Writing: Neural Network Follies. Prav tako ne morejo aproksimirati nečesa, kar sploh nima vzročne povezave, npr. na podlagi števila ptic selivk izračunati količino frizerskih storitev.
Za konec še nekaj slikic nevronskih mrež z opisi:
Slika 11: večslojni perceptron (Multilayer perceptron - MLP) s 36 vhodnimi nevroni, devetimi procesorskimi ali skritimi (hidden) nevroni in enim izhodnim nevronom (rezultat). Signal poteka od vrha slike proti dnu.
Slika 12: večslojni perceptron (MLP) z dvema procesorskima "skritima" slojema.
Slika 13: razlika med zmožnostjo ločevanja (klasifikacije) med perceptronom, MLP-jem z enim slojem skritih nevronov in MLP-jem z dvema slojema skritih nevronov. Vir: Bishop, 1995.
Slika 14: radial basis function networks oz. mreža z radialnimi nevroni (krogci). Te mreže vedno vsebujejo plast navadnih nelinearnih nevronov za plastjo radialnih nevronov.
Slika 15: samoorganizacijske mreže ali SOM mreže (self-organizing maps). Te mreže učino na podlagi nenadzorovanega učenja. Nevroni tekmujejo za prevlado. Znane so kot zelo zmogljivi klasifikatorji podatkov.
Literatura:
biblija: Bishop, 1995. Neural Networks for Pattern Recognition. Oxford University Press.
Matematika: Haykin, 1999. Neural Networks - a comprehensive foundation. Prentice Hall.
Dober FAQ: ftp://ftp.sas.com/pub/neural/FAQ.html
SLAIS: Slovensko društvo za umetno inteligenco
Free simulator: MemBrain
Free simulator v javi: JavaNNS
Najboljši vir: klik
* linearnost tukaj pomeni, da se jo da opisovati z metodami linearne algebre. Transformacija je torej aditivna in homogena. Več o tem tukaj: klik
Že dolgo sem pri sebi premleval o tem, da bi napisal tole zadevo, ampak sem šele sedaj našel nekaj časa. Ta tema je namenjena debatiranju o tej veji umetne inteligence in osnovni seznanitvi o tem, kaj umetne nevronske mreže sploh so in za kaj se uporabljajo. Če koga zanima kaj več, naj napiše ZS ali pa vpraša tukaj. Konstruktivne dopolnitve tutoriala zelo zaželjene. Zadeva je zanalašč napisana bolj "kunštno" v veselje vsem nadobudnim prepisovalcem seminarskih nalog.
No, pa začnimo:
Nevronske mreže se danes uspešno uporabljajo na številnih področjih - finančništvo, medicina, tehnika, geologija, biologija, fizika, elektrotehnika, robotika... Uspeh metode je pripisati sledečim faktorjem:
- zmožne so modelirati ekstremno kompleksne sisteme; lahko se uporabijo tam, kjer lineranost* (običajna statistika npr.) odpove;
- ni težav z dimenzionalnostjo problema - le ta je lahko poljubna;
- lahke za uporabo; metode strojnega učenja nam omogočajo uporabo nevronskih mrež kot uporabo črne ali pa sive škatle.
Metoda temelji na posnemanju biološkega živčevja. V nevron (živčno celico) prihajajo vhodni signali. Če je vsota vhodov dovolj velika, nevron proža signale naprej v nove nevrone, ali pa v motorične celice (mišice npr.). Dovolj velika mreža teh enostavnih enot (slika 1) lahko ima neslutene procesorske zmožnosti, vključno z razumenavnjem tega, kar sedajle berete.
Slika 1. Vir: IBM blue brain project.
Prvi matematični opis sta naredila biologa McCullogh & Pitts leta 1943. Ta opis temelji na sledečih aksiomih, ki sta jih ugotovila na podlagi opazovanj posameznih živčnih celic:
1) aktivacija nevrona temelji na pravilu vse-ali-nič; nevron je ali aktiviran ali ni aktiviran, vmesna stanja ne obstajajo;
2) določeno število sinaps lahko vzburi nevron v določenem časovnem obdobju, če je vsota vhodnih dražljajev večja od nadpražnega dražljaja;
3) edina pomembna zakasnitev pri prenosu signalov je v sinapsah;
4) aktivnost v inhibitorskih sinapsah preprečuje aktivacijo nevrona v nekem časovnem obdobju;
5) struktura povezav v mreži nevronov je v času konstantna
Matematično zadeva izgleda takole (slika 2), poimenujemo pa jo lahko na več načinov: binarni model nevrona, linearni model...:
Slika 2.
Če opisane osnovne gradnike povežemo v mrežo, že lahko govorimo o umetni nevronski mreži. Zgolj z uporabo mreže McCullogh-Pittsovih nevronov lahko zgradimo stroj, ki je ekvivalent touringovemu stroju oz. VLSI sistemom (very large scale integration oz. slovensko integrirana vezja). V žargonu: zmore vse, kar zmore računalnik, saj lahko s temi nevroni simuliramo vse logične operacije: NOT, OR, AND, XOR (slika 3)... Obstaja več imen za takšne mreže, omenil pa bom dve: perceptron in pa "adaline".
Slika 3. AND, OR, NOT in XOR logična vrata z uporabo nevronov.
Izboljšan model umetnega nevrona je imenovan kot nelinearni model. Izbrisan je peti McCullogh-pittsov aksiom, dodana korekcija (bias) in aktivacijska funkcija, ki vsoto vhodnih signalov (seveda upoštevajoč tudi bias) pretvori v izhod. Na spodnji sliki (slika 4) je model nelinearnega nevrona skupaj z aktivacijsko funkcijo. Le-ta je sigmoidalna funkcija, ki se pri nevronskih mrežah največ uporablja ( sig(x)=1/(1-e^(-a*x)) ). Vendar moramo paziti to, da morajo pri sigmoidalni funkciji vsi podatki biti na intervalu med [0,1] ali še bolje, med [0.05,0.95]. Če imamo podatke na intervalu med [-1,+1], pa lahko uporabimo npr. tangens hiperbolicus funkcijo, ali pa katero drugo, npr. "piecewise linear function".
Slika 4.
Še en model nevrona naj omenim, to je nevron s krožno aktivacijsko funkcijo (radial activation function). Njegovo delovanje je rahlo drugačno, saj vhode obravnava kot vektor v prostoru. Izhod tega nevrona pa se izračuna na podlagi razdalje med vhodnim vektorjem in tarčnim vektorjem, ki je "shranjen" v nevronu. Razdalja je lahko evklidska ali pa katera neevklidska. Aktivacijska funkcija na koncu pretvori razdaljo v aktivacijo na način, da bližje je vhodni vektor ciljnemu, višja je aktivacija. Mreže, ki vsebujejo radialne nevrone (slika 5), se imenujejo kot RBF mreže (radial basis function networks).
Slika 5.
Če te osnovne gradnike povežemo v mrežo, dobimo nevronsko mrežo (slika 6). Le-te se delijo na dva osnovna tipa: na mreže brez povratnih zank in na mreže s povratnimi zankami. Pri prvih teče signal vedno od vhodnih nevronov proti izhodnim. Vsak vhodni podatek se obravnava kot ločena entiteta. Predhodni podatki na delovanje mreže nimajo vpliva. Drugi tip mrež pa vsebuje t.i. povratne povezave. Pri njih je delovanje odvisno od zaporedja vhodnih signalov oz. od predhodnih vhodnih podatkov. Detajlneje mrež ne bom opisoval, če koga zanima kaj več, naj poišče na guglu (ključne besede pa so napisane na sliki).
Slika 6. Vir: Jain et al., 1996: Artificial neural networks: A tutorial. IEEE.
Preden nevronsko mrežo uporabimo, jo moramo naučiti. Učni proces priredi obtežbe mednevronskih povezav in pa biase tako, da je delovanje mreže ustrezno za rešitev naše naloge. Poznamo tri osnovne principe učenja. Pri prvem tipu učenja - nadzorovanem (supervised) učenju - se povezave urejujejo na podlagi učnih podatkov, ki vsebujejo znane vhodne in pripadajoče izhodne vrednosti. Pred začetkom učenja se vsi prosti parametri mreže (uteži, biasi) postavijo na naključne vrednosti. Algoritem za učenje (najbolj znan je t.i. backpropagation learning algorythm) pa te vrednosti počasi, korak za korakom, prireja tako, da napaka med izračunanimi in pričakovanimi izhodnimi vrednostmi pada proti ničli.
Drugi tip učenja je nenadzorovano učenje (unsupervised), kjer učni algoritem prireja proste parametre mreže zgolj na podlagi vhodnih vrednosti. Osnova tem učnim algoritmom je "tekmovanje za prevlado". Zmagovalni nevron se ojača, drugi nevroni se oslabijo. Na takšen način na koncu dobimo vhodne podatke klasificirane v različne razrede.
Tretji tip učenja je ojačitveno (reinforced) učenje. To je posebna vrsta nadzorovanega učenja, uporabljena predvsem pri učenju časovnih vrst, kjer rezultata neke akcije ne izvemo takoj, ampak šele čez nekaj časa. Primer je igranje šaha. Ali je bila naša strategija uspešna ali ne, ponavadi izvemo šele po nekaj potezah.
Omenil bi še evolucijsko učenje, ki deluje na podoben način, kot evolucijski algoritmi (naključne mutacije, preizkus delovanja, rekombinacija najboljših...).
Zakaj so nevronske mreže uporabne? Nevronske mreže so znane kot univerzalni aproksimatorji, saj lahko aproksimirajo poljubno zvezno funkcijo poljubno natančno, če le imamo dovolj učnih podatkov in dovolj kompleksno mrežo. Pri tem ni omejitev glede števila vhodnih in izhodnih spremenljivk oz. z drugimi besedami, ni omejitve glede dimenzionalnosti prostorov, kjer poteka preslikava. Zaradi dodelanih algoritmov strojnega učenja in hitrih procesorjev so izjemno lahke in priročne za uporabo. Nevronske mreže prebavijo skoraj vse: uporabljeni podatki so lahko pomanjkljivi, podvrženi šumu, napakam, lahko so atrubutivne narave (npr. slab-srednje-dober; grudast-mrvičast-oreškast-poliedričen), ne potrebujemo normalne porazdelitve... Lahko klasificirajo podatke takrat, ko običajna statistika odpove (slika 7). Povratne povezave omogočajo simulacijo zelo kompleksnih dinamičnih sistemov ali pa napovedovanje časovnih vrst (napovedovanje gibanja cen delnic so sanje vsakega ekonomista, samo pazi; nobena izmed firm, ki prodaja programske simulatorje nevronskih mrež za prav ta namen, se ne ukvarja z delnicami). Zmožne so prepoznave črk, slik, govora (pattern recognition). Uporabne so za kontrolo proizvodnih procesov, strojev, robotov, za optimizacijo procesov...
Slika 7.
Težave pri uporabi nevronskih mrež pa so sledeče: podatke moramo normalizirati na interval med 0 in 1 ali pa med -1 in +1. Obstaja večna dilema, kako kompleksna mreža je ravno primerno kompleksna za naš problem. Če uporabimo premalo kompleksno mrežo, problema ne bo mogla rešiti, preveč kompleksna mreža pa se je zmožna učne primere "napiflati" in nima sposobnosti t.i. generalizacije (slika 8) oz. pravilne rešitve primerov, pri katerih mreže nismo učili. Pri učenju mreže nikoli ne vemo, ali smo mrežo naučili dovolj, premalo ali pa morda celo preveč. Na sliki 9 nam krivulja 2 predstavlja padanje napake učnih podatkov, če povečujemo število učnih ciklov, krivulja 2 pa napako, ki jo naredi mreža pri podatkih, katerih nismo uporabili za učenje. Otimalno število učnih ciklov je označeno s krogcem. Povečevanje učnih ciklov vodi v "overfitting", čeprav nam učna napaka še vedno pada. torej smo dosegli popolnoma napačno generalizacijo in tega nam učna napaka sploh ne pokaže.
Slika 8. Vir: Haykin, 1999.
Slika 9. Vir: Kasabov, 1998. Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering. The MIT Press.
Nikoli tudi ne vemo, ali smo dosegli minimalno možno napako. Učenje se nam lahko ustavi na katerem od "lokalnih" minimumov (točka 1 na sliki 10), namesto na globalnem minimumu (točka 2 na sliki 10). Še huje, mreža se nam sploh noče učiti.....
Slika 10. Vir: Boddy & Morris, 1999. Artificial neural networks for pattern recognition. In.: Machine learning methods for ecological applications. Kluwer.
Za konec pa je treba vedeti predvsem to, da nevronske mreže niso nek vsevedni in vsemogočni pripomoček. V prvi vrsti jih omejujejo učni podatki. Saj veste: garbage in, garbage out. Lep primer opisuje zgodbica na tejle povezavi: Neil Fraser: Writing: Neural Network Follies. Prav tako ne morejo aproksimirati nečesa, kar sploh nima vzročne povezave, npr. na podlagi števila ptic selivk izračunati količino frizerskih storitev.
Za konec še nekaj slikic nevronskih mrež z opisi:
Slika 11: večslojni perceptron (Multilayer perceptron - MLP) s 36 vhodnimi nevroni, devetimi procesorskimi ali skritimi (hidden) nevroni in enim izhodnim nevronom (rezultat). Signal poteka od vrha slike proti dnu.
Slika 12: večslojni perceptron (MLP) z dvema procesorskima "skritima" slojema.
Slika 13: razlika med zmožnostjo ločevanja (klasifikacije) med perceptronom, MLP-jem z enim slojem skritih nevronov in MLP-jem z dvema slojema skritih nevronov. Vir: Bishop, 1995.
Slika 14: radial basis function networks oz. mreža z radialnimi nevroni (krogci). Te mreže vedno vsebujejo plast navadnih nelinearnih nevronov za plastjo radialnih nevronov.
Slika 15: samoorganizacijske mreže ali SOM mreže (self-organizing maps). Te mreže učino na podlagi nenadzorovanega učenja. Nevroni tekmujejo za prevlado. Znane so kot zelo zmogljivi klasifikatorji podatkov.
Literatura:
biblija: Bishop, 1995. Neural Networks for Pattern Recognition. Oxford University Press.
Matematika: Haykin, 1999. Neural Networks - a comprehensive foundation. Prentice Hall.
Dober FAQ: ftp://ftp.sas.com/pub/neural/FAQ.html
SLAIS: Slovensko društvo za umetno inteligenco
Free simulator: MemBrain
Free simulator v javi: JavaNNS
Najboljši vir: klik
* linearnost tukaj pomeni, da se jo da opisovati z metodami linearne algebre. Transformacija je torej aditivna in homogena. Več o tem tukaj: klik
Vse je za neki dobr!
- preklicalo razglas: STASI ()
gzibret ::
Še eno sliko sem pozabil pripopati. Gre za en screenshot iz programa MemBrain, in sicer prikaz, na kakšen način deluje prepoznavanje slik.
Na spodnji sliki predstavlja (a) nek ekvivalent CCD čipa oz. 2D polje vhodnih nevronov. Če hočemo zakodirat barvno sliko, pač uporabimo 3 takšne plasti. V tem primeru gre sicer le za eno plast B&W, lahko pa bi bila tudi v grayscale. (b) so plasti procesorskih enot oz. "hidden" layers, v sloju (c), ki je izhodna plast nevronov, pa preberemo rezultat. Če je napisana 0, potem je aktiviran prvi nevron, če 1 potem drugi itd... Če gre za šum ali pa ni napisana nobena cifra, se aktivira ali več nevronov hkrati, ali pa nobeden.
Na spodnji sliki predstavlja (a) nek ekvivalent CCD čipa oz. 2D polje vhodnih nevronov. Če hočemo zakodirat barvno sliko, pač uporabimo 3 takšne plasti. V tem primeru gre sicer le za eno plast B&W, lahko pa bi bila tudi v grayscale. (b) so plasti procesorskih enot oz. "hidden" layers, v sloju (c), ki je izhodna plast nevronov, pa preberemo rezultat. Če je napisana 0, potem je aktiviran prvi nevron, če 1 potem drugi itd... Če gre za šum ali pa ni napisana nobena cifra, se aktivira ali več nevronov hkrati, ali pa nobeden.
Vse je za neki dobr!
snow ::
Lepo je tole. Jaz sem eno raziskovalno nalogo delal z nevronskimi mrežami. Učil sem jih sprva z backpropagation, potem sem prešaltal na evolucijske algoritme.
No zadeva je bila farmacevtsko usmerjena in sicer za proučevanje enih struktur.
Prvi del je obsegal napoved tipa strukture iz sestave (4 komponente), v drugem delu pa smo z nevronsko mrežo interpretirali ene krivulje iz ene mašine (DSC).
No zadeva je bila farmacevtsko usmerjena in sicer za proučevanje enih struktur.
Prvi del je obsegal napoved tipa strukture iz sestave (4 komponente), v drugem delu pa smo z nevronsko mrežo interpretirali ene krivulje iz ene mašine (DSC).
Random mutation plus nonrandom cumulative natural selection - Richard Dawkins
sidd ::
Če se ne motim se z podobnim ukvarja (uporaba nevronskih mrež) g. prof. dr. Jože Balič na Fakulteti za strojništvo v Mariboru. Zadeva sicer gre za napredne obdelovalne sisteme pri proizvodnem strojništvu. Kaj zadnje čase počnejo tam so res osupljive 
Vsa čast za tale članek, zadeva je zelo zanimiva in zelo uporabna.
Vsa čast za tale članek, zadeva je zelo zanimiva in zelo uporabna.
no idea for signature
signed
I
signed
I
vGregor ::
Ima kdo slučajno kaj izkušenj s praktično uporabo nevronskih mrež na finančnem področju? V vsakem opisu namreč zasledim finance oziroma borze kot enega možnih načinov uporabe.
Sam sem se malo igral z modeli za napovedovanje borznih tečajev. Sicer priznam, da z zelo omejenim poznavanjem tematike nevronskih mrež. Uspel sem sestaviti model, ki se je bil sposoben učiti in prepoznavati določene podobne situacije v preteklih podatkih. Vendar je bil rezultat zgolj nekakšna specializacija za napovedovanje preteklih dogodkov. Model se je odrezal odlično na obdobju, na katerem sem ga učil. Pri napovedovanju prihodnosti pa je pogorel.
Takšen rezultat sem sicer tudi pričakoval, ker je realnost na borzi bistveno bolj kompleksna od mojih modelov, zgodovina pa se načeloma ne ponavlja. Vseeno pa me zanima, če je kdo pri tem že kaj bolj napredoval od mene?
Sam sem se malo igral z modeli za napovedovanje borznih tečajev. Sicer priznam, da z zelo omejenim poznavanjem tematike nevronskih mrež. Uspel sem sestaviti model, ki se je bil sposoben učiti in prepoznavati določene podobne situacije v preteklih podatkih. Vendar je bil rezultat zgolj nekakšna specializacija za napovedovanje preteklih dogodkov. Model se je odrezal odlično na obdobju, na katerem sem ga učil. Pri napovedovanju prihodnosti pa je pogorel.
Takšen rezultat sem sicer tudi pričakoval, ker je realnost na borzi bistveno bolj kompleksna od mojih modelov, zgodovina pa se načeloma ne ponavlja. Vseeno pa me zanima, če je kdo pri tem že kaj bolj napredoval od mene?
rasta ::
Model se je odrezal odlično na obdobju, na katerem sem ga učil. Pri napovedovanju prihodnosti pa je pogorel.
Kako se model odreže na učnih podatkih, je nepomembno. V glavnem se ga tako da naučiti tudi na šum.
Razlogi za nedelovanje modela so lahko zelo različni: neustrezna izbira nevronske mreže (premalo/preveč nevronov), prenaučenje (overfitting), zanič je mogoče že sama učna množica (napovedi niso korelirane), itd.
Načeloma pa od tako zašumljenih podatkov, kot so gibanja tečajnic, ne pričakuje nekega slošno uporabnega modela.
gzibret ::
Tukaj je problem, da je na gibanje tečaja delnic delujejo predvsem sociološko/psihološki faktorji. Le-te pa je problem merit in numerično ovrednotit, pa še spremenljivk, ki vplivajo na njih je ohoho veliko.
Ne moreš pa napovedovat gibanja tečajev delnic le na podlagi preteklih tečajev, NUJNO moreš zraven vključit še ogromno drugih faktorjev, pa še takrat je veliko vprašanje, a si sploh vključil taprave. V glavnem, zelo težka naloga, če ne že kar nemogoča.
Glede dobrega prilagajanja podatkom s pomočjo NN - NN ni problem naučit simulirat neke funkcije. Problem je generalizacija in simulacija funkcije, kjer ne poznamo njenega izhoda. Ta naloga je dosti težavnejša.
Če pa je kdo že kaj naredil na področju napovedovanja gibanja cene delnic, pa sigurno ne boš vedel, ker on (če je res tako pameten) bo tiho in lepo služil dinarčke.
Ne moreš pa napovedovat gibanja tečajev delnic le na podlagi preteklih tečajev, NUJNO moreš zraven vključit še ogromno drugih faktorjev, pa še takrat je veliko vprašanje, a si sploh vključil taprave. V glavnem, zelo težka naloga, če ne že kar nemogoča.
Glede dobrega prilagajanja podatkom s pomočjo NN - NN ni problem naučit simulirat neke funkcije. Problem je generalizacija in simulacija funkcije, kjer ne poznamo njenega izhoda. Ta naloga je dosti težavnejša.
Če pa je kdo že kaj naredil na področju napovedovanja gibanja cene delnic, pa sigurno ne boš vedel, ker on (če je res tako pameten) bo tiho in lepo služil dinarčke.
Vse je za neki dobr!
vGregor ::
Vključil sem kar precej makroekonomskih spremenljivk. Sklepal sem, da je bolje preveč spremenljivk kot premalo, ker tiste neprave na naučeni mreži pač ne bi smele imeti prevelikega vpliva na rezultat.
Sicer pa, kolikor jaz razumem NN, bi naj šlo za posnemanje delovanja človeških možganov. Ti pa tako ali tako po pravilu niso preveč dobri pri napovedovanju tečajev. Tudi če bi lahko simulirali človeške možgane do zadnjega nevrona, kar bi gotovo bil dosežek brez primere, ne bi bili kos tistim problemom, ki jim ljudje pač sami nismo kos. Zato bolj vidim uporabo NN na področjih, kjer so naši možgani odlični - zaenkrat prepoznavanje govora, pisave, obrazov, morda v prihodnosti razumevanje jezika (npr. kak semantični Google) ali podobno. Naučiti naše PC-je tisto, kar mi že znamo.
Tako ali tako je dejansko gibanje tečajev preveč kompleksno, pa še vzročno-posledične povezave se praktično nenehno spreminjajo. Osebno sem ravno tako mnenja, da je uspešna uporaba NN v ekonomiji bolj pobožna želja kot kaj drugega. Bil je zgolj zabaven poiskus. Me je pa zanimalo, če se še kdo ukvarja s kakšnimi podobnimi zadevami.
Sicer pa, kolikor jaz razumem NN, bi naj šlo za posnemanje delovanja človeških možganov. Ti pa tako ali tako po pravilu niso preveč dobri pri napovedovanju tečajev. Tudi če bi lahko simulirali človeške možgane do zadnjega nevrona, kar bi gotovo bil dosežek brez primere, ne bi bili kos tistim problemom, ki jim ljudje pač sami nismo kos. Zato bolj vidim uporabo NN na področjih, kjer so naši možgani odlični - zaenkrat prepoznavanje govora, pisave, obrazov, morda v prihodnosti razumevanje jezika (npr. kak semantični Google) ali podobno. Naučiti naše PC-je tisto, kar mi že znamo.
Tako ali tako je dejansko gibanje tečajev preveč kompleksno, pa še vzročno-posledične povezave se praktično nenehno spreminjajo. Osebno sem ravno tako mnenja, da je uspešna uporaba NN v ekonomiji bolj pobožna želja kot kaj drugega. Bil je zgolj zabaven poiskus. Me je pa zanimalo, če se še kdo ukvarja s kakšnimi podobnimi zadevami.
gzibret ::
Jaz NN uporabljam pri interpretaciji (geo)kemičnih podatkov - kemometrija.
Vse je za neki dobr!
rasta ::
Sicer pa, kolikor jaz razumem NN, bi naj šlo za posnemanje delovanja človeških možganov.
Sploh ne. Gre za univerzalni aproksimator, uporablja pa se samo nekatere principe, ki jih uporabljajo tudi naši možgani.
Nevronske mreže so se konec osemdesetih v strokovni javnosti tudi nekoliko otresle pojma "umetne inteligence" in grajenja umetnih možan.
Problem človeškega napovedovanja na borzi je pa bolj problem psihologije.
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Človeški jezik (strani: 1 2 )Oddelek: Znanost in tehnologija | 21084 (17399) | kuall |
| » | IBM razvil umetne nevroneOddelek: Novice / Znanost in tehnologija | 13738 (11357) | antonija |
| » | O čem sanjajo umetni možganiOddelek: Novice / Znanost in tehnologija | 37191 (13188) | lexios |
| » | Petkova predavanja v Hekovniku (Tehnološki park)Oddelek: Novice / Ostalo | 7091 (5088) | Aasimar |
| » | Česa računalnik ne bo nikoli mogel, kar človek pa lahko? (strani: 1 2 3 4 5 )Oddelek: Znanost in tehnologija | 19702 (15964) | gzibret |