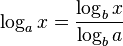Forum » Loža » Izračunaj kot pod katerim funkcija seka os x
Izračunaj kot pod katerim funkcija seka os x
'FireSTORM' ::
Funkcija:
y = log2(x) // logaritem osnove 2 od x
Seka os x v točki 1. Torej je x0 = 1, za izračun kota pa moram izračunat k in potem k vstavit v arctan. Se motim?
Formula za k bi naj bila pa taka: k = (y(x0+dx)-y(x0))/dx
Če vstavim sem in izračunam dobim k = 0, in potem tudi kot 0˚, ampak to ni mogoče ker funkcija seka os x pod kotom nekje 60-75˚ od oka. Že po logiki ne more biti mogoče, kako boš sekal premico ki je pod kotom 0 z drugo premico ki je pravtako pod kotom 0.
Kje za vraga sem se zmotil?
http://www.coolmath.com/graphit/index.h... < - funkcija, vstavi:
2log(x)
y = log2(x) // logaritem osnove 2 od x
Seka os x v točki 1. Torej je x0 = 1, za izračun kota pa moram izračunat k in potem k vstavit v arctan. Se motim?
Formula za k bi naj bila pa taka: k = (y(x0+dx)-y(x0))/dx
Če vstavim sem in izračunam dobim k = 0, in potem tudi kot 0˚, ampak to ni mogoče ker funkcija seka os x pod kotom nekje 60-75˚ od oka. Že po logiki ne more biti mogoče, kako boš sekal premico ki je pod kotom 0 z drugo premico ki je pravtako pod kotom 0.
Kje za vraga sem se zmotil?
http://www.coolmath.com/graphit/index.h... < - funkcija, vstavi:
2log(x)
Those penguins.... They sure aint normal....

luli ::
logaritem daj na skupno osnovo e. Dobljen ulomek odvajaj in vstavi za x=1. Dobil boš k. kot je arctg(k)
'FireSTORM' ::
Zakaj pa na osnovo e? Zakaj nebi raje na 10?
Ehm...nvm.
Zdaj če še se prav spomnim odvajat bi moral dobit tole:
((1/e*ln(x))*ln(2) - ln(x) * (1/e*ln(2)))/(ln(2))^2
Če sem vstavim x = 1 je že prvi ulomek 1/0 in tudi ln(1)=0, torej je zgoraj 0/karkolipačže.
Am I that hopeless? :P
Ehm...nvm.
Zdaj če še se prav spomnim odvajat bi moral dobit tole:
((1/e*ln(x))*ln(2) - ln(x) * (1/e*ln(2)))/(ln(2))^2
Če sem vstavim x = 1 je že prvi ulomek 1/0 in tudi ln(1)=0, torej je zgoraj 0/karkolipačže.
Am I that hopeless? :P
Those penguins.... They sure aint normal....
Zgodovina sprememb…
- spremenil: 'FireSTORM' ()
'FireSTORM' ::
Torej kar mi hočeš povedat je da je to pravilo narobe prepisano?
y = logx(a), y' = 1/(x * ln(a)), a != 1
ln = log osnove e, torej 1/(e * ln(a))
Ali pa jaz samo pravilo narobe razumem.
y = logx(a), y' = 1/(x * ln(a)), a != 1
ln = log osnove e, torej 1/(e * ln(a))
Ali pa jaz samo pravilo narobe razumem.
Those penguins.... They sure aint normal....

luli ::
Pravilo za skupno osnovo :
Torej log2(x)=lnx/ln2
Pravilo za odvajanje ulomka :
(a/b)'=(a'b-ab')/b^2
Torej
((lnx)/(ln2))'=((1/x)ln2-lnx(1/2))/(ln2)^2
Vstavim 1 : (1*Ln2-ln1*1/2)/ln2^2
Torej : Ln2/(ln2)^2
Torej 1/Ln2 = 1.44....
Arctg(1.44....)=55.27°
Upam, da sem računal koliko toliko pravilno
Težko je računat s temi znaki, ni pa i do tega, da bi vzel papir!
Torej log2(x)=lnx/ln2
Pravilo za odvajanje ulomka :
(a/b)'=(a'b-ab')/b^2
Torej
((lnx)/(ln2))'=((1/x)ln2-lnx(1/2))/(ln2)^2
Vstavim 1 : (1*Ln2-ln1*1/2)/ln2^2
Torej : Ln2/(ln2)^2
Torej 1/Ln2 = 1.44....
Arctg(1.44....)=55.27°
Upam, da sem računal koliko toliko pravilno
Težko je računat s temi znaki, ni pa i do tega, da bi vzel papir!

luli ::
Imaš prav, vendar bi se potem primer prehitro rešil.
P.S. : Po resnici sem čisto spregledal, saj sem mu v prvi rešitvi nakazal novo osnovo, potem pa je ulomek obstal v glavi.
P.S. : Po resnici sem čisto spregledal, saj sem mu v prvi rešitvi nakazal novo osnovo, potem pa je ulomek obstal v glavi.
'FireSTORM' ::
Ena ln odvajalna še prosim.
Če je ln(x) = 1/x
potem je
ln(x^2+1) = 1/(x^2+1) ali
= (1/(x^2+1))*(x^2+1)'
Če je ln(x) = 1/x
potem je
ln(x^2+1) = 1/(x^2+1) ali
= (1/(x^2+1))*(x^2+1)'
Those penguins.... They sure aint normal....

luli ::
Odvaja se kot sestavljena funkcija. Se pravi najprej odvod logaritma, potem pa pomnožiš še z odvodom notranje funkcije
Torej : Odvod ln(x^2+1)
je 1/(x^2+1)*2x
Torej : Odvod ln(x^2+1)
je 1/(x^2+1)*2x
Zgodovina sprememb…
- spremenilo: luli ()
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Matematika, pomočOddelek: Šola | 2823 (2085) | TheKekec |
| » | naslednji dve nalogi iz Matematike 2Oddelek: Šola | 2683 (2233) | lebdim |
| » | E (matematična konstanta) (strani: 1 2 3 4 )Oddelek: Šola | 17113 (11577) | Jst |
| » | Dva na x je enako x kvadratOddelek: Šola | 2967 (2608) | G3GANT1C |
| » | Pomoč pri računanju limOddelek: Šola | 1938 (1857) | MaFijec |