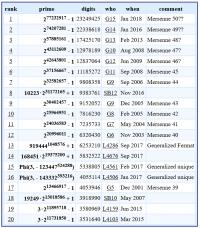
Slo-Tech - Projekt distribuiranega računanja GIMPS, s katerim že od leta 1996 sodelujoči s svojo računsko močjo iščejo velika praštevila, je oktobra letos odkril novo največje znano praštevilo. Luke Durant iz San Joseja je 12. oktobra odkril, da je 2^136.279.841 - 1 praštevilo. Gre za 52. znano praštevilo oblike 2p - 1, ki jih imenujemo Mersennova praštevila. Novo odkrito praštevilo ima 41.024.320 cifer in je za 16 milijonov mest daljše od prejšnjega rekorderja.

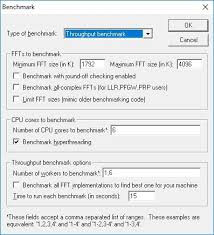
Vsa največja znana praštevila so Mersennova praštevila. Temu botruje posebej učinkovit algoritem za preverjanje praštevilskosti, ki deluje le na teh številih. Lucas-Lehmerjev je edini dovolj učinkovit algoritem, da lahko z današnjo računsko močjo preverimo, ali so večdesetmilijonov mest (v decimalnem zapisu) velika števila praštevila. Projekt GIMPS (Great Internet Mersenne Prime Search) uporablja ta test in je od leta 1996 odkril 18 Mersennovih praštevil.

V programu sodelujejo posamezniki, ki si namestijo odjemalca in prispevajo...

Slo-Tech - Projekt skupnostne znanosti Covid.si, ki se je začel lani ob izbruhu pandemije, je praznoval prvo obletnico obstoja. V tem času se je projekt, ki so ga postavili Črtomir Podlipnik z UL FKKT, Marko Jukić z UM FKKT in Sebastian Pleško, razvil, a glavne aktivnosti so ostale enake. Te so molekulsko sidranje z uporabo distribuiranega računalništva, kar pomeni, da lahko z računsko močjo v njem sodeluje vsakdo.

V projektu je doslej sodelovalo 400 računalnikov, ki so v tem času računali 62 tarč in na njih izvedli prek 837 milijonov neodvisnih eksperimentov molekulskega sidranja (molecular docking). Tako se imenuje računsko ugotavljanje interakcije med molekulami, katerih biološka aktivnost zoper virus se preverja, in različnimi deli virusa. Poleg 400 računalnikov prostovoljcev v projektu uporabljajo tudi računske kapacitete, ki jih je doniral Microsoft na Azuru. S tem so pripravili knjižnico, v kateri je milijarda spojin, ki čakajo na sidranje.

Hkrati so skupaj z Inštitutom za matematiko...

Slo-Tech - Od včeraj smo lahko prepričani, da je 2^82.589.933-1 največje znano praštevilo. Gre za število, ki ima v desetiškem zapisu 24.862.048 mest, tako da zapis v stisnjeni obliki (ZIP) zasede več kot 11 MB. Novo praštevilo je našel Patrick Laroche s Floride, ki sodeluje v projektu skupinskega iskanja Mersennovih praštevil GIMPS. Za nagrado prejme 3000 dolarjev in mesto v zgodovini.

Vsa največja znana praštevila so Mersennova praštevila, kakor se imenujejo praštevila, ki jih lahko zapišemo kot 2^p - 1, kjer je p tudi praštevilo. Ta niso zelo pogosta, a ker zanje poznamo izjemno hiter test, se pri iskanju praštevil lotevamo prav njih. V splošnem je namreč iskanje praštevil počasno in računsko potratno. Projekt GIMPS je imel v zadnjih petnajstih letih neverjetno veliko...

Slo-Tech - Ob koncu leta je projekt GIMPS odkril novo največje znano praštevilo, ki se zapiše 2^77.232.917 − 1 in ima v desetiškem zapisu kar 23,2 milijona cifer. Novo praštevilo je odkril Jonathan Pace 26. decembra, potem ko je na svojem računalniku uspešno poganjal program za njihovo iskanje GIMPS, odkritje pa so potrdili po novem letu. Od zadnjega tovrstnega odkritja minevata dve leti.

Projekt GIMPS, ki teče od leta 1996, je posvečen iskanju Mersennovih praštevil. Gre za posebno vrsto praštevil, ki jih lahko zapišemo kot potenco števila dve,...

Slo-Tech - Praštevila so sicer v prvi vrsti matematična zanimivost in neizmeren vir kratkočasja za matematike, a imajo svojo vlogo tudi v kriptografiji (recimo RSA temelji na enostavno množenja dveh praštevil in težavnosti faktorizacije velikih števil z malo delitelji). Raziskovalca z Univerze Stanford sta odkrila (rokopis članka) zanimiv vzorec v njihovi porazdelitvi, katerega razlog in morebiten pomen še nista jasna.

Iskanje praštevil je torej pomembno tako iz praktičnih kot čisto matematično-estetskih razlogov, zato je koristno vedeti kaj o njihovi porazdelitvi. Vemo, da so praštevila čedalje redkejša (in tudi koliko), a da jih je neskončno mnogo. Ali je posamezno število praštevilo ali sestavljeno, lahko preverimo z različnimi metodami, med katerimi pa so (razen za...

Slo-Tech - Kolaboracija GIMPS je odkrila novo največje praštevilo, ki ima kar 22,3 milijona mest v desetiškem zapisu oziroma pet milijonov več kot prejšnji rekorder. Praštevilo je odkril Curtis Cooper z Univerze Central Missouri, ki je imel v lasti tudi prejšnje tri rekorde. Univerza bo prejela 3000 dolarjev nagrade.

GIMPS je projekt distribuiranega izračunavanja, v katerem sodelujejo prostovoljci s celega sveta v iskanju novih največjih praštevil. Da je teh neskončno mnogo, je pokazal že Evklid, a iskanje čedalje večjih je zaradi omejene računske moči precej zahtevno. Splošen algoritem za preveritev, ali je neko število praštevilo, obstaja, a je popolnoma neuporaben za večja praštevila (celo klasično deljenje je...

Slo-Tech - Fantje pri GIMPS (Great Internet Mersenne Prime Search), ki neprekinjeno teče že od leta 1996, so odkrili novo največje praštevilo na svetu. Te dni so namreč potrdili, da je 25. januarja odkrito število 2^57.885.161-1, ki ga je odkril Curtis Cooper, v resnici praštevilo. Če bi to število izpisali v desetiškem sestavu, bi porabili 17.425.170 mest.

Da je praštevil neskončno mnogo, je pokazal že Evklid, zato je vedno aktualno iskanje največjega znanega praštevila. S tem izrazom označujemo vsa števila,...

The Register - Projekt distribuiranega izračunavanja GIMPS je odkril novo največje praštevilo na svetu. Gre za število 2^43.112.609 − 1, ki ima v decimalnem zapisu dobrih 12 milijonov števk, kar bi v standardno stavljenem tekstu zavzelo 3461 strani, o čemer smo že pisali. Sedaj pa je tudi uradno potrjeno, da GIMPS bo od Electronic Frontier Foundation prejel 100.000 dolarjev nagrade za odkritje tako ogromnega praštevila, od katerih bo šla četrtina v dobrodelne namene, polovica pa na matematični oddelek UCLA, kjer je GIMPS tekel. Obupati pa tudi ostalim iskalcem še ne gre, saj praštevilo z več kot sto milijoni števk prinaša 150.000 dolarjev, tako z milijardo pa 250.000 dolarjev.

Zvedavi bralec bo pri brskanju po seznamih največjih znanih praštevil bržkone hitro zastrigel z ušesi ob ugotovitvi, da so vsa največja znana praštevila oblike 2^p - 1. Zanje imamo celo posebno ime, pravi se jim namreč Mersennova praštevila. To ni posledica kakšne specialne distribucije praštevil na številski osi, marveč...

Slashdot - Mersennova praštevila je prvi raziskoval že Evklid, a so dobila ime po francoskemu učenjaku iz 17. stoletja, Marinu Mersennu. Ta je sestavil seznam praštevil - tj. števil, ki imajo samo dva pozitivna delitelja (sebe in enico) - ki se poleg tega dajo zapisati kot 2ⁿ - 1. To so Mersennova praštevila, ki jih poznamo le 47. Za lovce na enormna praštevila so pomembna zato, ker zanje obstaja eleganten test, ki z malo surove moči določi, ali je neko število Mersennovo praštevilo. Obstaja celo združenje...

Slo-Tech -

Prejšnji teden smo poročali o domnevnem odkritju največjega praštevila na svetu, danes pa je vse skupaj tudi uradno. V projektu distributiranega izračunavanja GIMPS je dr. Martin Nowak iz Nemčije na svojem Pentiumu 4 2,4 GHz dokril 42. znano Mersennovo praštevilo in največje znano praštevilo na svetu sploh. Število 2^25.964.951 - 1 ima 7.816.230 cifer v desetiškem zapisu. Mersennova praštevila so tesno povezana s popolnimi števili (števili, katerih vsota pravih deliteljev je enaka številu samemu), saj velja, da so vsa soda popolna števila oblike 2^{p - 1}(2^p-1), kjer je p eksponent v Mersennovem praštevilu. Lihih popolnih števil še nismo odkrili.

BBC poroča, da so nove Saturne...

več strani -

Da je praštevil, tj. števil, ki imajo zgolj dva pozitivna cela delitelja - sebe in ena, neskončno mnogo, je že pred več kot dva tisoč leti dokazal Evklid in za njim še mnogo matematikov. Zgodba o praštevilih pa se s tem še ne konča, saj matematiki poleg tega, da iščejo čim večja praštevila, poskušajo dokazati tudi nekaj zanimivih domnev.

Zanimiva podmnožica praštevil so Mersennova praštevila, ki jih lahko zapišemo kot 2^p - 1, pri čemer je p tudi praštevilo. Z njihovim iskanjem se ukvarja projekt GIMPS, ki deluje na načelih distributiranega računanja (podobno kot SETI in Folding). Pred dobrima dvema tednoma je Josh Findley odkril enainštiridesto Mersennovo praštevilo 2^{24 036 583} - 1, ki z 7.235.733 znaki v desetiškem zapisu velja za največje praštevilo. Ta petek so uradno potrdili, da gre resnično za praštevilo. Klik!

Še bolj zanimive kot iskanje praštevil pa so domneve o njih. Goldbach je leta 1742 v pismu Eulerju postavil domnevo, da lahko vsako naravno število večje od pet...