Forum » Šola » paralelogram !!
paralelogram !!
cerber ::
Zanima me kako bi narisal paralelogram z naslednjimi podatki: e=8cm f=4cm in kot alfa je 60 stopinj.
perci ::
Nisem bil neki dober v geometriji v srednji soli, ampak kaj tocno te matra?
Zgodovina sprememb…
- odbrisal: perci ()
largie ::
zdi se mi da vem kje je problem, kot je verjetno treba narisat s šestilom. žal se trenutno ne spomnim kako se že to nardi  .
.
LapD ::
[URL=http://img374.imageshack.us/my.php?imag...
Evo skica na hitr pol pa sam kotne funkcije uporabs pa kosinusni izrek
Evo skica na hitr pol pa sam kotne funkcije uporabs pa kosinusni izrek
strictom ::
Edit: wrong window
"Violence is the last refuge of the incompetent" - Salvor Hardin
Zgodovina sprememb…
- spremenila: strictom ()
cerber ::
Problem je v tem, da če najprej narišem alfo in nato v šestilo vzamem e in naredim polkrog ne morem naredit naprej nič več (saj ne vem za dolžino nobene stranice). Če pa začnem z eno od diagonal in jo nato razpolovim, še vedno ne morem narisati druge diagonale, ker ne vem kakšen je kot med njima, vse kar lahko naredim je, da vzamem v šestilo polovico druge diagonale in naredim polkrog - ne morem dokončat lika.
Probajte
lapajne: kotnih funkcij se v začetku drugega letnika še ne učiš
Probajte
lapajne: kotnih funkcij se v začetku drugega letnika še ne učiš
LapD ::
narises e in ker e razpolovi alfo narises kot 30 iz obeh strani. Potem pač potegneš crti v obe smeri ker neves dolzin a in d. Potem razpolovis e in zapicis sestilo v sredino ter levo in desno potegnes polkroga in kjer seka stranici ki si jih prej narisal dobiš ogljišči B in D...dost jasno? 
DOOM_er ::
in ali si ugotovil kaj in kako, ker namreč mene tut zanima kako se nariše
Robots will steal your job. But that's OK
cerber ::
ne
ampak se mi vse bolj zdi, da je nekaj narobe z podatki (bom v ponedeljek vprašal v šoli)
ampak se mi vse bolj zdi, da je nekaj narobe z podatki (bom v ponedeljek vprašal v šoli)
bastadu ::
Paralelogram s takšnimi podatki ne obstaja oz. ga je nemogoče narisati. Če pustimo podatke o diagonalah nespremenjene, mora biti kot alfa enak oz. manjši od 53,13°
Zgodovina sprememb…
- spremenilo: bastadu ()
Fizikalko ::
Dobr no, problem še vedno ostaja.... Naj bo kot pač manjši - kako narisat? Sem tut jest gruntal, pa (še) nič... zajeban!
Fizikalko ::
To že takoj ne more bit prou, ker sploh nisi uporabil podatka za f, brez tega pa paralelogram ne more bit definiran...
Aha, že popravljen post. Ja, najbrž ni rešljivo...
Aha, že popravljen post. Ja, najbrž ni rešljivo...
Zgodovina sprememb…
- spremenilo: Fizikalko ()
Bojevnik ::
če je alfa 60° potem je beta 120°
180°- ( alfa/2 + beta/2) (dobiš kot med e in f).
Narišeš trikotnik s koti alfa/2, beta/2, kot med e in f, a in b tega trikotnika sta e/2 in f/2.
Potem stranici a in b podaljšaš za enkratno dolžino in povežeš točke.
Upam da sem dovolj razumljivo napisal.
180°- ( alfa/2 + beta/2) (dobiš kot med e in f).
Narišeš trikotnik s koti alfa/2, beta/2, kot med e in f, a in b tega trikotnika sta e/2 in f/2.
Potem stranici a in b podaljšaš za enkratno dolžino in povežeš točke.
Upam da sem dovolj razumljivo napisal.
bastadu ::
Bojevnik: Oprosti, ampak čisto si sfalil mimo... Za začetek še enkrat preberi to temo... Hint: diagonala pri paralelogramu ne razpolovi kota

Add:
Add:
a in b tega trikotnika sta e/2 in f/2In od kod ti to?
Zgodovina sprememb…
- spremenilo: bastadu ()
Maister ::
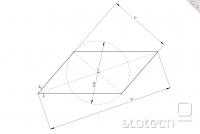
Kaj pa, če bi se spomnili na Talesov izrek? Ta trdi, da vse točke na krožnici gledajo na tetivo pod enakim kotom.
Vzememo diagonalo BD (f, 4cm). Diagonala AC (e) jo seka na polovici, recimo v točki T. Torej je točka A na krožnici s središčem v T in polmerom e/2 (=4 cm, ni važno).
Za pravokotni trikotnik A'TB (kjer je A' točka na tej krožnici, in v splošnem ne tisti A iz paralelograma) lahko izračunamo kot pri A, saj je tg (tega kota) = 1/2 (razmerje katet = f/e), in ta kot je manj kot 30 (stopinj).
Tudi brez uporabe trigonometrije je enostavno videti, da je kot manjši kot 30 - narišemo oba kota (30 stopinj gre s šestilom, trikotnik 1:2 pa tudi
Sklep: s točke A' gledamo diagonalo f pod kotom, manjšim od 60 (stopinj), zato bo vsaka točka, odddaljena od T za e/2 (torej točno vsi kandidati za A) gledala f pod istim kotom. Sledi, da paralelogram (as specified) ne obstaja.
Vzememo diagonalo BD (f, 4cm). Diagonala AC (e) jo seka na polovici, recimo v točki T. Torej je točka A na krožnici s središčem v T in polmerom e/2 (=4 cm, ni važno).
Za pravokotni trikotnik A'TB (kjer je A' točka na tej krožnici, in v splošnem ne tisti A iz paralelograma) lahko izračunamo kot pri A, saj je tg (tega kota) = 1/2 (razmerje katet = f/e), in ta kot je manj kot 30 (stopinj).
Tudi brez uporabe trigonometrije je enostavno videti, da je kot manjši kot 30 - narišemo oba kota (30 stopinj gre s šestilom, trikotnik 1:2 pa tudi
Sklep: s točke A' gledamo diagonalo f pod kotom, manjšim od 60 (stopinj), zato bo vsaka točka, odddaljena od T za e/2 (torej točno vsi kandidati za A) gledala f pod istim kotom. Sledi, da paralelogram (as specified) ne obstaja.
korenje_ver2 ::
> korenje_ver2: Dokaži!
najvecji kot bo lahko, ko bo ena crta na tocko, kjer seka pravokotnica krog (premera 4 cm). druga crta pa mora biti tako da tvori paralelogram. tako se dobi kot najvec 53.13°.
najvecji kot bo lahko, ko bo ena crta na tocko, kjer seka pravokotnica krog (premera 4 cm). druga crta pa mora biti tako da tvori paralelogram. tako se dobi kot najvec 53.13°.
Zgodovina sprememb…
- spremenilo: korenje_ver2 ()
Maister ::
korenje_ver_2,
vsak paralelogram z diagonalama v razmerju e:f=2:1 ima kot pri A 2*arctg(1/2) = 53.13. Ni največjega kota.
V splošnem bo kot pri A enak 2*arctan(f/e).
vsak paralelogram z diagonalama v razmerju e:f=2:1 ima kot pri A 2*arctg(1/2) = 53.13. Ni največjega kota.
V splošnem bo kot pri A enak 2*arctan(f/e).
bastadu ::
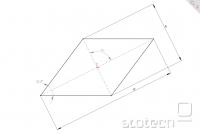
Če je črta tangenta na krožnico (fi 4cm) je res, da je lahko kot alfa največ 49,11°:
Ampak če malo logično pomisliš, bo kot alfa največji takrat, ko bosta e in f med sabo pravokotna; čim bo kot med njima večji oz. manjši od 90°, se bo alfa začel manjšati:
Razumljivo sedaj?
Ampak če malo logično pomisliš, bo kot alfa največji takrat, ko bosta e in f med sabo pravokotna; čim bo kot med njima večji oz. manjši od 90°, se bo alfa začel manjšati:
Razumljivo sedaj?
Zgodovina sprememb…
- zavarovalo slike: STASI ()
bastadu ::
vsak paralelogram z diagonalama v razmerju e:f=2:1 ima kot pri A 2*arctg(1/2) = 53.13. Ni največjega kota.To ni res! Prav bi bilo: Vsak paralelogram z diagonalama v razmerju e:f=2:1 ima največji kot pri A 2*arctg(1/2) = 53.13°. Alfa je pa lahko med 0°- 53,13°
Zgodovina sprememb…
- spremenilo: bastadu ()
Maister ::
ok, priznam svojo napako  ampak dokaza, da je kot največ 53.13, pa še nisem videl (tisto "očitno, da pri takih pogojih" in "logično razmisliti" ne velja kot dokaz).
ampak dokaza, da je kot največ 53.13, pa še nisem videl (tisto "očitno, da pri takih pogojih" in "logično razmisliti" ne velja kot dokaz).
Bojevnik ::
Bojevnik: Oprosti, ampak čisto si sfalil mimo... Za začetek še enkrat preberi to temo... Hint: diagonala pri paralelogramu ne razpolovi kota Add: a in b tega trikotnika sta e/2 in f/2 In od kod ti to?
par mesecev matematike ne dalam pa že vse pozabim
na tistem linku od sinkota piše da se e in f razpolavljata
Zgodovina sprememb…
- spremenilo: Bojevnik ()
DOOM_er ::
e pa f razpolavljata drug drugega diagonali pa ne razpolavljata nobenega kota
Robots will steal your job. But that's OK
bastadu ::
Tako je! Če se diagonali razpolavljata med sabo je nekaj drugega, kot če diagonala razpolavlja kot...
Maister: Ja tistih 'pravih' dokazov niti nikoli nisem znal izpeljevati... Sploh ne vem, kaj bi še moral napisati, da bi veljalo kot dokaz No najbolj važno je, da je res
No najbolj važno je, da je res
Maister: Ja tistih 'pravih' dokazov niti nikoli nisem znal izpeljevati... Sploh ne vem, kaj bi še moral napisati, da bi veljalo kot dokaz
MaFijec ::
Najprej narišemo e, nad to diagonalo načrtamo enakokraki trikotnik, ki ima vrhnji kot 120.
Zapičimo šestilo v vrh trikotnik in naredimo krožnico s polmerom stranske stranice. Zapičimo šestilo v središče osnovnice trikotnika (najdemo ga s šestilom in trikotnikom) , naredimo lok s polmerom f/2, kjer se seka s krožnico, je oglišče A ali C paralelograma. Samo še dopolnimo ...
Upoštevamo dejstvo, da je središčni kot 2x obodni kot.
Tole je recimo naloga za osnovnošolsko tekmovanje iz matematike :=).
Zapičimo šestilo v vrh trikotnik in naredimo krožnico s polmerom stranske stranice. Zapičimo šestilo v središče osnovnice trikotnika (najdemo ga s šestilom in trikotnikom) , naredimo lok s polmerom f/2, kjer se seka s krožnico, je oglišče A ali C paralelograma. Samo še dopolnimo ...
Upoštevamo dejstvo, da je središčni kot 2x obodni kot.
Tole je recimo naloga za osnovnošolsko tekmovanje iz matematike :=).
bastadu ::
Bojevnik: Še vedno ne kapiram
MaFijec: Bravo! Pravkar si dokazal da nimaš pojma Prvo kot prvo:
Prvo kot prvo:
MaFijec: Bravo! Pravkar si dokazal da nimaš pojma
Zapičimo šestilo v vrh trikotnik in naredimo krožnico s polmerom stranske stranice.Je kdo mogoče omenil podatek o polmeru stranske stranice? Znani sta samo obe diagonali in kot alfa... in kot že povedano in ilustrirano s slikicami, paralelogram ne obstaja
Zgodovina sprememb…
- spremenilo: bastadu ()
ch'i ::
Alfa (ki ima vrh v krajišču diagonale e) je največji, ko je kot med diagonalama Π/2.
BŠS rečemo, da je e daljša diagonala, kot med e in f pa je med 0 in Π/2. Malo poračunamo (verjetno se da tudi bolj elegantno, pa ni potrebno):
F[a_, e_, f_] := ArcTan[(f/e) Sin[a]] + ArcTan[(f Sin[a])/(e + f Cos[a])] (kot med diagonalama je a).
Iz lastnosti funkcij vidimo, da ima cela reč maksimum ravno pri Π/2 (končna funkcija je naraščajoča, ker je arctan naraščajoč, prav tako tudi oba argumenta, dokaz prepuščam zainteresiranemu bralcu ).
).
QED.
[ch'i, OwcA]
BŠS rečemo, da je e daljša diagonala, kot med e in f pa je med 0 in Π/2. Malo poračunamo (verjetno se da tudi bolj elegantno, pa ni potrebno):
F[a_, e_, f_] := ArcTan[(f/e) Sin[a]] + ArcTan[(f Sin[a])/(e + f Cos[a])] (kot med diagonalama je a).
Iz lastnosti funkcij vidimo, da ima cela reč maksimum ravno pri Π/2 (končna funkcija je naraščajoča, ker je arctan naraščajoč, prav tako tudi oba argumenta, dokaz prepuščam zainteresiranemu bralcu
QED.
[ch'i, OwcA]
Zgodovina sprememb…
- spremenila: ch'i ()
Nejc Pintar ::
danes odkril:
najprej narišemo f
s šestilom narišemo krožnico v razpolovišču diagonal (možnosti za e)
narišemo tangento na krožnico iz točke A
iz tangente naredimo 60°
na presečišču dobimo točko D
na stičišču tangente in krožnice je točka B
narišemo vzporednice
p.s. sliko dobite čez 5min
najprej narišemo f
s šestilom narišemo krožnico v razpolovišču diagonal (možnosti za e)
narišemo tangento na krožnico iz točke A
iz tangente naredimo 60°
na presečišču dobimo točko D
na stičišču tangente in krožnice je točka B
narišemo vzporednice
p.s. sliko dobite čez 5min
Lahko je biti prvi, če si edini!
Nejc Pintar ::
s točko A začneš
samo je grda slika, niso vzporedne stranice, na papirju mi je ratal čist lepo
p.s. pa spodnja stranica a bi morala bit tangenta, samo mi ni ratal, se bom probou potrudt
samo je grda slika, niso vzporedne stranice, na papirju mi je ratal čist lepo
p.s. pa spodnja stranica a bi morala bit tangenta, samo mi ni ratal, se bom probou potrudt
Lahko je biti prvi, če si edini!
Zgodovina sprememb…
- spremenil: Nejc Pintar ()
Fizikalko ::
Nič jasno - kje maš kakšne tangente? Kako si se odločil za smer stranice a? Pa e inf si pomešal...
Nejc Pintar ::
Zdaj je lepše, poimenovanje stranice pa ni tukaj sploh problem.
Najprej narišemo f(e) iz razpolovišča naredimo krožnico ki določa e(f), nato iz točke A narišemo tangento na krožnico, na stičišču tangente in krožnice je B. nato narišemo kot alfa, in na stičišču krožnice in premice nastane točka D, nato samo še potegnemo vzporednice!
Najprej narišemo f(e) iz razpolovišča naredimo krožnico ki določa e(f), nato iz točke A narišemo tangento na krožnico, na stičišču tangente in krožnice je B. nato narišemo kot alfa, in na stičišču krožnice in premice nastane točka D, nato samo še potegnemo vzporednice!
Lahko je biti prvi, če si edini!
OwcA ::
Em, dolžine se nekako ne ujmejo (e = 8 cm, f = 4 cm). 
Otroška radovednost - gonilo napredka.
Zgodovina sprememb…
- spremenilo: OwcA ()
Fizikalko ::
In kako si zagotovil pravo dolžino f-ja oz. e-ja? Tako dobljenoa točka D namreč ni ravno nasproti Bja glede na krožnico, tako da vmes ni dolžina f oz. e..
Nejc Pintar ::
odkril sem drug problem, za f sem vzel 6cm, bom poskusil se z 8cm, na tejle sliki pa ni sredina ker mi je disk crknil in imam zasilno resitev, kamor pa ne morem namescat programov, s programi ala ms. paint pa ne morem ravno narisat sredisca, etc.
Lahko je biti prvi, če si edini!
DOOM_er ::
Z nejcem sva tole risala ob kofetu in on je pogruntal kako se lahko to nariše. Narisal je in izmerila sva use koter stranice diagonale nakar sva še na moji sliki izmerila vse in stvar se je izšla.
Potek:
1. izberemo si točko A kjerkoli na listu papirja
2. narišemo diagonalo v katerokoli smer in konec diagonale označimo s črko C, ki je točka
3. Poiščemo razpolovišče diagonale F (ta dolga diagonala), in razpolovišče označimo z R
4. v R zapičimo šestilo in odmerimo 2cm ter narišemo poln krog
5. iz točke A narišemo tangento na krožnico
6. tam kjer se tangenta dotika krožnice označimo točko B
7. pri točki A odmerimo 60° in potegnemo črto
8. tam kjer drugič seka ta poltrak krožnico označimo točko D
9. Zdaj pa samo še potegtnemo vzporednice skoz točke BC in CD
10. viola dobimo paralelogram
11. preverite vse dolžine in presenečeni boste da sta obe diagonali pravilni da sta stranici a in c enako dolgi ter vzporedni ter da sta stranici b in d vzporedni in enako dolgi
QED
Potek:
1. izberemo si točko A kjerkoli na listu papirja
2. narišemo diagonalo v katerokoli smer in konec diagonale označimo s črko C, ki je točka
3. Poiščemo razpolovišče diagonale F (ta dolga diagonala), in razpolovišče označimo z R
4. v R zapičimo šestilo in odmerimo 2cm ter narišemo poln krog
5. iz točke A narišemo tangento na krožnico
6. tam kjer se tangenta dotika krožnice označimo točko B
7. pri točki A odmerimo 60° in potegnemo črto
8. tam kjer drugič seka ta poltrak krožnico označimo točko D
9. Zdaj pa samo še potegtnemo vzporednice skoz točke BC in CD
10. viola dobimo paralelogram
11. preverite vse dolžine in presenečeni boste da sta obe diagonali pravilni da sta stranici a in c enako dolgi ter vzporedni ter da sta stranici b in d vzporedni in enako dolgi
QED
Robots will steal your job. But that's OK
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | GeometrijaOddelek: Šola | 4687 (3760) | invisable |
| » | Matematika-pomoč ( hitro)Oddelek: Šola | 1884 (1546) | lebdim |
| » | Načrtovanje trikotnika(nujno)Oddelek: Šola | 4989 (4737) | euler |
| » | geometrijska konstrukcijaOddelek: Šola | 4251 (3454) | euler |
| » | Geometrijska konstrukcijaOddelek: Šola | 4693 (4693) | euler |