☰

» »

Streha

Streha

BRBR ::

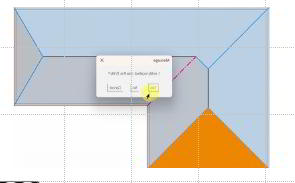
https://i.postimg.cc/h4Mt0Cy8/tmp.jpg

https://i.postimg.cc/h4Mt0Cy8/tmp.jpg



Če je spodnja stranica oranžnega trikotnika 11 m, koliko sta ostali dve stranici ?
Naklon strehe mora biti 45 stopinj.
Never underestimate the power of idiots in large groups.
  • spremenil: BRBR ()

Anney ::

cca 25+15
Obstajata samo dva načina kako živeti svoje življenje:
Prvi pravi, da nič ni čudež, drugi pa, da vse je čudež.

jarre ::

Enakokraki trikotnik, spodnja kota sta 45 stopinj, zgornji je torej 90 stopinj. Neznani stranici ("A") sta enako dolgi, spodnja stranico označimo s "C" in je zato formula za izračun ene stranice: a=c/kv.koren2 (ne da se mi iskati kako se pravilno zapišejo matematični znaki)

Torej je vsaka stranica dolga približno 7,78 metra.

bastadu ::

BRBR je izjavil:

https://i.postimg.cc/h4Mt0Cy8/tmp.jpg

https://i.postimg.cc/h4Mt0Cy8/tmp.jpg



Če je spodnja stranica oranžnega trikotnika 11 m, koliko sta ostali dve stranici ?
Naklon strehe mora biti 45 stopinj.

Stranici sta dolgi 9,53m.

bastadu ::

jarre je izjavil:

Enakokraki trikotnik, spodnja kota sta 45 stopinj, zgornji je torej 90 stopinj. Neznani stranici ("A") sta enako dolgi, spodnja stranico označimo s "C" in je zato formula za izračun ene stranice: a=c/kv.koren2 (ne da se mi iskati kako se pravilno zapišejo matematični znaki)

Torej je vsaka stranica dolga približno 7,78 metra.

Malo si pomešal, OP je napisal, da je naklon strehe 45°, ne pa kot med znano in neznano stranico trikotnika ...

mojca ::

Bastadu ima prav. Dolžina ostalih dveh stranic je a * sqrt(3)/2 = 9.52628 m. To enostavno izračunaš s Pitagorovim izrekom oz. kot diagonalo kocke z osnovno stranico 5,5 m.

Bizkit45 ::

Po cem sklepate da je kateri od kotov 90 stopinj?

bemfa ::

Po tem da je naklon 45° in da so vsi koti skupaj 180° (45+45+90).

bastadu ::

Še 1x: 45° je naklon strehe, ne pa kot katerekoli stranice dotičnega trikotnika ...

Zgodovina sprememb…

  • spremenilo: bastadu ()

bemfa ::

In kolikšen je kot trikotnika? Razsvetli nas neumneže, da bomo vedeli za drugič.

bastadu ::

54,74 + 54,74 + 70,53°

bemfa ::

In to si zračunal kako?

bastadu ::

klik

bemfa ::

Aja, na štirikapnico nisem pomislil, sem si predstavljal dvokapnico.

Bizkit45 ::

Neki si hotu, pa ni slo.. :)

mirator ::

@BRBR ponavadi daje primere z vsaj enim dvomljivim podatkom.
V tem primeru ni vseeno ali je višina trikotnika v z-osi koordinatnega sistema ali pod kotom. Drugače povedano, ali gre za streho s čopom ali ne (iz tlorisa je razvidno, da gre za čop). Torej s čopom manjka en podatek, če pa je to samo čelna stran strehe, je naloga, kot so jo nekateri že prikazali, enostavno rešljiva. V tem primeru (če katete označimo z a in znano stranico s c)je kateta pač enaka c/2*koren(2).
Rezultat je torej: 14,85

Zgodovina sprememb…

  • spremenil: mirator ()

Ijus ::

tole bi bilo najlažje izmeriti v kakem 3D modeling programu :))
travnik pa gasa pa pol SHIFT+DEL :D
Corpse & Mrhovina & Jožica, Inc.
https://soundcloud.com/rising-night-wave
https://soundcloud.com/extus

mirator ::

mirator je izjavil:

V tem primeru (če katete označimo z a in znano stranico s c)je kateta pač enaka c/2*koren(2).
Rezultat je torej: 14,85

Žal sem za c napačno vzel 21cm, namesto 11cm. Tako je prava vrednost 7,78 cm.

BRBR ::

Jaz glasujem za 9.51961m. Najbrž imam prav, ker se ne smem zajebat (-:
Hvala za namige.
Never underestimate the power of idiots in large groups.

bastadu ::

Me pa res zanima, kako si prišel do številke 9.51961m ...

BRBR ::

bastadu je izjavil:

Me pa res zanima, kako si prišel do številke 9.51961m ...



9,53m je tvoj izraćun, torej tam, tam. Jaz sem prišel do tega s tole igračo:
Never underestimate the power of idiots in large groups.

bastadu ::

Torej z orodjem za izračun pravokotnega trikotnika si izračunal dolžino stranice trikotnika, katerega noben kot ni 90°, potem že mora biti prav, ane? 9,53m je čisto pravilen zaokrožen rezultat, če želiš na več decimalk natančnosti, pa samo povej ... Namreč tvojih 9.51961m ni pravilen, ampak samo približen rezultat ...

mirator ::

BRBR je izjavil:

Jaz glasujem za 9.51961m. Najbrž imam prav, ker se ne smem zajebat (-:
Hvala za namige.

Če se ne smeš zajebavat, potem ne glasuj, ampak izračunaj.
Imaš enakokraki trikotnik, katerega katete so nasproti znani osnovni stranici pod kotom 45°. Višina tega trikotnika je enaka polovici osnovne sranice (v = c/2), zato lahko uporabiš pitagorovo pravilo: (c/2)2+(c/2)2=a2 => a=c/2*koren(2).
Če ne verjameš, si nariši.

nejc_nejc ::

mirator je izjavil:

mirator je izjavil:

V tem primeru (če katete označimo z a in znano stranico s c)je kateta pač enaka c/2*koren(2).
Rezultat je torej: 14,85

Žal sem za c napačno vzel 21cm, namesto 11cm. Tako je prava vrednost 7,78 cm.

V tlorisu.

BRBR ::

mirator je izjavil:

BRBR je izjavil:

Jaz glasujem za 9.51961m. Najbrž imam prav, ker se ne smem zajebat (-:
Hvala za namige.

Če se ne smeš zajebavat, potem ne glasuj, ampak izračunaj.
Imaš enakokraki trikotnik, katerega katete so nasproti znani osnovni stranici pod kotom 45°. Višina tega trikotnika je enaka polovici osnovne sranice (v = c/2), zato lahko uporabiš pitagorovo pravilo: (c/2)2+(c/2)2=a2 => a=c/2*koren(2).
Če ne verjameš, si nariši.


Med zajebat in zajebavat je bistvena razlika. Tam ni nobenega kota 45, kjer ga ti vidiš. Če ne verjameš si nariši.
Če ne dobiš +/- 9.5, potem nisi dobil nič. Kot ti je že en povedal, nekaj se ubadaš s tlorisom, tam, kjer tloris nima veze.
Tole tule je 3D. Chill.
Never underestimate the power of idiots in large groups.

Zgodovina sprememb…

  • predlagal izbris: mirator ()

Bizkit45 ::

Trikotnik pravokotno na tloris je ravna crta (daljica).

mirator ::

BRBR je izjavil:


Med zajebat in zajebavat je bistvena razlika. Tam ni nobenega kota 45, kjer ga ti vidiš. Če ne verjameš si nariši.
Če ne dobiš +/- 9.5, potem nisi dobil nič. Kot ti je že en povedal, nekaj se ubadaš s tlorisom, tam, kjer tloris nima veze.
Tole tule je 3D. Chill.

Tam ni nobenega kota 45, kjer ga ti vidiš.
Tole je tvoje osnovno vprašanje:
Če je spodnja stranica oranžnega trikotnika 11 m, koliko sta ostali dve stranici ?
Naklon strehe mora biti 45 stopinj.

Težko ti je pomagati, če ne daš eksaktnih podatkov in očitno ne veš, kaj želiš.
Torej ne gre za naklon strehe ampak naklon rumenega trikotnika. Ne vem, ali res iščeš velikost stranice ali višino tega trikotnika? To, kar ti je izračunal @bastadu je višina, stranica tega trikotnika pri tej višini pa je enaka osnovni stranici torej 11cm.
Pa še okoli 3d. Ko iščeš veličine v 1d (dolžine), jih izračunaš iz 2d (prerezi). In pri tem ni nobenega tlorisa ali narisa pač vse veličine morajo ležati na isti ravnini.

nejc_nejc ::

Podatki so čisto ok. V tlorisu ne moreš razen z besedo, oznako, opisati naklona.

mirator ::

Da se bomo bolje razumeli, kaj kateri podatek pomneni.
http://gradovivoblakih.blogspot.com/201...
V osnovnem podatku sem jaz naklon strehe pač razumel naklon, kot je prikazan v linku. Če bi OP napisal, da je trikotnik pod naklonom 45°, bi bilo povsem drugače.
Seveda samo iz tlorisa ne moreš direktno ugotoviti naklona, ga pa lahko če imaš tloris v merilu in je višina tlorisnega trikotnika projekcija prave višine in ko maš podan tudi kot, zlahka izračunaš ostale neznanke.

@bastadu - se ti opravičujem. Tvoj izračun je pravilen.

nejc_nejc ::

Če smo že "detaljni", to ni čop, kot si ga omenil v tekstih ter prikazal v skici na linku.

Itak brezveze, malo za kravžljat možgane.
Odlična nalogica.

Vredno ogleda ...

TemaSporočilaOglediZadnje sporočilo
TemaSporočilaOglediZadnje sporočilo
»

Matematika - trapez

Oddelek: Šola		229033 (6036) Yacked2
»

Geometrija

Oddelek: Šola		194103 (3176) invisable
»

matematika, geometrije v ravnini, telesa

Oddelek: Šola		203285 (2654) manniac
»

Enakokrak trikotnik

Oddelek: Šola		81506 (1344) lebdim
»

matematika-pomoč

Oddelek: Šola		62356 (2107) Math Freak

Več podobnih tem