Forum » Elektrotehnika in elektronika » Problem pri reševanju nalog z integrali
Problem pri reševanju nalog z integrali
stromkekec ::
Pozdravljeni,
se študent 1 letnika FE v LJ, prihajam pa iz tehnične šole.
problem mi nastopi pri reševanju nalog, kjer se uporabljajo integrali
na primer pri tej nalogi
Poznam integral za mag. pretok. Vem da vnese namesto B-ja enačbo za mag. pols. jakost zunaj vodnika, vendar kaj potem izbere za da?
(l-x) po kakšni logiki. tega nikakor ne morem dojet.
isto mi nastopi problem pri tej nalogi
Vem da vzame za osnovo biot savarov zakon, vendar ne vem kaj vstavi za objekt in dB
mi lahko lepo prosim kdo razloži, da se mi vsaj malo zbistrijo stvari glede teh integralov.
Hvala za pomoč že v naprej
se študent 1 letnika FE v LJ, prihajam pa iz tehnične šole.
problem mi nastopi pri reševanju nalog, kjer se uporabljajo integrali
na primer pri tej nalogi
Poznam integral za mag. pretok. Vem da vnese namesto B-ja enačbo za mag. pols. jakost zunaj vodnika, vendar kaj potem izbere za da?
(l-x) po kakšni logiki. tega nikakor ne morem dojet.
isto mi nastopi problem pri tej nalogi
Vem da vzame za osnovo biot savarov zakon, vendar ne vem kaj vstavi za objekt in dB
mi lahko lepo prosim kdo razloži, da se mi vsaj malo zbistrijo stvari glede teh integralov.
Hvala za pomoč že v naprej
Unilseptij ::
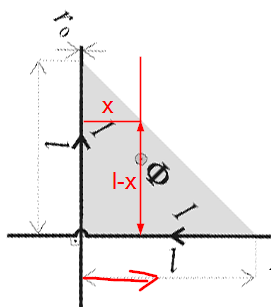
Za prvo nalogo si predstavljaj vse skupaj zarotirano za 45 stopinj tako, da vodnika sovpadata s koordinatnima osema. Potem hitro vidiš, da integral po površini treče po pasovih širine dx in višine (l-x).
Za drugo nalogo pa imaš vse že narisano... Kaj točno te zanima?
Za drugo nalogo pa imaš vse že narisano... Kaj točno te zanima?
darkolord ::
Verjetno si ne predstavljaš najbolje, kako integral "izgleda".
Pri (enojnem) integralu računaš neko površino, ne glede na to, v katerem koordinatnem sistemu je zadeva, ali kako je poimenovana ali obrnjena.
Če se v prvem primeru po eni koordinatni osi premakneš za nek poljuben "x", koliko je vrednost na drugi osi? (l-x). Z integralom pa se pomikaš od roba vodnika (r0) do l po infinitezimalnih (neskončno majhnih) korakih/pasovih širine dx. Površina enega takega pasu je dx * (l-x).
Celotna površina pod trikotnikom je pa seštevek vseh teh pasov površine dx * (l-x).
Pri drugi nalogi je zelo podobno. Pomikaš se po y po pasovih širine dy in računaš seštevek vseh (dy / p) po celotni dolžini.
Pri integralih je po mojem najtežji del ravno to, da si zadeve vizualno ne predstavljaš. Ko poštekaš, da je to samo malo bolj napreden "a * b", postane vse precej bolj jasno in enostavnejše.
Pri (enojnem) integralu računaš neko površino, ne glede na to, v katerem koordinatnem sistemu je zadeva, ali kako je poimenovana ali obrnjena.
Če se v prvem primeru po eni koordinatni osi premakneš za nek poljuben "x", koliko je vrednost na drugi osi? (l-x). Z integralom pa se pomikaš od roba vodnika (r0) do l po infinitezimalnih (neskončno majhnih) korakih/pasovih širine dx. Površina enega takega pasu je dx * (l-x).
Celotna površina pod trikotnikom je pa seštevek vseh teh pasov površine dx * (l-x).
Pri drugi nalogi je zelo podobno. Pomikaš se po y po pasovih širine dy in računaš seštevek vseh (dy / p) po celotni dolžini.
Pri integralih je po mojem najtežji del ravno to, da si zadeve vizualno ne predstavljaš. Ko poštekaš, da je to samo malo bolj napreden "a * b", postane vse precej bolj jasno in enostavnejše.
stromkekec ::
Najprej HVALA za odgovor :)
to potem pomeni, če povem grafiično, da seštevam te male plošince dx od
(l-l) ~ 0, DO (l-r) ~ skoraj 0
in v bistvu pol z tem seštejem celo ploščino tega trikotnika ?
to potem pomeni, če povem grafiično, da seštevam te male plošince dx od
(l-l) ~ 0, DO (l-r) ~ skoraj 0
in v bistvu pol z tem seštejem celo ploščino tega trikotnika ?
Zgodovina sprememb…
- predlagalo izbris: luuxiii ()
darkolord ::
Ne razumem čisto najbolje.
Iz katere smeri se pomikaš kam, je v bistvu čisto vseeno, važno da zajameš celo površino. Poskusiš pa štartati iz smeri, da ti bo najlažje.
Najlažje je npr. takole:
Od leve proti desni se pomikaš od x = r0 (od zunanjega oboda vodnika) do x = l. Za vsak ta x je f(x) = l-x. Če se pomikaš po pasovih širine dx, je ploščina vsakega takega pasu pod trikotnikom dx*(l-x).
Iz katere smeri se pomikaš kam, je v bistvu čisto vseeno, važno da zajameš celo površino. Poskusiš pa štartati iz smeri, da ti bo najlažje.
Najlažje je npr. takole:
Od leve proti desni se pomikaš od x = r0 (od zunanjega oboda vodnika) do x = l. Za vsak ta x je f(x) = l-x. Če se pomikaš po pasovih širine dx, je ploščina vsakega takega pasu pod trikotnikom dx*(l-x).
stromkekec ::
Verjetno si ne predstavljaš najbolje, kako integral "izgleda".
Pri (enojnem) integralu računaš neko površino, ne glede na to, v katerem koordinatnem sistemu je zadeva, ali kako je poimenovana ali obrnjena.
HVALA za odgovor in pomoč :)
v bistvu res ugotavljam da me to muči najbolj muči (vem da to ni več srednja šola, sam dokler ne osvojiš, se mučiš)
Če se v prvem primeru po eni koordinatni osi premakneš za nek poljuben "x", koliko je vrednost na drugi osi? (l-x)
ja Y se zmanjša ravno za toliko kolikor se zmanjša x (če gledam v smeri puščice)
torej površina enega tega "trikotnika" je infitizimalno mali pasek dx * (l-x)
Pri drugi nalogi je zelo podobno. Pomikaš se po y po pasovih širine dy in računaš seštevek vseh (dy / p) po celotni dolžini.
Če prav razumem...torej dx, je ta mali delček k je obkoržen rdečo, potem pa gledam vrednost sile v vsakem delčku, k ga pomikam od spodaj (-a) do zgoraj (a).
potem je zato I/2a ?
Ne razumem čisto najbolje.
Iz katere smeri se pomikaš kam, je v bistvu čisto vseeno, važno da zajameš celo površino. Poskusiš pa štartati iz smeri, da ti bo najlažje.
Najlažje je npr. takole:
Od leve proti desni se pomikaš od x = r0 (od zunanjega oboda vodnika) do x = l. Za vsak ta x je f(x) = l-x. Če se pomikaš po pasovih širine dx, je ploščina vsakega takega pasu pod trikotnikom dx*(l-x).
malo si me prehitel
tak kot sm zgoraj napisal...vidim da sm ujel point tega trikotnika :D...
za tuk k se x zmanjša (x-l), za tulk se tut y zmanjša
Hvala !
Zgodovina sprememb…
- spremenilo: stromkekec ()
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Smiselnost integralov s drugim diferencialom (strani: 1 2 )Oddelek: Šola | 14101 (12661) | Unknown_001 |
| » | Analiza vezjaOddelek: Šola | 3280 (2651) | int47 |
| » | Burnout ParadiseOddelek: Igre | 2027 (813) | Teo0 |
| » | photoshop cs3Oddelek: Programska oprema | 1336 (1044) | Wolfman |
| » | [c++] problem: pretvorba iz malih v velike crkeOddelek: Programiranje | 2380 (2027) | Makina |