Forum » Šola » Problem z integralom
Problem z integralom
Sergio ::
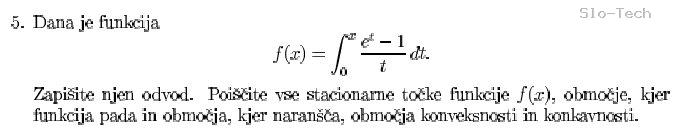
Navodilo naloge mi je popolnoma jasno, težava je le, da zgornjega izraza ne znam integrirati.
Če se ne motim, bi moral ven dobiti integralni sinus ter logaritem, a nisem prepričan.
Vsaka pomoč je zelo dobrodošla :)
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
- spremenil: Sergio ()
Sergio ::
Am, sedaj razmišljam. Mi jo je sploh potrebno integrirati? Dvomim... Kvečjemu odvajati bi jo moral še enkrat....
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
frudi ::
sicer je moja analiza že daleč, ampak od oka bi rekel, da je iskani odvod kar (e^x-1)/x.
1ACDoHVj3wn7N4EMpGVU4YGLR9HTfkNhTd... in case I've written something useful :)
DavidJ ::
Tale funkcija je čudna.. nekako sta pol in stacionarna točka enaka? 
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
jeti51 ::
Sergio, funkcijo moraš odvajati. Saj ti že na začetku lepo piše, zapiši njen odvod. 
Ker vemo (beri: če se prav spomnim ), da je "odvod po x" integrala v mejah od 0 do x kar sama funkcija, ki je pod integralom, je odvod te naše funkcije enak (e^x - 1)/x. Stacionarne točke, pole, intervale naraščanja, padanja, konveksnost ipd. pa zdaj ni težko izračunati.
), da je "odvod po x" integrala v mejah od 0 do x kar sama funkcija, ki je pod integralom, je odvod te naše funkcije enak (e^x - 1)/x. Stacionarne točke, pole, intervale naraščanja, padanja, konveksnost ipd. pa zdaj ni težko izračunati. 
Ker vemo (beri: če se prav spomnim
Sergio ::
jeti51: hvala ;)
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
DavidJ ::
Mene zanima... Tale odvod ima ničlo in pol v isti točki. y=0.
Kaj zdej?
Kaj zdej?
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
Sergio ::
Če se ne motim, uporabiš L'Hospitalovo pravilo ter odvajaš števec ter imenovalec, ter dobiš 1. Zadeva torej nima niti ničle niti pola, temveč limitira proti vrednosti 1.
Tako grem jaz, tako gre vsak, kdor čuti cilj v daljavi:
če usoda ustavi mu korak,
on se ji zoperstavi.
če usoda ustavi mu korak,
on se ji zoperstavi.
DavidJ ::
Uhm, očitno tole gre izven okvirja srednješolske matematke.
Samo stacionarne točke so ničle prvega odvoda... če pa tole še 1x odvajaš pa dobiš drugi odvod?
Bedno vprašanje najbrž..
Samo stacionarne točke so ničle prvega odvoda... če pa tole še 1x odvajaš pa dobiš drugi odvod?
Bedno vprašanje najbrž..
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
jeti51 ::
davids: ni bedno vpšrašanje, v srednji šoli se tega pač ne učite.
L'Hospitalovo pravilo lahko uporabljaš pri računanlju raznih limit.
Recimo poglejmo vrednost naše funkcije, ko gre x proti 0:
lim(x->0) (e^x-1)/x = ???
Imamo problem, ker je 0 v imenovalcu, zato števec in imenovalec odvajamo. Po L'Hospitalovem pravilu se limita izraza s tem ne bo spremenila:
??? = lim(x->0) (e^x - 0)/1 = lim(x->0) e^x = 1
Tako pridemo do rezultata.
L'Hospitalovo pravilo lahko uporabljaš pri računanlju raznih limit.
Recimo poglejmo vrednost naše funkcije, ko gre x proti 0:
lim(x->0) (e^x-1)/x = ???
Imamo problem, ker je 0 v imenovalcu, zato števec in imenovalec odvajamo. Po L'Hospitalovem pravilu se limita izraza s tem ne bo spremenila:
??? = lim(x->0) (e^x - 0)/1 = lim(x->0) e^x = 1
Tako pridemo do rezultata.
pivmik ::
To morem jazst znat za popravni od matematike, tako da je v okviru serdnješolske matematike.
Poskustite s substitucijo.
Poskustite s substitucijo.
LP, Gregor GRE^
DavidJ ::
Odvajat po pravilu tega Francuza ni v srednji šoli. So pa limite in integrali. 
No, si bom v jeseni tole mal razjasnu.
No, si bom v jeseni tole mal razjasnu.
"Do, or do not. There is no 'try'. "
- Yoda ('The Empire Strikes Back')
- Yoda ('The Empire Strikes Back')
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Matematika, pomočOddelek: Šola | 2823 (2085) | TheKekec |
| » | Matematika limite - pomočOddelek: Šola | 2329 (1902) | giaro |
| » | LimiteOddelek: Šola | 3245 (2507) | lebdim |
| » | Naloga - limiteOddelek: Šola | 2264 (1860) | Janac |
| » | Limita funkcijeOddelek: Šola | 3319 (2545) | IceCold |