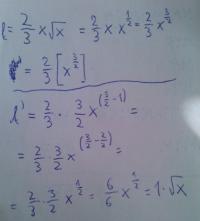Forum » Šola » Odvajanje
Odvajanje
Mario2 ::
Odvedite funkcijo (2)/(3)xsqrt(x). Če modificiramo dobimo dve tretjini x na tri polovice. Eksponent tri polovice me pri odvajanju zelo moti. Rezultat je koren x. Hvala za pomoč!
- predlagalo izbris: [D]emon ()
Yacked2 ::
Kaj te moti ?
Takšna je funkcija ? http://www.wolframalpha.com/input/?i=%2...
2/3 lahko prepišemo, ker je (c*f(x))' = c*f'(x)
koren pretvoriš v potenco 1/2 in daš exsponenta na skupni imenovalec 3/2 torej, nato pa odvajaš in dobiš 3/2 * x^ (3/2 -1)
http://www.wolframalpha.com/input/?i=%2...
Takšna je funkcija ? http://www.wolframalpha.com/input/?i=%2...
2/3 lahko prepišemo, ker je (c*f(x))' = c*f'(x)
koren pretvoriš v potenco 1/2 in daš exsponenta na skupni imenovalec 3/2 torej, nato pa odvajaš in dobiš 3/2 * x^ (3/2 -1)
http://www.wolframalpha.com/input/?i=%2...
Korak naprej ni vedno ustrezen...sploh če si na robu prepada!
darkolord ::
Očitno ga moti ulomek v eksponentu.
V vsakem primeru od eksponenta odšteješ 1, ne glede na to, ali je celo število ali ne. Če 3/2, od tega isto odšteješ 1 (oz 2/2) in ostane v eksponentu še 1/2.
V vsakem primeru od eksponenta odšteješ 1, ne glede na to, ali je celo število ali ne. Če 3/2, od tega isto odšteješ 1 (oz 2/2) in ostane v eksponentu še 1/2.
teoo ::
mal obrneš pa imaš 2/3*x(3/2)
potem pa osnove odvodov: xy'=y*xy-1
2/3*(3/2* X(3/2 - 2/2)
potem pa osnove odvodov: xy'=y*xy-1
2/3*(3/2* X(3/2 - 2/2)
defying gravity
Mario2 ::
V rešitvah piše da je rešitev koren x! To me moti! Jaz pa do takšnega rezultata nikakor ne morem pridet!
Zgodovina sprememb…
- spremenilo: Mario2 ()
lebdim ::
Veliko bolje je zapisati funkcijo v obliki potence, ker jih lažje odvajaš in tudi integriraš. sqrt(x) = x1/2. To boš tukaj pri odvodih in integralih velikokrat rabil.
lebdim ::
Tega odvajanja bi se pa navsezadnje lahko lotil tudi po pravilu produkta (x*sqrt(x)):
((2/3)*x*sqrt(x))' = (2/3)*(x*sqrt(x))' = (2/3)*[(x)'*sqrt(x) + (x)*(sqrt(x))') = (2/3) * [(1*sqrt(x)) + x*(1/(2*sqrt(x)))] = (2/3) * [sqrt(x) + (x/(2*sqrt(x)))] = (2/3) * ((3x)/(2*sqrt(x))) = (2/3) * ((3x)/(2*sqrt(x))) = x/(sqrt(x)) = sqrt(x)
Ampak opaziš da je precej bolje, če zapišeš funkcijo v obliki potence. Torej f(x) = (2/3)*x*sqrt(x) = (2/3)*x3/2.
Potem samo odvajaš kot f'(x) = (2/3)*(3/2)*x1/2 = x1/2, kar pa je sqrt(x).
((2/3)*x*sqrt(x))' = (2/3)*(x*sqrt(x))' = (2/3)*[(x)'*sqrt(x) + (x)*(sqrt(x))') = (2/3) * [(1*sqrt(x)) + x*(1/(2*sqrt(x)))] = (2/3) * [sqrt(x) + (x/(2*sqrt(x)))] = (2/3) * ((3x)/(2*sqrt(x))) = (2/3) * ((3x)/(2*sqrt(x))) = x/(sqrt(x)) = sqrt(x)
Ampak opaziš da je precej bolje, če zapišeš funkcijo v obliki potence. Torej f(x) = (2/3)*x*sqrt(x) = (2/3)*x3/2.
Potem samo odvajaš kot f'(x) = (2/3)*(3/2)*x1/2 = x1/2, kar pa je sqrt(x).
lebdim ::
Zato, ker je to število in število pri odvodih vedno lahko daš ven.
Primer: Če želiš odvajati f(x) = 2*x2.
f'(x) = (2*x2)' = 2 * (x2)' = 2 * (2x) = 4x
Primer: Če želiš odvajati f(x) = 2*x2.
f'(x) = (2*x2)' = 2 * (x2)' = 2 * (2x) = 4x
Zgodovina sprememb…
- spremenil: lebdim ()

Invictus ::
Zakaj se pri odvajanju ulomek 2/3 ne spremeni v nič. Ampak ostane?
Odvod konstante je 0.
Če ne veš od kje, se nauči od kje odvod sploh izhaja ...
"Life is hard; it's even harder when you're stupid."
http://goo.gl/2YuS2x
http://goo.gl/2YuS2x
lebdim ::
definicija odvoda - lepo vse razloženo ...
vse o odvodih - lepo vse razloženo ...
Pa prosim Mario2, uči se z razumevanjem. Preglej malo te videe.
vse o odvodih - lepo vse razloženo ...
Pa prosim Mario2, uči se z razumevanjem. Preglej malo te videe.
Zgodovina sprememb…
- spremenil: lebdim ()
Yacked2 ::
Zakaj se pri odvajanju ulomek 2/3 ne spremeni v nič. Ampak ostane?
Odvod konstante je 0.
Če ne veš od kje, se nauči od kje odvod sploh izhaja ...
Jap, ampak tole morš odvajat kot produkt: (C * f(x))' = C* f'(x)
Korak naprej ni vedno ustrezen...sploh če si na robu prepada!

Invictus ::
Jap, ampak tole morš odvajat kot produkt: (C * f(x))' = C* f'(x)
Sam tole kar si napisal, ni konstanta ...
"Life is hard; it's even harder when you're stupid."
http://goo.gl/2YuS2x
http://goo.gl/2YuS2x
Yacked2 ::
Jap, ampak tole morš odvajat kot produkt: (C * f(x))' = C* f'(x)
Sam tole kar si napisal, ni konstanta ...
produkt konstante in funkcije, ravno to kar moti OPja
Korak naprej ni vedno ustrezen...sploh če si na robu prepada!
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Matematika kompozitum funkcijOddelek: Šola | 2745 (2510) | lebdim |
| » | Matematika-odvodiOddelek: Šola | 1243 (1000) | kor11 |
| » | integralOddelek: Šola | 3626 (2063) | Elyon8472 |
| » | Matematika - pomoč (strani: 1 2 3 )Oddelek: Šola | 29908 (26483) | daisy22 |
| » | LimitiranjeOddelek: Znanost in tehnologija | 3378 (2568) | CHAOS |