Forum » Šola » Opisna geometrija - težave
Opisna geometrija - težave
gregor4f ::
Pozdravljeni!
Imam problem z reševanjem nalog pri opisni geometriji. Zaradi prehitrega predavanje žal ne zaznam vseh napotkov zato vas naprošam, če mi prosim razložite potek in dodate kakšno skico za tile dve nalogi. Lahko samo v mongeovi metodi, dalje bom že znal. Hvala že v naprej!
1.
Narišite po metodi prirejenih normalnih projekcij (Mongeovi metodi) in v predpisani vojaški
aksonometriji iz izbrane točke Q(x,y,z) ravnine E padnice g1, g2 in g3 (ki so tudi premice!), če je
ravnina E podana za posamezne skupine:
I. – s sečnicama p(P(x,y,z)S(x,y,z)) in r(R(x,y,z)S);
II. – s točko T(x,y,z) in premico p(P(x,y,z)R(x,y,z));
III. – s tremi točkami ABC(A(x,y,z)B(x,y,z)C(x,y,z));
IV. – z vzporednicama a(A(x,y,z)C(x,y,z)) in b(B(x,y,z));
Pozor! Slednice in padnice obvezno določi s sledišči (ki so označene točke)! Odebeli samo
premice, ki sodijo k podatkom ali rezultatu!
1 list formata A4. Dve risbi.
MOJI PODATKI:
p(P(1/2 ,2, 5/2) R(4 ,1/2, 1)) T(3, 3/2, 1;) Q(2, 5/2, ?)
2.
Narišite po metodi prirejenih normalnih projekcij (Mongeovi metodi) in v predpisani vojaški
aksonometriji iz izbrane točke Q(x,y,z) ravnine E normalo n (ki je tudi premica!), če je ravnina E
podana za posamezne skupine:
I. – s točko T(x,y,z) in premico p(P(x,y,z)R(x,y,z));
II. – s tremi točkami ABC(A(x,y,z)B(x,y,z)C(x,y,z));
III. – z vzporednicama a(A(x,y,z)C(x,y,z)) in b(B(x,y,z));
IV. – s sečnicama p(P(x,y,z)S(x,y,z)) in r(R(x,y,z)S);
Pozor! Slednice in normalo obvezno določi s sledišči (ki so označene točke)! Odebeli samo
premice, ki sodijo k podatkom ali rezultatu!
1 list formata A4. Dve risbi.
MOJI PODATKI:
ABC(A(1/2, 3, 5/2) B(4, 1/2, 1) C(5/2, 5/2, 1/2); Q(2, 1, ?)
Imam problem z reševanjem nalog pri opisni geometriji. Zaradi prehitrega predavanje žal ne zaznam vseh napotkov zato vas naprošam, če mi prosim razložite potek in dodate kakšno skico za tile dve nalogi. Lahko samo v mongeovi metodi, dalje bom že znal. Hvala že v naprej!
1.
Narišite po metodi prirejenih normalnih projekcij (Mongeovi metodi) in v predpisani vojaški
aksonometriji iz izbrane točke Q(x,y,z) ravnine E padnice g1, g2 in g3 (ki so tudi premice!), če je
ravnina E podana za posamezne skupine:
I. – s sečnicama p(P(x,y,z)S(x,y,z)) in r(R(x,y,z)S);
II. – s točko T(x,y,z) in premico p(P(x,y,z)R(x,y,z));
III. – s tremi točkami ABC(A(x,y,z)B(x,y,z)C(x,y,z));
IV. – z vzporednicama a(A(x,y,z)C(x,y,z)) in b(B(x,y,z));
Pozor! Slednice in padnice obvezno določi s sledišči (ki so označene točke)! Odebeli samo
premice, ki sodijo k podatkom ali rezultatu!
1 list formata A4. Dve risbi.
MOJI PODATKI:
p(P(1/2 ,2, 5/2) R(4 ,1/2, 1)) T(3, 3/2, 1;) Q(2, 5/2, ?)
2.
Narišite po metodi prirejenih normalnih projekcij (Mongeovi metodi) in v predpisani vojaški
aksonometriji iz izbrane točke Q(x,y,z) ravnine E normalo n (ki je tudi premica!), če je ravnina E
podana za posamezne skupine:
I. – s točko T(x,y,z) in premico p(P(x,y,z)R(x,y,z));
II. – s tremi točkami ABC(A(x,y,z)B(x,y,z)C(x,y,z));
III. – z vzporednicama a(A(x,y,z)C(x,y,z)) in b(B(x,y,z));
IV. – s sečnicama p(P(x,y,z)S(x,y,z)) in r(R(x,y,z)S);
Pozor! Slednice in normalo obvezno določi s sledišči (ki so označene točke)! Odebeli samo
premice, ki sodijo k podatkom ali rezultatu!
1 list formata A4. Dve risbi.
MOJI PODATKI:
ABC(A(1/2, 3, 5/2) B(4, 1/2, 1) C(5/2, 5/2, 1/2); Q(2, 1, ?)
TeaGETREAL ::
Zdravo!
Vem, da je ta objava že stara, ampak zavoljo vseh bodočih arhitektov, ki se boste še s tem ukvarjali bom napisala rešitve za te naloge.
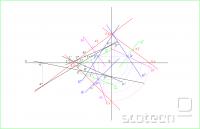
prva vaja - padnice:
Najprej narišem podatke, ki mi bodo pomagali določiti slednice ravnine. To so v tvojem primeru točka T in premica p, ki je določena z dvema točkama P in R. Ko so podatki izrisani, povežem točko T z eno od točk, ki določajo premico p (v mojem primeru z točko P). Sedaj, ko imamo dve premici, ki določata ravnino, ki jo iščemo, poiščemo točke, kjer ti dve premici v tlorisu in v narisu sekata os x. Dobljene točke (v mojem primeru označene z 1,2,3 in 4) prenesemo na premico v nasprotnem risu - torej točko dobljeno na osi x in premici p' prenesemo na premico p'' in obratno, kot je razvidno na sliki. Nato skupaj povežemo dve dobljeni točki v narisu in skupaj dve dobljeni točki v tlorisu. Dve premici označeni z rdečim sta naši slednici ravnine. S prenosom Ey v tretji ris dobimo še tretjo slednico ravnine.
Sedaj narišem še točko Q, skozi katero mora potekati padnica (modre barve),. Padnica = premica ravnine, ki je prevokotna na slednico, zato skozi Q narišem pravokotnico na slednico e1'. Potem padnico prenesem še v ostale rise in povsod določim točko Q (na sliki so vse označene s Q', ker sem jih pozabila popravit v Q'' in Q'''), tako kot je razvidno iz slike (ponovno določam presečišča z osjo x in jih prenašam na slednico, presečišča s slednico pa na os x). Določiti moram še dve padnici (rožnata in zelena) in jih prenesti v ostale rise.
Naloga končana!
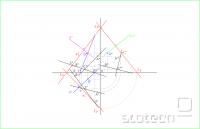
druga vaja - normale:
No, tukaj spet iščemo slednice ravnine, ki je določena v tvojem primeru s tremi točkami. Točke A B in C narišemo in jih povežemo tako, da dobimo dve premici, ki se sekata v točki C. Naprej postopamo tako kot zgoraj. Torej še enkrat poiščemo točke, kjer ti dve premici v tlorisu in v narisu sekata os x. Dobljene točke (v mojem primeru označene z 1,2 in 3 - 4 tokrat nisem risala, ker je predaleč izven lista, sploh pa je slednica že določena s pomočjo točke Ex in točke 3''. Če pa bi radi preverili pravilnost, lahko narišete za lastno vednost še 4ko in pogledate, če se stvar poklapa) prenesemo na premico v nasprotnem risu - torej točko dobljeno na osi x in premici p' prenesemo na premico p'' in obratno, kot je razvidno na sliki. Nato skupaj povežemo dve dobljeni točki v narisu in skupaj dve dobljeni točki v tlorisu. Dve premici označeni z rdečim sta naši slednici ravnine. S prenosom Ey v tretji ris dobimo še tretjo slednico ravnine. V tretji ris prenesemo še točke A B C.
Sedaj narišemo še točko Q. Skozi njo narišemo normalo = premica, ki je pravokotna na ravnino, v našem primeru je to n' (v modri barvi). Zato zopet narišemo pravokotnico na e1'. Poiskati moramo še točko Q v narisu in v tretjem risu. Pomagamo si z normalo - zopet iščemo presečišča z osjo x in slednico, ter jih prenašamo navzgor. Dobimo premico nosilko, na kateri leži točka Q''. Sedaj lahko prenesemo Q še v 3 ris. Da bi vajo dokončali moramo narisati še normalo n''' v tretjem risu skozi Q''' in normalo n'' v narisu skozi Q''.
Naloga končana!
Upam, da bo komu v pomoč.
Vem, da je ta objava že stara, ampak zavoljo vseh bodočih arhitektov, ki se boste še s tem ukvarjali bom napisala rešitve za te naloge.
prva vaja - padnice:
Najprej narišem podatke, ki mi bodo pomagali določiti slednice ravnine. To so v tvojem primeru točka T in premica p, ki je določena z dvema točkama P in R. Ko so podatki izrisani, povežem točko T z eno od točk, ki določajo premico p (v mojem primeru z točko P). Sedaj, ko imamo dve premici, ki določata ravnino, ki jo iščemo, poiščemo točke, kjer ti dve premici v tlorisu in v narisu sekata os x. Dobljene točke (v mojem primeru označene z 1,2,3 in 4) prenesemo na premico v nasprotnem risu - torej točko dobljeno na osi x in premici p' prenesemo na premico p'' in obratno, kot je razvidno na sliki. Nato skupaj povežemo dve dobljeni točki v narisu in skupaj dve dobljeni točki v tlorisu. Dve premici označeni z rdečim sta naši slednici ravnine. S prenosom Ey v tretji ris dobimo še tretjo slednico ravnine.
Sedaj narišem še točko Q, skozi katero mora potekati padnica (modre barve),. Padnica = premica ravnine, ki je prevokotna na slednico, zato skozi Q narišem pravokotnico na slednico e1'. Potem padnico prenesem še v ostale rise in povsod določim točko Q (na sliki so vse označene s Q', ker sem jih pozabila popravit v Q'' in Q'''), tako kot je razvidno iz slike (ponovno določam presečišča z osjo x in jih prenašam na slednico, presečišča s slednico pa na os x). Določiti moram še dve padnici (rožnata in zelena) in jih prenesti v ostale rise.
Naloga končana!
druga vaja - normale:
No, tukaj spet iščemo slednice ravnine, ki je določena v tvojem primeru s tremi točkami. Točke A B in C narišemo in jih povežemo tako, da dobimo dve premici, ki se sekata v točki C. Naprej postopamo tako kot zgoraj. Torej še enkrat poiščemo točke, kjer ti dve premici v tlorisu in v narisu sekata os x. Dobljene točke (v mojem primeru označene z 1,2 in 3 - 4 tokrat nisem risala, ker je predaleč izven lista, sploh pa je slednica že določena s pomočjo točke Ex in točke 3''. Če pa bi radi preverili pravilnost, lahko narišete za lastno vednost še 4ko in pogledate, če se stvar poklapa) prenesemo na premico v nasprotnem risu - torej točko dobljeno na osi x in premici p' prenesemo na premico p'' in obratno, kot je razvidno na sliki. Nato skupaj povežemo dve dobljeni točki v narisu in skupaj dve dobljeni točki v tlorisu. Dve premici označeni z rdečim sta naši slednici ravnine. S prenosom Ey v tretji ris dobimo še tretjo slednico ravnine. V tretji ris prenesemo še točke A B C.
Sedaj narišemo še točko Q. Skozi njo narišemo normalo = premica, ki je pravokotna na ravnino, v našem primeru je to n' (v modri barvi). Zato zopet narišemo pravokotnico na e1'. Poiskati moramo še točko Q v narisu in v tretjem risu. Pomagamo si z normalo - zopet iščemo presečišča z osjo x in slednico, ter jih prenašamo navzgor. Dobimo premico nosilko, na kateri leži točka Q''. Sedaj lahko prenesemo Q še v 3 ris. Da bi vajo dokončali moramo narisati še normalo n''' v tretjem risu skozi Q''' in normalo n'' v narisu skozi Q''.
Naloga končana!
Upam, da bo komu v pomoč.
Zgodovina sprememb…
- zavaroval slike: bluefish ()
TeaGETREAL ::
No, to se večina študentov arhitekture sprašuje in po moje je brez veze, da zdaj tukaj še mi polemiziramo. To se pač zahteva v 1. letniku in treba je stvar prej ali slej opravit, če hočeš diplomirat.
Ampak, da potešim tvojo radovednost - to je nekakšen okrneli ostanek iz časov, ko se na arhitekturi ni uporabljalo računalnikov. Ko je bilo treba na roke (in seveda točno) narisat 3d predstavitev za naročnika (kar pač danes v izi naredimo z modeliranjem in renderiranjem), je še kako prav prišlo znanje opisne geometrije in sicer za risanje senc - senčenje objektov, kar je dalo stvari bolj realen izgled - prostorsko predstavo.
V zgornji vaji sicer še ni nobenega senčenja, ker so to začetne vaje iz prvega semestra, ki nekako predstavijo študentu neuporabni svet opisne geometrije, ga spoznajo z osnovnimi pojmi (padnica, normala, slednica, soslednica,..) in osnovnimi postopki (vrtenje oz zvračanje, projiciranje na stranske ravnine,...), zato da potem v poletnem semestru lahko veselo riše sence zapletenih objektov.
A bo v redu?
Ampak, da potešim tvojo radovednost - to je nekakšen okrneli ostanek iz časov, ko se na arhitekturi ni uporabljalo računalnikov. Ko je bilo treba na roke (in seveda točno) narisat 3d predstavitev za naročnika (kar pač danes v izi naredimo z modeliranjem in renderiranjem), je še kako prav prišlo znanje opisne geometrije in sicer za risanje senc - senčenje objektov, kar je dalo stvari bolj realen izgled - prostorsko predstavo.
V zgornji vaji sicer še ni nobenega senčenja, ker so to začetne vaje iz prvega semestra, ki nekako predstavijo študentu neuporabni svet opisne geometrije, ga spoznajo z osnovnimi pojmi (padnica, normala, slednica, soslednica,..) in osnovnimi postopki (vrtenje oz zvračanje, projiciranje na stranske ravnine,...), zato da potem v poletnem semestru lahko veselo riše sence zapletenih objektov.
A bo v redu?
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Matematika-problemOddelek: Šola | 1900 (1674) | Math Freak |
| » | Ravnine v prostoruOddelek: Šola | 2200 (2111) | alro |
| » | VektorjiOddelek: Šola | 3582 (3290) | lebdim |
| » | Matematična težavaOddelek: Šola | 9795 (9586) | bosstjann |
| » | pomoč pri linearni algebriOddelek: Šola | 3624 (3475) | whatever |