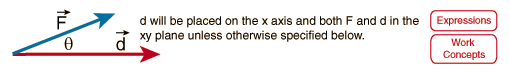Forum » Šola » skalarni, vektorski in ostali produkti
skalarni, vektorski in ostali produkti
Tim Burton ::
Bolj kot gledam, man mi je jasno. Najprej smo obravnavali produkt vektorja s skalarjem (kar se mi še zdi razumljivo, pač vektor množiš s številom/skalarjem, stvar se skrči/raztegne in konec debate), no potem je bil tu še skalarni produkt (a vektorsko * b vektorsko * cos fi), tle se mi je zdelo da je to pač produkt dveh vektorjev, podobno kot jih seštejemo ali odštejemo. No in moja teorija se je podrla ko sem prišel do vektorskega produkta dveh vektorjev no kasneje bom nabasal še na mešani produkt treh vektorjev.
No in zdej problem, v vsej tej poplavi sem ratal zmeden in mi ni več jasno kaj je kaj in zakaj je to tako. Mi zna kdo razložit po domače (kokr se pač da) kaj so zdej te posamezne zadeve, jst bolj ko tuhtam bolj se zgublam.
No in zdej problem, v vsej tej poplavi sem ratal zmeden in mi ni več jasno kaj je kaj in zakaj je to tako. Mi zna kdo razložit po domače (kokr se pač da) kaj so zdej te posamezne zadeve, jst bolj ko tuhtam bolj se zgublam.
Bojevnik ::
Vektorski produkt dveh vektorjev naredi nov vektor, ki je pravokoten na oba vektorja. Dolg pa toliko kolikor je ploščina paralelogram prvih dveh voktorjev.
Upam da te je to zanimalo.
Upam da te je to zanimalo.
McHusch ::
V resnici je rezultat vektorskega produkta psevdovektor, ampak za osnovno predstavo bo zadoščalo, da gre za vektor, ki je pravokoten nanju in po velikost številčno enak ploščini paralelograma, ki ga napenjata. Seveda je tu še vprašanje smeri - rezultat gledamo v desnem smislu, zato tudi ne komutira!
Skalarni produkt je število, ki ti pove, kako dolg je en vektor, če ga pravokotno projeciraš na drugega.
Mešani produkt je število, ki ti pove, kakšen volumen ima paralelopiped, ki ga napenjajo trije vektorji.
Tako za predstavo, da me ne bo kakšen matematik za ušesa.
Skalarni produkt je število, ki ti pove, kako dolg je en vektor, če ga pravokotno projeciraš na drugega.
Mešani produkt je število, ki ti pove, kakšen volumen ima paralelopiped, ki ga napenjajo trije vektorji.
Tako za predstavo, da me ne bo kakšen matematik za ušesa.
Tim Burton ::
Se pravi je vektorski produkt zanimiv samo iz stališča ploščine paralelograma? Tole da je pravokoten, ali to slučajn pomen, da se raztegne v tretjo dimenzijo? Drugače si ne znam predstavlat da bi bil pravokoten na oba primarna vektorja? Se pravi če dobiš rezultat vek. produkta recimo 10, to pomen da je paralelogram med dvema vektorjema velik 10 enot^2?
McHusch ::
Tole da je pravokoten, ali to slučajn pomen, da se raztegne v tretjo dimenzijo?
Da.
Se pravi če dobiš rezultat vek. produkta recimo 10, to pomen da je paralelogram med dvema vektorjema velik 10 enot^2?
Da.
gzibret ::
> Se pravi je vektorski produkt zanimiv samo iz stališča ploščine paralelograma?
Ne, zanimiv je tudi takrat, ko moraš poiskati vektor, ki je pravokoten na dva podana vektorja (pri računanju normale ravnine npr.).
Ne, zanimiv je tudi takrat, ko moraš poiskati vektor, ki je pravokoten na dva podana vektorja (pri računanju normale ravnine npr.).
Vse je za neki dobr!
sevencores ::
skalarni produkt pri fiziki....A=F*d*cos(phi) če množiš s cos(phi) dobiš projekcijo vektorja na drugega, to pa pomeni da se upošteva samo komponenta vektorja ki je vzopredna v našem primeru(poti)...vektor je pač stvar ki v sebi nosi informacijo o velikosti količine in smeri...je več kot samo število...torej če boš ti vlekel vozičen poln premoga vzporedno s tlemi boš naredil z manj sile(F*cos(0)) isto delo kot z več sile (F*cos(45))...pri vektorskem produktu je pač tako v naravi da če pomnožiš recimo tokovni element v magnetnem polju bo pač sila pokazala v določeno smer z določeno velikostjo...
snow ::
> Se pravi je vektorski produkt zanimiv samo iz stališča ploščine paralelograma?
Ne, zanimiv je tudi takrat, ko moraš poiskati vektor, ki je pravokoten na dva podana vektorja (pri računanju normale ravnine npr.).
Nekatere fizikalne količine so definirane kot vektorski produkt, recimo navor.
Random mutation plus nonrandom cumulative natural selection - Richard Dawkins
demon#666 ::
Se opravičujem, ker obujam staro temo, a se mi zdi še najbolj primerna za moje vprašanje.
Mislim da bom dobu sive lase od skalarnih produktov
Naloga je sledeča:
Točke A,B,C,D,E in F so oglišča pravilnega šetkotinka s stranico 5 cm. Vektorja CE in DF (oba imata uno puščico zgorj) zapišete kot linearno kombinacijo a=AB (puščice nad črkami..) in b=CD (puščice nad črkami..) ter izračunajte skalarni produkt CE skalarno DF (puščice nad črkami..).
Za pomoč se zahvaljujem
LP
Mislim da bom dobu sive lase od skalarnih produktov
Naloga je sledeča:
Točke A,B,C,D,E in F so oglišča pravilnega šetkotinka s stranico 5 cm. Vektorja CE in DF (oba imata uno puščico zgorj) zapišete kot linearno kombinacijo a=AB (puščice nad črkami..) in b=CD (puščice nad črkami..) ter izračunajte skalarni produkt CE skalarno DF (puščice nad črkami..).
Za pomoč se zahvaljujem
LP
sherman ::
\overrightarrow{CE} = \vec{b} - \vec{a} (napaka se odpravlja)
\overrightarrow{DF} = -\vec{b} - 2\vec{a} (napaka se odpravlja)
Za skalarni produkt CE in DF upostevas da je skalarni produkt distributiven glede na sestevanje vektorjev in komutativen, ter da
je \vec{a}\cdot\vec{b} = -\tfrac{1}{2} (napaka se odpravlja).
\overrightarrow{DF} = -\vec{b} - 2\vec{a} (napaka se odpravlja)
Za skalarni produkt CE in DF upostevas da je skalarni produkt distributiven glede na sestevanje vektorjev in komutativen, ter da
je \vec{a}\cdot\vec{b} = -\tfrac{1}{2} (napaka se odpravlja).
JanK ::
Ce je stranica 5, je \vec{a}\cdot\vec{b} = -\tfrac{1}{2}*5*5 = -12.5 (napaka se odpravlja) ter \vec{a}\cdot\vec{a} = \vec{b}\cdot\vec{b} = 1*5*5 = 25 (napaka se odpravlja).
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | Baza v vektorskem prostoruOddelek: Šola | 2979 (1477) | BivšiUser2 |
| » | Matematika - algebra - pomočOddelek: Šola | 1540 (1060) | BivšiUser2 |
| » | VektorjiOddelek: Šola | 3589 (3297) | lebdim |
| » | Vektorji - pomočOddelek: Šola | 1391 (1312) | Boobiz |
| » | Zasuk vektorjaOddelek: Šola | 888 (822) | c0dehunter |