Forum » Programiranje » Potujoči projektil
Potujoči projektil
StratOS ::
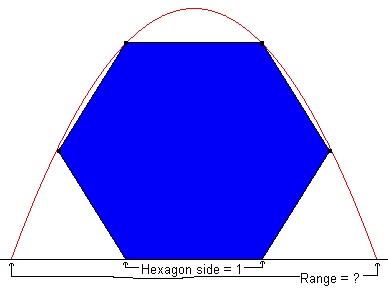
Imamo šestkotnik z stranico dolgo 1, ki leži na ravnih tleh.
Imamo projektil, ki ga postavimo tako, da se mora dotakniti ostalih 4 oglišč šestkotnika, ki ne ležijo na tleh. Na projektil, ki potuje deluje le sila teže.
Vprašanje: Kolikšna je razdalja X (potrebujem na 3 decimalke natančno) je od lokacije starta projektila do konca (padca) projektila.
Slikica za boljšo predstavo je tukaj :
in še namig X < 3
Želel bi videti vaš pristop k temu problemu in mogoče kakšno dobro rešitev.
Imamo projektil, ki ga postavimo tako, da se mora dotakniti ostalih 4 oglišč šestkotnika, ki ne ležijo na tleh. Na projektil, ki potuje deluje le sila teže.
Vprašanje: Kolikšna je razdalja X (potrebujem na 3 decimalke natančno) je od lokacije starta projektila do konca (padca) projektila.
Slikica za boljšo predstavo je tukaj :

in še namig X < 3
Želel bi videti vaš pristop k temu problemu in mogoče kakšno dobro rešitev.
- spremenila: StratOS ()
JerKoJ ::
Naj bi veljajo X=sqrt(7)
Stvar je lepo rešljiva, če veš da projektil leti po paraboli (x^2 osnovna krivulja). Veš za simetričnost te krivulje, vse kar ostane je samo rešitev sistema enačb.
Stvar je lepo rešljiva, če veš da projektil leti po paraboli (x^2 osnovna krivulja). Veš za simetričnost te krivulje, vse kar ostane je samo rešitev sistema enačb.
StratOS ::
Bravo !!
Rešite je možna fizikalno ali matematično
Če vzamemo izhodišče koordinatnega sistema na polovici roba ki leži na tleh dobimo sledeče koordinate ogljišč šestkotnika.
T1(-1,sqrt(3)/2))
T2(-.5, sqrt(3))
T3(0,5,sqrt(3)) i
T4(1,sqrt(3)/2))
pot projektila je kvadratna funkcija ax2+bx+c, pri čem je a<0 in b=0.
Iz sistema dobimo
a=-2*sqrt(3)/3 i
c=7*sqrt(3)/6
iščemo f(x)=0
rešitev za x=+-sqrt(7)/2
končna rešitev: sqrt(7)=2,646.
Rešite je možna fizikalno ali matematično
Če vzamemo izhodišče koordinatnega sistema na polovici roba ki leži na tleh dobimo sledeče koordinate ogljišč šestkotnika.
T1(-1,sqrt(3)/2))
T2(-.5, sqrt(3))
T3(0,5,sqrt(3)) i
T4(1,sqrt(3)/2))
pot projektila je kvadratna funkcija ax2+bx+c, pri čem je a<0 in b=0.
Iz sistema dobimo
a=-2*sqrt(3)/3 i
c=7*sqrt(3)/6
iščemo f(x)=0
rešitev za x=+-sqrt(7)/2
končna rešitev: sqrt(7)=2,646.
Zgodovina sprememb…
- spremenila: StratOS ()
Han ::
Dober si mi ti, StratOS. Ampak, kaj ima to zveze s termodifuzijo? :D Je to kakšna nova grafična metoda reševanja protitočne ekstrakcije? :P
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | EnačbaOddelek: Šola | 1079 (939) | lebdim |
| » | EnačbaOddelek: Šola | 1256 (1061) | lebdim |
| » | Pomoč pri matematiki(čim hitreje)Oddelek: Šola | 1890 (1372) | lebdim |
| » | Kompleksno številoOddelek: Šola | 3232 (2412) | P=LN |
| » | Pomoč pri izračunu matematičnega izraza (koren)Oddelek: Šola | 2923 (2625) | lebdim |