Forum » Problemi človeštva » Global warming
Global warming
Temo vidijo: vsi

jype ::
dni_za_rotacijo=28;
seconds_per_day=dni_za_rotacijo*86400-1;
for (t=0;t<seconds_per_day\2-1;t++) {
It's quite clear to me.
Vsak dan na temle planetu traja 28 zemeljskih dni.
Polovica jih je v temi in tla samo sevajo in se ohlajajo, polovica pa tudi na soncu, in se tla grejejo.
seconds_per_day=dni_za_rotacijo*86400-1;
for (t=0;t<seconds_per_day\2-1;t++) {
It's quite clear to me.
Vsak dan na temle planetu traja 28 zemeljskih dni.
Polovica jih je v temi in tla samo sevajo in se ohlajajo, polovica pa tudi na soncu, in se tla grejejo.
Zgodovina sprememb…
- spremenilo: jype ()
Azrael ::
Nisem noben programer, jure baje je (vsaj takjo se hvali), ampak če prav razumem pripeto kodo, v nastavitvah spremenjivk tega programčka, se lahko nastavi število dni za en obrat planeta (izvorno je 28 dni - Luna?) in algoritem izračuna koliko sekund več ali manj to pomeni v primerjavi z dnevom, ki ima 24 ur.
in še noob vprašanje je ukaz SAY namenjen izpisu na zaslon, nekaj takega kot PRINT v Basicu?
in še noob vprašanje je ukaz SAY namenjen izpisu na zaslon, nekaj takega kot PRINT v Basicu?
Nekoč je bil Slo-tech.
Lonsarg ::
Tako je, jypu očitno ni jasno da je dni_za_rotacijo parameter, ne pa fiksna številka. Čisto lep programčič je tole.

jype ::
Meni je jasno, da Thomasova trditev:
Thomas> Pokaže, da 28 kratna pospešitev rotacije doda dobrih 50 stopinj.
ni skladna s kodo, ki jo je podal. Koda simulira planet, ki se vrti 28x _počasneje_. Da je 50 stopinj bolj vroč, bi kar verjel.
Thomas> Pokaže, da 28 kratna pospešitev rotacije doda dobrih 50 stopinj.
ni skladna s kodo, ki jo je podal. Koda simulira planet, ki se vrti 28x _počasneje_. Da je 50 stopinj bolj vroč, bi kar verjel.
Lonsarg ::
Ne, trenutna koda, ki jo je napisal Simulira točno zdajšno Luno, ki ima dan dolg 28 dni. Morš pač ta parameter spremeniti, da dobiš še kodo, za ko je dan dolg 1 dan, pa potem obje vržež in primerjaš številki.

jype ::
Točno zdajšnjo luno?
Katerega dela
Thomas> Pokaže, da 28 kratna pospešitev rotacije doda dobrih 50 stopinj.
ne razumeš?
Katerega dela
Thomas> Pokaže, da 28 kratna pospešitev rotacije doda dobrih 50 stopinj.
ne razumeš?
Lonsarg ::
Sam ti pa si pikolovski, pa se gres besedne igre. Koda sama po sebi sploh nic ne pokaze, pravilna uporaba te kode ti pokaze, da se ogreje.
Da ne bom zacel vejih mankajocih pri tebi iskat lol.
Da ne bom zacel vejih mankajocih pri tebi iskat lol.
Thomas ::
Simulacija je narejena tako, da je temperatura od zaćetka 0 K in se potem po pričakovanjih čez dan ogreva, čez dan pa ohlaja. Čez nekaj časa se jutranja in druge temperature stabilizirajo.
Lahko pa bi dali kroglo na 1000 K in potem gledali kako bi se hladila do istih temperatur.
Lahko bi korak zmanjšali iz ene sekunde na eno stotinko in dobili še natančnejši rezultat.
Lahko bi vključili še albedo, variabilen po valovnih dolžinah. Ali pa prevajanje toplote in akumulacija v razlučnih tleh. Itd.
Kar sem zaenkrat hotel ilustrirati je le to, kako "vrtenje pogreje". So pa še drugi momenti, ampak zdej moram it spat. Busy days ahead.
Lahko pa bi dali kroglo na 1000 K in potem gledali kako bi se hladila do istih temperatur.
Lahko bi korak zmanjšali iz ene sekunde na eno stotinko in dobili še natančnejši rezultat.
Lahko bi vključili še albedo, variabilen po valovnih dolžinah. Ali pa prevajanje toplote in akumulacija v razlučnih tleh. Itd.
Kar sem zaenkrat hotel ilustrirati je le to, kako "vrtenje pogreje". So pa še drugi momenti, ampak zdej moram it spat. Busy days ahead.
Man muss immer generalisieren - Carl Jacobi
Azrael ::
Programček sem predelal v toliko da dela na MS Qbasic in Free Basic.
Zaenkrat, kaže, da stvar štima, hitreje se planet suče, toplejši je.
Res pa je programček v trenutni fazi prijazen kot kak Linux etc, se pravi treba točno vedeti kaj kateri parameter pomeni in kako vpliva na druge.
Tako leto (year spremenjivka) = časovni okvir, dolgo 3 dni ob dnevu, ki je 3x daljši od normalnega 24 urnega, je povsem enako kot 9 dni po 24 ur.
Ker nisem programer in sem ga lahko kje pokronal, pripenjam kodo (QBasic ne dovoli znaka _ v imenih spremenjivk, zato so imena spremenjivk taka kot so, težko berljiva):
Zaenkrat, kaže, da stvar štima, hitreje se planet suče, toplejši je.
Res pa je programček v trenutni fazi prijazen kot kak Linux etc, se pravi treba točno vedeti kaj kateri parameter pomeni in kako vpliva na druge.
Tako leto (year spremenjivka) = časovni okvir, dolgo 3 dni ob dnevu, ki je 3x daljši od normalnega 24 urnega, je povsem enako kot 9 dni po 24 ur.
Ker nisem programer in sem ga lahko kje pokronal, pripenjam kodo (QBasic ne dovoli znaka _ v imenih spremenjivk, zato so imena spremenjivk taka kot so, težko berljiva):
dnizarotacijo = 1
pi = 3.1415928#
secondsperday = dnizarotacijo * 86400 - 1
specificnatoplotatal = 4200
masatalnakvadratnimeter = 100
omega = 2 * pi / secondsperday
Stefanovakonstanta = 5.67 * 10 ^ -8
year = 9'65
Solarnakonstanta = 1370
average = 0
FOR n = 1 TO year
PRINT n
FOR t = 0 TO secondsperday \ 2 - 1
IF INT((t / 3600) + .5) = t / 3600 THEN PRINT (t \ 3600) + 1; joules; temp; seva
joules = joules + COS(t * omega - pi / 2) * 1300
temp = joules / (specificnatoplotatal * masatalnakvadratnimeter)
average = average + temp
seva = temp ^ 4 * Stefanovakonstanta
joules = joules - seva
NEXT t
FOR t = secondsperday \ 2 TO secondsperday
IF INT((t / 3600) + .5) = t / 3600 THEN PRINT (t \ 3600) + 1; joules; temp; seva
temp = joules / (specificnatoplotatal * masatalnakvadratnimeter)
average = average + temp
seva = temp ^ 4 * Stefanovakonstanta
joules = joules - seva
NEXT t
average = average / secondsperday
NEXT n
PRINT average; " K after"; year; " days"
Nekoč je bil Slo-tech.

jype ::
Thomas> Kar sem zaenkrat hotel ilustrirati je le to, kako "vrtenje pogreje". So pa še drugi momenti, ampak zdej moram it spat. Busy days ahead.
Razumem, da ne boš utegnil, a vseeno imam eno vprašanje.
Če tvoj planet ustavimo (in gledamo planet, ki se glede na izvor energije ne vrti), model izračuna veliko večjo razliko med prejeto in oddano energijo (sum(joules) - sum(seva) za obdobje od prižiga sonca do tam kjer se ustvari ravnovesje) kot pri planetu, ki se vrti (kakorkoli hitro že).
Čemu ostane v planetu več energije, če praviš, da so vrteči se hladnejši?
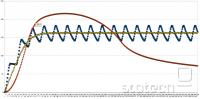
Sicer relacija zgleda ok (prvih 400 ur: rumen se obrne 20x na dan, oranžen enkrat na 20 dni, moder pa 1x na dan:
Razumem, da ne boš utegnil, a vseeno imam eno vprašanje.
Če tvoj planet ustavimo (in gledamo planet, ki se glede na izvor energije ne vrti), model izračuna veliko večjo razliko med prejeto in oddano energijo (sum(joules) - sum(seva) za obdobje od prižiga sonca do tam kjer se ustvari ravnovesje) kot pri planetu, ki se vrti (kakorkoli hitro že).
Čemu ostane v planetu več energije, če praviš, da so vrteči se hladnejši?
Sicer relacija zgleda ok (prvih 400 ur: rumen se obrne 20x na dan, oranžen enkrat na 20 dni, moder pa 1x na dan:
Zgodovina sprememb…
- spremenilo: jype ()
Thomas ::
Čemu ostane v planetu več energije, če praviš, da so vrteči se hladnejši?
Pravim, da vrteči so toplejši.
Man muss immer generalisieren - Carl Jacobi

jype ::
Lapsus ob zgodnjih jutranjih urah. Ne morejo biti toplejši in v sebi zadrževati manj energije.
Lonsarg ::
A lahko malo pojasniš kako si sum(joules) izračunal? Ker joules spremeljivka je uporabljena za trenutno toploto, ne pa prejeto. Me zanima, če si res samo prejeto seštel.

jype ::
incoming += sin(t*omega)*solarna_konstanta*(1-albedo);
joules se potem zmanjša za izsevano, tale pa ne.
seva=2*emisivnost*pow(temp, 4)*stefanova;
outgoing += seva;
joules -= seva;
Ob koncu "dneva" imaš razliko med prejeto in oddano toploto, ki je (kot se iz grafa zgoraj vidi) pozitivna, dokler ne pride do ravnovesja.
joules se potem zmanjša za izsevano, tale pa ne.
seva=2*emisivnost*pow(temp, 4)*stefanova;
outgoing += seva;
joules -= seva;
Ob koncu "dneva" imaš razliko med prejeto in oddano toploto, ki je (kot se iz grafa zgoraj vidi) pozitivna, dokler ne pride do ravnovesja.
Lonsarg ::
Hm seva si dal, kot da cel dan isto seva, a si se samo nerodno izjasnil ali dejansko si tko izračunal? Namreč moral bi v obe zanki dodati števca za seva in v prvo zanko dodati tvoj incoming +=, si naredil tako?
Navpična OS v tvojem grafu pa pomeni trenutno toploto, imam prav?
Navpična OS v tvojem grafu pa pomeni trenutno toploto, imam prav?
Lonsarg ::
Kakšnih K? Saj temperatura je različna na obeh straneh, povprečna temperatura je torej navpična? Torej lahko rečemo da je toplota navpična, saj je toplota premosorazmerna z povprečno temperaturo.

jype ::
Premo? Nikakor ne :)
Ko končam z delom lahko narišem še graf v Joulih - tisto pa je "linearno".
Ko končam z delom lahko narišem še graf v Joulih - tisto pa je "linearno".

jype ::
Ne, Thomasovega.
Moj še ni, ker pri idealni krogli upošteva vse in računa z vsem, tudi atmosfero.
Moj še ni, ker pri idealni krogli upošteva vse in računa z vsem, tudi atmosfero.
imagodei ::
No, ampak tista reč tamle kaže, da ne glede na hitrost vrtenja "povprečna temperatura" ostaja glih?
- Hoc est qui sumus -

jype ::
imagodei> No, ampak tista reč tamle kaže, da ne glede na hitrost vrtenja "povprečna temperatura" ostaja glih?
Morda na prvi pogled. V resnici se planet hitreje segreva, kot se ohlaja, zato "temna stran" ne odda vse toplote, ki jo topla sprejme, razen ko se planet vrti zelo zelo hitro.
Rezultat je ta, da graf nikoli ne potone nazaj do ničle, tudi za zelo počasi vrteče se planete ne.
Morda na prvi pogled. V resnici se planet hitreje segreva, kot se ohlaja, zato "temna stran" ne odda vse toplote, ki jo topla sprejme, razen ko se planet vrti zelo zelo hitro.
Rezultat je ta, da graf nikoli ne potone nazaj do ničle, tudi za zelo počasi vrteče se planete ne.
Lonsarg ::
Ja samo ravno oranžna je počasi rotirajoč in ima nižje črto v povprečju, torej je oranžen bolj hladen, jaz ne vidim kako ta graf tebi v prid govori.

jype ::
Mi ne govori v prid in se strinjam s Thomasom, da po tem modelu zagotovo drži, da vrtenje greje.
Kar me pa čudi je to, da če vrtenje popolnoma ustaviš, se ravnotežje vzpostavi šele po bistveno večji absorbirani energiji, kot sicer. Počasi vrteči imajo manj energije, stoječi pa več. Moral bi narisat graf zadrževane energije v odvisnosti od hitrosti vrtenja, pa je preveč dela za danes.
Kar me pa čudi je to, da če vrtenje popolnoma ustaviš, se ravnotežje vzpostavi šele po bistveno večji absorbirani energiji, kot sicer. Počasi vrteči imajo manj energije, stoječi pa več. Moral bi narisat graf zadrževane energije v odvisnosti od hitrosti vrtenja, pa je preveč dela za danes.
imagodei ::
Kaj pa, če bi v model dodali še kakšno "plast" grude pod površjem. Ali pa več plasti?
A to preveč zakomplicira model?
Bi tud sam naredil, ampak pošteno povem, da mi fizika odpove na tem nivoju.
A to preveč zakomplicira model?
Bi tud sam naredil, ampak pošteno povem, da mi fizika odpove na tem nivoju.
- Hoc est qui sumus -

jype ::
To (gruda spodaj) nič ne vpliva na temperaturo površja, vpliva samo na to, koliko energije je skladiščene v planetu.
Na temperaturo površja vplivajo albedo, emisivnost in potencialno še atmosfera, ki jo trenutno še zanemarjamo. Za atmosfero se celo Thomas strinja, da nosi toploto na mrzlo stran :)
Na temperaturo površja vplivajo albedo, emisivnost in potencialno še atmosfera, ki jo trenutno še zanemarjamo. Za atmosfero se celo Thomas strinja, da nosi toploto na mrzlo stran :)
imagodei ::
Ja saj, a nas ne zanima konec koncev celotna temperatura planeta? In kako na to vpliva vskladiščena temperatura tako tal, kot atmosfere? OK, če atmosfero zanemarimo, pa nekako ne vidim pointa, da se pretvarjamo, da so tla infinitezimalno tanka. Ko se tla na temni strani vrtečega se planeta ohlajajo, prehaja na površino tudi toplota, ki se je uskladiščila preko dneva 1m in 5m globoko... Al si narobe predstavljam?
(Temperatura površja je sicer ena taka smešna zadeva. Če lebdiš 1,5 m nad tlemi na Luni na sončni strani v belem skafandru, ti ne bo nič kaj vroče. Če pa se dotikaš tal, te bo "prijetno" grelo v noge. Če ima planet še atmosfero, se pravila igre nekoliko spremenijo.)
(Temperatura površja je sicer ena taka smešna zadeva. Če lebdiš 1,5 m nad tlemi na Luni na sončni strani v belem skafandru, ti ne bo nič kaj vroče. Če pa se dotikaš tal, te bo "prijetno" grelo v noge. Če ima planet še atmosfero, se pravila igre nekoliko spremenijo.)
- Hoc est qui sumus -

jype ::
imagodei> Ja saj, a nas ne zanima konec koncev celotna temperatura planeta?
Ne vem, predvidevam, da ja :)
imagodei> OK, če atmosfero zanemarimo, pa nekako ne vidim pointa, da se pretvarjamo, da so tla infinitezimalno tanka. Ko se tla na temni strani vrtečega se planeta ohlajajo, prehaja na površino tudi toplota, ki se je uskladiščila preko dneva 1m in 5m globoko... Al si narobe predstavljam?
Prav si predstavljaš, ampak fiziki to lahko zanemarimo :)
Ne vem, predvidevam, da ja :)
imagodei> OK, če atmosfero zanemarimo, pa nekako ne vidim pointa, da se pretvarjamo, da so tla infinitezimalno tanka. Ko se tla na temni strani vrtečega se planeta ohlajajo, prehaja na površino tudi toplota, ki se je uskladiščila preko dneva 1m in 5m globoko... Al si narobe predstavljam?
Prav si predstavljaš, ampak fiziki to lahko zanemarimo :)
Lonsarg ::
Ejjjj jype našel sem kaj je narobe, prej se mi ni dalo natančno analizirati simulacije. Thomasov model velja samo za hitro rotirajoče planete, torej za rpimerjanje Luna in Zemlje je čisto primeren recimo. Namreč model definira dan, kot obrnjenost proti Soncu, noč pa obrnjenost stran od Sonca, in predvidi, da je v enem dnevu ena stran pol časa obrnjena proti Soncu, pol pa stran.
Torej, če bi hotel, da velja tudi za primere, ko je nista obe strani, enako obrnjeni proti soncu, bi rabil spremeniti tisti dve zanki. In to kar konkretno, se sploh ne da na preprost način to simulacijo zdaj spremeniti, da lahko tudi počasneje rotirajočeplanete notri daš.
Oziroma tudi za dokaj počasne velja, pogoj je samo, da se v enem letu vsaj enkrat v celoti zamenjata sončna in senčna stran planeta. Torej simulacija velja, do minimalne dolžine dneva polovico leta.
Torej, če bi hotel, da velja tudi za primere, ko je nista obe strani, enako obrnjeni proti soncu, bi rabil spremeniti tisti dve zanki. In to kar konkretno, se sploh ne da na preprost način to simulacijo zdaj spremeniti, da lahko tudi počasneje rotirajočeplanete notri daš.
Oziroma tudi za dokaj počasne velja, pogoj je samo, da se v enem letu vsaj enkrat v celoti zamenjata sončna in senčna stran planeta. Torej simulacija velja, do minimalne dolžine dneva polovico leta.
Zgodovina sprememb…
- spremenil: Lonsarg ()

jype ::
What?
Ne, za stoječe enostavno drugo zanko odstraniš in prvo podaljšaš na cel dan in meriš power input, iz tega računaš temperaturo, iz temperature power output, in potem integriraš po celi polkrogli. Trivialno, če je pod zemljo res izolator.
Če ni, potem pa seva tudi temna stran planeta, prej ali slej :)
Ne, za stoječe enostavno drugo zanko odstraniš in prvo podaljšaš na cel dan in meriš power input, iz tega računaš temperaturo, iz temperature power output, in potem integriraš po celi polkrogli. Trivialno, če je pod zemljo res izolator.
Če ni, potem pa seva tudi temna stran planeta, prej ali slej :)
Lonsarg ::
Aha no tko si spremenil simulacijo, da si odstranil zanko.
ja moraš potem nekaj vedeti. Thomasova simulacija opazuje samo eno polovico poloble, to razbereš ven iz simulacije? Namrep v prvi zanki opazuje, ko je ta polovica na sončni strani, v drugi, pa ko je ta polovica na enčni strani.
Torej lahko res tako nardiš, da odstraniš drugo zanko za zalockan planet in dobiš ven res toploto imput-output za to polovico, ta druga polovica je pa itak mrzla.
Ampak ko primerjaš z rotirajočim planetom, moraš pa tam pomnožit z dve ta output, ker simulacija meri samo na eni polovici, druga pa je enaka, na hitro rotirajoči.
Še vedno pride zalockan planet bolj topel, če rotirajočemu podvojih akumulirano toploto?
ja moraš potem nekaj vedeti. Thomasova simulacija opazuje samo eno polovico poloble, to razbereš ven iz simulacije? Namrep v prvi zanki opazuje, ko je ta polovica na sončni strani, v drugi, pa ko je ta polovica na enčni strani.
Torej lahko res tako nardiš, da odstraniš drugo zanko za zalockan planet in dobiš ven res toploto imput-output za to polovico, ta druga polovica je pa itak mrzla.
Ampak ko primerjaš z rotirajočim planetom, moraš pa tam pomnožit z dve ta output, ker simulacija meri samo na eni polovici, druga pa je enaka, na hitro rotirajoči.
Še vedno pride zalockan planet bolj topel, če rotirajočemu podvojih akumulirano toploto?

jype ::
Azgard> moraš pa tam pomnožit z dve ta output
Ja ne! Pri obeh simulacijah itak spremljaš samo kvadratni meter na ekvatorju. Šele ko integriraš po polovici krogle, dobiš isto (ker je druga polovica krogle in druga zanka temna in v obeh primerih ne dodaja nič toplote v planet). Rezultat sem tudi preizkusil, saj mora biti končen input in output v obeh primerih enak (in je, razen napake pri računanju s plavajočo vejico).
No saj zdaj se mi je takoj posvetilo. Vsak "kvadratni meter", če je pod površjem izolator, seva tudi v planet enako kot iz planeta (in torej je output energije na spodnji strani plošče enak kot na zgornji, ker simulacija smatra, da je temperatura enaka). Toplota s spodnje strani se izseva v planet in ne more nikamor drugam, kot eventuelno in v povprečju na kvadratni meter na nasprotni strani planeta. Bi si moral vzet čas in premislit, kako to pravilno upoštevat.
Ja ne! Pri obeh simulacijah itak spremljaš samo kvadratni meter na ekvatorju. Šele ko integriraš po polovici krogle, dobiš isto (ker je druga polovica krogle in druga zanka temna in v obeh primerih ne dodaja nič toplote v planet). Rezultat sem tudi preizkusil, saj mora biti končen input in output v obeh primerih enak (in je, razen napake pri računanju s plavajočo vejico).
No saj zdaj se mi je takoj posvetilo. Vsak "kvadratni meter", če je pod površjem izolator, seva tudi v planet enako kot iz planeta (in torej je output energije na spodnji strani plošče enak kot na zgornji, ker simulacija smatra, da je temperatura enaka). Toplota s spodnje strani se izseva v planet in ne more nikamor drugam, kot eventuelno in v povprečju na kvadratni meter na nasprotni strani planeta. Bi si moral vzet čas in premislit, kako to pravilno upoštevat.
Zgodovina sprememb…
- spremenilo: jype ()
Lonsarg ::
Ja spremljaš kvadratni meter in ga dobiš koliko je topel pri zalockanem in koliko pri hitro rotirajočem.
In potem, če te zanima toplota celega planeta moraš takole gledati. Zalockan planet ima pol manj takih kvadratnih metrov, ki so tako topli kakor si izračunal, saj jih ma vendar pol čisto mrzlih. Se ne strinjaš s tem?
Pač ti si eno zanko ven odrezal, in simulacija ni več enaka, in jo ne moreš več direktno po toploti kvadratnega metra primerjat, ker si z izbrisom te zanke spremenil šteivlo toplih kvadratnih metrov.
In potem, če te zanima toplota celega planeta moraš takole gledati. Zalockan planet ima pol manj takih kvadratnih metrov, ki so tako topli kakor si izračunal, saj jih ma vendar pol čisto mrzlih. Se ne strinjaš s tem?
Pač ti si eno zanko ven odrezal, in simulacija ni več enaka, in jo ne moreš več direktno po toploti kvadratnega metra primerjat, ker si z izbrisom te zanke spremenil šteivlo toplih kvadratnih metrov.
Zgodovina sprememb…
- spremenil: Lonsarg ()

jype ::
Azgard> Zalockan planet ima pol manj takih kvadratnih metrov, ki so tako topli kakor si izračunal, saj jih ma vendar pol čisto mrzlih. Se ne strinjaš s tem?
Ja, integriraš po polovici krogle. To je to. You don't touch the other half. S tem si dobil celoten influx energije.
Vrteč se planet pa ma enak influx. Integriraš po celi krogli tisti kvadratni meter, ki ti ga da simulacija. Pride isto.
Razlika se pa akumulira precej večja na stoječem, kar se meni zdi hecno, glede na to da so pogoji enaki.
Ja, integriraš po polovici krogle. To je to. You don't touch the other half. S tem si dobil celoten influx energije.
Vrteč se planet pa ma enak influx. Integriraš po celi krogli tisti kvadratni meter, ki ti ga da simulacija. Pride isto.
Razlika se pa akumulira precej večja na stoječem, kar se meni zdi hecno, glede na to da so pogoji enaki.
Lonsarg ::
Ja sej je logično, topla polovica akumulira več energije pri zalockanem, kot jo polovica na vrtečem. Ker je skozi obrnjena proti Soncu, ne vem kako si lahko mislil, da bi bilo drugače. pri vrtečem je enkrat ena polovica, enkrat pa druga obrnjena proti Soncu, jasno ena sama polovica manj absorbira, ker ni skozi proti Soncu in polovico časa abrosbira tudi druga polovica.
Simulacija govori sam o eni polovici namreč.
Simulacija govori sam o eni polovici namreč.
Zgodovina sprememb…
- spremenil: Lonsarg ()

jype ::
Azgard> Simulacija govori sam o eni polovici namreč.
Ne, simulacija govori samo o enem kvadratnem metru (al čemurkoli že). Ista enota na stoječem planetu se jasno ne more primerjat, ker je ves čas enako osvetljena, zato pa moraš integrirat po celi osvetljeni polovici krogle po sinusu od vpadnega kota.
Pri uni drugi krogli integriraš po celi krogli, ampak osvetljena je vedno samo polovica, tako da je rezultat (jasno in pričakovano) enak.
Kolk energije hranita cela planeta pa izračunaš tako, da zračunaš po kolikem času temperatura doseže ravnovesje. Pri stoječem planetu delaš pri tem še precejšnjo negativno napako, ker se toplota po površju tudi prevaja na hladnejša mesta.
Ne, simulacija govori samo o enem kvadratnem metru (al čemurkoli že). Ista enota na stoječem planetu se jasno ne more primerjat, ker je ves čas enako osvetljena, zato pa moraš integrirat po celi osvetljeni polovici krogle po sinusu od vpadnega kota.
Pri uni drugi krogli integriraš po celi krogli, ampak osvetljena je vedno samo polovica, tako da je rezultat (jasno in pričakovano) enak.
Kolk energije hranita cela planeta pa izračunaš tako, da zračunaš po kolikem času temperatura doseže ravnovesje. Pri stoječem planetu delaš pri tem še precejšnjo negativno napako, ker se toplota po površju tudi prevaja na hladnejša mesta.
Lonsarg ::
Kolk energije hranita cela planeta pa izračunaš tako, da zračunaš po kolikem času temperatura doseže ravnovesje.
??? Q=mcT, ne pa čas po kateren se vzpostavi ravnovesje.
Zalockan planet pa itak nikoli ne vzpostavi ravnovesja...
Zgodovina sprememb…
- spremenil: Lonsarg ()

jype ::
Kakšen T?
Potem bi moral poznati T vsake točke v planetu in integrirat po tem - tega pa ne veš.
Potem bi moral poznati T vsake točke v planetu in integrirat po tem - tega pa ne veš.
Lonsarg ::
Poenostaviš lejga, da je enakomeren po eni polobli to je vendar point vse približkov, ki se jih gremo 20 strani, drugače ne moreš.

jype ::
Azgard> Poenostaviš lejga, da je enakomeren po eni polobli to je vendar point vse približkov, ki se jih gremo 20 strani, drugače ne moreš.
Nč ni enakomeren, to je narobe. Tudi simulacija tega nikjer ne predvideva.
Nč ni enakomeren, to je narobe. Tudi simulacija tega nikjer ne predvideva.
Lonsarg ::
Simulacija tudi ne računa toplote celga planeta, to si ti sam neko svojo potem šov računat, pa rečeš kao simulacija to pokaže.
Sam si zlo zanimiv, ko ti naredimo dokaz za zalockan proti hitro vrtečem, se greš je pa kako to poenostavno, da zdej kar velja za zmer, ko dokaza ne moreš izpodbiti, zdaj ko imaš simulacijo, pa greš ravno ekstremen primer, za katerega moraš simulacijo spreminjat, da sploh lahko računaš in žal narobe spreminjaš, ker ne razumeš kako moraš, oziroma ne veš kaj ti ta spremenjena toplota pomeni.
Sam si zlo zanimiv, ko ti naredimo dokaz za zalockan proti hitro vrtečem, se greš je pa kako to poenostavno, da zdej kar velja za zmer, ko dokaza ne moreš izpodbiti, zdaj ko imaš simulacijo, pa greš ravno ekstremen primer, za katerega moraš simulacijo spreminjat, da sploh lahko računaš in žal narobe spreminjaš, ker ne razumeš kako moraš, oziroma ne veš kaj ti ta spremenjena toplota pomeni.

jype ::
Zdi se mi, da je s simulacijo, ki tega ne zdrži, nekaj sumljivega narobe.
Tudi sicer težko sprejmem, da simuliramo planet, ki je sestavljen iz zelo tanke plasti vode na nekakšnem perfektnem zrcalu, ampak ko ga že, me nič ne moti, če sodelujem.
Tudi sicer težko sprejmem, da simuliramo planet, ki je sestavljen iz zelo tanke plasti vode na nekakšnem perfektnem zrcalu, ampak ko ga že, me nič ne moti, če sodelujem.
Thomas ::
Simulacija je čist OK. Vsaj dokler je ti ne vzameš v roke in delaš z njo nekaj tajnega. Kažeš samo ene čudne rezultate tega dela.
Opusti trud, jure!
Opusti trud, jure!
Man muss immer generalisieren - Carl Jacobi
Thomas ::
Dej, dej, jure. Posprav ti tele tvoje "konstruktivne" pripombe. Njihova vrednost je negativna.
Zdej vam je le jasno, kako narobe ste imeli, ganimed, JJ, jure in pa mogoče še kdo?
Rotacija je major player pri površinski temperaturi. Vem še eno tako presenetljivost. Oziroma dve. Z njima se ponavadi ne operira in se jih ne omenja, sta pa ravno tako lepi in ravno tako bo kdo zaradi njiju prišel na rob živčnega zloma, ko ju bom povedal.
Ampak najprej da je tole jasno. Prej nič.
Zdej vam je le jasno, kako narobe ste imeli, ganimed, JJ, jure in pa mogoče še kdo?
Rotacija je major player pri površinski temperaturi. Vem še eno tako presenetljivost. Oziroma dve. Z njima se ponavadi ne operira in se jih ne omenja, sta pa ravno tako lepi in ravno tako bo kdo zaradi njiju prišel na rob živčnega zloma, ko ju bom povedal.
Ampak najprej da je tole jasno. Prej nič.
Man muss immer generalisieren - Carl Jacobi

jype ::
Thomas> Rotacija je major player pri površinski temperaturi.
_Tvoja_ simulacija ti pravi, da to ne drži.
_Tvoja_ simulacija ti pravi, da to ne drži.
Thomas ::
MOJA simulacija mi pravi da drži, to vedo vsi razen tebe. Sej to ti je že Azgard razložil.
Sam si zlo zanimiv, ko ti naredimo dokaz za zalockan proti hitro vrtečem, se greš je pa kako to poenostavno, da zdej kar velja za zmer, ko dokaza ne moreš izpodbiti, zdaj ko imaš simulacijo, pa greš ravno ekstremen primer, za katerega moraš simulacijo spreminjat, da sploh lahko računaš in žal narobe spreminjaš, ker ne razumeš kako moraš, oziroma ne veš kaj ti ta spremenjena toplota pomeni.
Man muss immer generalisieren - Carl Jacobi
Lonsarg ::
Jah major player, to je zlo relativno. Major je res, če gledaš en planet v vesolju in primerjaš kako hitro rotira, oziroma bi teoretično lahko rotiral. Ker pa imajo planeti stalno hitrost rotacije sploh NI faktor v spremembah temperature. Pa recimo planet, ki se že hitro vrti, recimo Zemlja, ji z povečvanjam hitrosti rotacije skoraj ne moreš več povečati temperature, par stopinj.
Sam da en jype potem trdi da se zmanša, pa no comment:)
Sam da en jype potem trdi da se zmanša, pa no comment:)
Zgodovina sprememb…
- spremenil: Lonsarg ()

jype ::
Thomas> MOJA simulacija mi pravi da drži, to vedo vsi razen tebe. Sej to ti je že Azgard razložil.
Tvoja simulacija pravi, da se lahko temperatura na zemlji spremeni za celo desetinko stopinje v nekaj milijonih let.
Tvoja simulacija pravi, da se lahko temperatura na zemlji spremeni za celo desetinko stopinje v nekaj milijonih let.