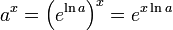Forum » Šola » E (matematična konstanta)
E (matematična konstanta)
euler ::
Kako veš, kje na eksponentnici je točka ki predstavlja e^1 in kje e^0, če nimaš zraven koordinatnega sistema?
Naklon v točki e^0 je 45°, torej pogledaš, v kateri točki je naklon grafa 45°. Naklon v točki e^1 je arctg(e), torej pogledaš, v kateri točki je naklon krivulje tak.
Če pa je graf popačen - raztegnjen (x in y nista sorazmerna, npr. krogi so videti elipse, kvadrati so videti pravokotniki), pa se ne da določiti teh točk, razen če veš, kolikšno je razmerje med polosmi teh elips oziroma pravokotnikov.
Thomas ::
45 stopinj glede na kaj? Saj nimaš nobenega koordinatnega sistema in zato niti ne x osi.
Man muss immer generalisieren - Carl Jacobi
kekz ::
Če imaš možnost pogledati graf od dovolj daleč, lahko določiš os X, ker je asimptota.
Poglej grafe od A.Smith.
Poglej grafe od A.Smith.
euler ::
45° lahko poljubno natančno določimo, če ga odmerimo od tangente na graf e^x v neki zelo oddaljeni točki, npr. e^-1000, saj je tam graf skoraj vodoraven. Na ta način lahko poljubno natančno določimo približek točke e^0.
Ko rišemo tangente v vedno bolj oddaljenih točkah, približki konvergirajo k točki e^0.
Ko rišemo tangente v vedno bolj oddaljenih točkah, približki konvergirajo k točki e^0.
Thomas ::
> e^-1000
Tudi y osi nimaš, zato ne veš, kje je to točka.
Tudi y osi nimaš, zato ne veš, kje je to točka.
Man muss immer generalisieren - Carl Jacobi
euler ::
Lahko pa določiš koordinatni sistem takole:
Denimo, da imaš narisan graf. ZAČETNI KS postaviš bilo kam. Ker veš, da je PRAVI KS zgolj transliran, rotiran in raztegnjen glede na začetnega, je graf glede na začetni KS zgolj transliran, rotiran in raztegnjen graf funkcije e^x. Translacija je za vektor (a,b), rotacija za kot t in razteg za faktor k. Če bi poznal te štiri neznanke, bi lahko začetni KS transliral, rotiral in raztegnil s temi koeficienti in bi dobil pravi KS. Ampak te 4 neznanke lahko preprosto izračunaš z interpolacijo: izbereš si 4 točke na grafu (glede na začetni KS), odčitaš pripadajoče y-e in dobiš 4 enačbe in 4 neznanke - izračunaš a, b, t in k.
Iz postopka je razvidno, da celega grafa sploh ne rabiš, ampak samo 4 točke na grafu. Postopek se lahko uporabi za poljubno funkcijo, ne samo e^x: če je podan graf funkcije in enačba, se da določiti KS. Če pa isti postopek delamo za premico, pa hitro ugotovimo, da enačbe za a, b, t in k niso neodvisne in ima enačba več rešitev, zato se premica razlikuje od e^x.
Ali se komu sanja, o čem sem pisal?
Denimo, da imaš narisan graf. ZAČETNI KS postaviš bilo kam. Ker veš, da je PRAVI KS zgolj transliran, rotiran in raztegnjen glede na začetnega, je graf glede na začetni KS zgolj transliran, rotiran in raztegnjen graf funkcije e^x. Translacija je za vektor (a,b), rotacija za kot t in razteg za faktor k. Če bi poznal te štiri neznanke, bi lahko začetni KS transliral, rotiral in raztegnil s temi koeficienti in bi dobil pravi KS. Ampak te 4 neznanke lahko preprosto izračunaš z interpolacijo: izbereš si 4 točke na grafu (glede na začetni KS), odčitaš pripadajoče y-e in dobiš 4 enačbe in 4 neznanke - izračunaš a, b, t in k.
Iz postopka je razvidno, da celega grafa sploh ne rabiš, ampak samo 4 točke na grafu. Postopek se lahko uporabi za poljubno funkcijo, ne samo e^x: če je podan graf funkcije in enačba, se da določiti KS. Če pa isti postopek delamo za premico, pa hitro ugotovimo, da enačbe za a, b, t in k niso neodvisne in ima enačba več rešitev, zato se premica razlikuje od e^x.
Ali se komu sanja, o čem sem pisal?
euler ::
> y osi nimaš
Greš zelo levo, saj veš, da je tam x približno minus neskončno, ne rabiš y osi. V taki točki odmeriš tangento.
Ampak preberi si "metodo 4 točk" (prejšnji post), ker je zanimiva.
Greš zelo levo, saj veš, da je tam x približno minus neskončno, ne rabiš y osi. V taki točki odmeriš tangento.
Ampak preberi si "metodo 4 točk" (prejšnji post), ker je zanimiva.
kekz ::
Strma je v točki ...
Naklon v točki ...
Tele besedne zveze so mi zanimive in se tudi v praksi veliko uporabljajo.
Če pa pogledamo čisto eksaktno, kako ima lahko karkoli sploh kakšen naklon ali strmino v brezdimenzijskem prostoru (=točki)
Če je neka stvar velika (široka, visoka, globoka) nič, je v resnici bolj težko nagnjena.
Thomas ::
euler,
Nimaš nobenih točk na eksponentnici, ampak samo točke na projekciji eksponentnice na ravnino. Neznanke so tvoj položaj (X,Y,Z), nagnjenost projicirne ravnine na eksponetnico okoli treh kotov. Plus še skala in koordinate izhodišča funkcije.
4 točke zato niso dovolj.
Nimaš nobenih točk na eksponentnici, ampak samo točke na projekciji eksponentnice na ravnino. Neznanke so tvoj položaj (X,Y,Z), nagnjenost projicirne ravnine na eksponetnico okoli treh kotov. Plus še skala in koordinate izhodišča funkcije.
4 točke zato niso dovolj.
Man muss immer generalisieren - Carl Jacobi
euler ::
Jaz si problem predstavljam takole:
Na papirju so narisane 4 točke (ali pa cela krivulja). Nariši KS s primerno skalo, da bo to graf funkcije e^x.
Odkod si tu potegnil 3 dimenzije?
Na papirju so narisane 4 točke (ali pa cela krivulja). Nariši KS s primerno skalo, da bo to graf funkcije e^x.
Odkod si tu potegnil 3 dimenzije?
Thomas ::
Oddaljenost je bila omenjena v mojem prvem postu na to temo. Pa maš 3D.
Man muss immer generalisieren - Carl Jacobi
barbarpapa1 ::
Pozdrav
Če generaliziramo zadevo, da imamo graf ravninske eksponentne funkcije v prostoru (z ravninsko mislim to, da "z" v zapisu funkcije ne nastopa"), potem lahko krožim poljubno okoli funkcije. Torej je v določenem položaju projekcija te funkcije premica. Pravzaprav velja to za vsako krivuljo v ravnini.....
Malo bluzim press...
LP
Jože
Če generaliziramo zadevo, da imamo graf ravninske eksponentne funkcije v prostoru (z ravninsko mislim to, da "z" v zapisu funkcije ne nastopa"), potem lahko krožim poljubno okoli funkcije. Torej je v določenem položaju projekcija te funkcije premica. Pravzaprav velja to za vsako krivuljo v ravnini.....
Malo bluzim press...
LP
Jože
euler ::
Oddaljenost je podana s skalo - bolj ko je skala drobna, večja je oddaljenost. Poleg tega nič nismo rekli, da je "projicirana ravnina" lahko nagnjena, saj potem projicirana skala ni več kvadratna mreža, ampak pravokotna. Veš, kaj mislim?
Thomas ::
Jah ... ne. Maš pač premico v prostoru in njena projekcija na tvojo kamero ali mrežnico (odvisno od tega a si človek ali stroj). Za premico iz podatka na mrežnici (PLUS FORMULE!) ne moreš sklepati kje je. Za eksponentnico pa tudi ne. Za krog pa lahko, koliko krogov daleč je. Tudi če je kaj obrnjen ipd.
Man muss immer generalisieren - Carl Jacobi
euler ::
1. Projekcija npr. na fotoaparatu zelo popači slike. Če s fotoaparatom slikaš nagnjeno premico v prostoru, na sliki ne dobiš premice, ampak neko krivuljo. Skratka take projekcije so zelo zakomplicirane.
Kako to utemeljuješ?
Za eksponentnico pa tudi ne.
Kako to utemeljuješ?
Thomas ::
Lej ... v roku do konca tedna bom napisal vse, kako in zakaj, v enem obširnejšem postu.
Seveda boš dobrodošel, da ga razsuješ po svojih najboljših močeh.
P.S.
Na popačenja nisem mislil, razen seveda na perspektivo. Ta je the fact of life in 3D. Pa ne samo v 3D.
Seveda boš dobrodošel, da ga razsuješ po svojih najboljših močeh.
P.S.
Na popačenja nisem mislil, razen seveda na perspektivo. Ta je the fact of life in 3D. Pa ne samo v 3D.
Man muss immer generalisieren - Carl Jacobi
micromollis ::
Živjo Thomas!
Nočem te priganjat, vendar me vedoželjnost in radovednost sili, da te prosim za obljubljeno sporočilo .
.
Lp
Nočem te priganjat, vendar me vedoželjnost in radovednost sili, da te prosim za obljubljeno sporočilo
Lp
Thomas ::
Sej bo. Samo zdej nekej hudga delam, pa nimam časa. Samo, sej bo kmalu.
Man muss immer generalisieren - Carl Jacobi
euler ::
To, da se e pojavlja v številnih fizikalnih in kemijskih formulah, je ZAVAJAJOČE. Res je sicer, da se številni procesi obnašajo eksponentno, ampak to ne z osnovo e, ampak z eno levo osnovo a. Razlog, da je potem v teh formulah osnova e, tiči v tem, da se da zapisati a^x kot e^(ln(a)*x), potem pa ln(a) proglasimo za novo konstanto k in dobimo e^(kx). V številu e ni nič naravnega (v fizikalno/kemijskem smislu), v formule je vpeljan na silo. Isti štos je pri ln: fiziki in kemiki pridejo do formule log_a(x) (logaritem z osnovo a), ampak to zapišejo kot log_a(x)=ln(x)/ln(a)=k*ln(x), kjer k=1/ln(x). Konstanta e torej NI naravna, prav tako "naravni logaritem" NI naraven - v naravi se ne pojavlja.
V matematiki je e naraven v tem smislu: odvod od e^x je e^x. Ekvivalentno (za eksponentne funkcije): naklon pri x=0 je 45°.
V matematiki je e naraven v tem smislu: odvod od e^x je e^x. Ekvivalentno (za eksponentne funkcije): naklon pri x=0 je 45°.
JanK ::
Thomas ::
No, tale funkcija ki si jo narisal, ni exp(x), pač pa takoimenovana krompirjeva olupnica.
Če bi narisal pa pravo exp(x), skupaj recimo z x osjo, potem bi videl, da y os (in s tem dolžinsko enoto) lahko potegneš kjerkoli, pa vse štima.
Dojel in zapopadel? Naposled.
Če bi narisal pa pravo exp(x), skupaj recimo z x osjo, potem bi videl, da y os (in s tem dolžinsko enoto) lahko potegneš kjerkoli, pa vse štima.
Dojel in zapopadel? Naposled.
Man muss immer generalisieren - Carl Jacobi
redo ::
> Thomas, ali si že slišal za fraktale? To so strukture, ki so videti enake, ne glede na to, kako od blizu jih pogledaš. Premica npr. je fraktal, medtem ko e^x ni.
Kako veš, kje na eksponentnici je točka ki predstavlja e^1 in kje e^0, če nimaš zraven koordinatnega sistema?
Zapis e^1 brez koordinatnega sistema nima pomena.
Vedno lahko definiram koordinatni sistem glede na robove slike, ki je podana.
Jaz sicer ne vem, kaj točno pomeni "videti enake", ampak odvodi funkcije e^x na robovih slike, oziroma kot med tangentama iz točk na robovih, se iz slike v sliko za funkcijo e^x spreminjajo (tako kot npr. za parabolo). Funkcija mora tako na nekaterih slikah delovati bolj zlomljena kot na drugih.
EDIT: Popravil nekaj slovničnih napak in zadnji stavek.
Zgodovina sprememb…
- spremenilo: redo ()
redo ::
To, da se e pojavlja v številnih fizikalnih in kemijskih formulah, je ZAVAJAJOČE. Res je sicer, da se številni procesi obnašajo eksponentno, ampak to ne z osnovo e, ampak z eno levo osnovo a. Razlog, da je potem v teh formulah osnova e, tiči v tem, da se da zapisati a^x kot e^(ln(a)*x), potem pa ln(a) proglasimo za novo konstanto k in dobimo e^(kx).
Ampak v tem je ravno srž. Torej je zapis a^x le puder za e^(k x), ki pa ni kaj drugega, kot navaden razteg funkcije e^x. Ko govoriš o eksponentni naravi procesov, te ponavadi ne zanima, s kakšno osnovo je ta eksponentna funkcija. Itak ponavadi zapišeš eksponent v obliki e^(x/x_0) in ne kot b^x, kjer je b neka čudna konstanta e^(1/x_0) s še bolj čudnimi enotami.
Thomas ::
Bistvo exp(x) funkcije, kakor sem blagovolil omenuti že na začetku je to, da ne veš kje je sečišče x in y osi. Lahko je kjerkoli na x. Kjerkoli.
Bomo pokapiral?
Bomo pokapiral?
Man muss immer generalisieren - Carl Jacobi
rasta ::
Bistvo exp(x) funkcije, kakor sem blagovolil omenuti že na začetku je to, da ne veš kje je sečišče x in y osi. Lahko je kjerkoli na x. Kjerkoli.
To ni res. Razlika kotov med tangentami in abcisami katerega koli ortogonalnega sistema je monotono naraščajoča funkcija (kako je rotiran/transliran/skaliran ta poljubni ortogonalni sistem je nepomembno). Iz razlike kotov lahko preračunaš nazaj originalni xy koordinatni sistem.
euler ::
Thomas:
Če smo v 2D in vodoravnih ali navpičnih raztegov ne dovolimo, potem se že iz 4 točk na grafu da določiti KS.
Če dovoljujemo še razteg v smeri x- in y-osi, potem to seveda ne velja več, kot si že sam ugotovil. Če na primer graf e^x pomakneš za 1 v levo in ga raztegneš v y-smeri s faktorjem 1/e, dobiš spet isti graf. Z drugimi besedami, KS lahko pomakneš za 1 v desno in malo spremeniš skalo na abscisi (natančenje, skalo raztegneš s faktorjem e), pa boš dobil spet graf v drugem KS, ki ti opisuje funkcijo e^x. KS torej ni enolično določen. Ampak z istim argumentom lahko vidimo, da v tem primeru za NOBENO funkcijo a^x ne znamo določiti KS. Razlog je natanko isti kot pri e^x: če pri grafu funkcije a^x (z danim KS) premakneš KS za 1 v desno in raztegneš v y-smeri s faktorjem a, boš spet dobil graf a^x. Torej e^x v tem pogledu ne uživa nikakršnih "privilegijev" v primerjavi z drugimi funkcijami a^x.
Če smo v 3D (kot bi nekateri radi zakomplicirali), potem moramo upoštevati raznorazna popačenja. Seveda se potem zakomplicira. Verjetno se (če dopuščamo tudi rotacije v prostoru, translacije itd.) samo iz grafa v 3D res ne da določiti KS, čeprav bi bil tudi pri teh izjavah malo previden, ker na primer že za premico (za katero je v 2D očitno, da ji ne znamo določiti KS, če dovolimo raztege) vemo, da v 3D postane krivulja z asimptoto in iz tega se (morda) lahko marsikaj naračuna, morda celo enolično določi KS.
Če smo v 2D in vodoravnih ali navpičnih raztegov ne dovolimo, potem se že iz 4 točk na grafu da določiti KS.
Če dovoljujemo še razteg v smeri x- in y-osi, potem to seveda ne velja več, kot si že sam ugotovil. Če na primer graf e^x pomakneš za 1 v levo in ga raztegneš v y-smeri s faktorjem 1/e, dobiš spet isti graf. Z drugimi besedami, KS lahko pomakneš za 1 v desno in malo spremeniš skalo na abscisi (natančenje, skalo raztegneš s faktorjem e), pa boš dobil spet graf v drugem KS, ki ti opisuje funkcijo e^x. KS torej ni enolično določen. Ampak z istim argumentom lahko vidimo, da v tem primeru za NOBENO funkcijo a^x ne znamo določiti KS. Razlog je natanko isti kot pri e^x: če pri grafu funkcije a^x (z danim KS) premakneš KS za 1 v desno in raztegneš v y-smeri s faktorjem a, boš spet dobil graf a^x. Torej e^x v tem pogledu ne uživa nikakršnih "privilegijev" v primerjavi z drugimi funkcijami a^x.
Če smo v 3D (kot bi nekateri radi zakomplicirali), potem moramo upoštevati raznorazna popačenja. Seveda se potem zakomplicira. Verjetno se (če dopuščamo tudi rotacije v prostoru, translacije itd.) samo iz grafa v 3D res ne da določiti KS, čeprav bi bil tudi pri teh izjavah malo previden, ker na primer že za premico (za katero je v 2D očitno, da ji ne znamo določiti KS, če dovolimo raztege) vemo, da v 3D postane krivulja z asimptoto in iz tega se (morda) lahko marsikaj naračuna, morda celo enolično določi KS.
Zgodovina sprememb…
- spremenil: euler ()
euler ::
Ampak v tem je ravno srž. Torej je zapis a^x le puder za e^(k x), ki pa ni kaj drugega, kot navaden razteg funkcije e^x..
Ali je e^(kx) razteg a^x ali obratno? Težko je objektivno reči ...
Ko govoriš o eksponentni naravi procesov, te ponavadi ne zanima, s kakšno osnovo je ta eksponentna funkcija. Itak ponavadi zapišeš eksponent v obliki e^(x/x_0) in ne kot b^x, kjer je b neka čudna konstanta e^(1/x_0) s še bolj čudnimi enotami.
V eksponentu tako ali tako ne sme biti enot, zato bi bilo samo b^x res malo neumno. Ampak k*b^(x/x_0), za recimo b=2, je pa čisto ok.
Če recimo gledaš populacijo bakterij 100 bakterij, ki se podvojijo vsako minuto, potem ti zapis N=100*2^(T/60 s) pove več kot pa formula N=100*e^(0.693 T/60 s).
Thomas ::
No, rasta - tole povej!
Nekdo je izbrisal y os na grafu funkcije exp(x). Jo lahko rekonstruiraš, kje je bila, če imaš samo x os in eksponentnico?
Reši ta problem, če moreš!
Če ne moreš ... tud povej.
Nekdo je izbrisal y os na grafu funkcije exp(x). Jo lahko rekonstruiraš, kje je bila, če imaš samo x os in eksponentnico?
Reši ta problem, če moreš!
Če ne moreš ... tud povej.
Man muss immer generalisieren - Carl Jacobi
rasta ::
Če imaš os x na grafu funkcije exp(x), je naloga precej enostavna. Izmeriš pravokotno razdaljo do x osi poljubne točke (to je y1), ter zračunaš x1 iz enačbe y1 = exp(x1).
rasta ::
Če pa je v igri še skaliranje, funkcija je takrat y = A*exp(k*x), potrebujemo dve točki, določiti pa moramo tudi tangenti na ti dve točki.
Tako dobimo sistem enačb štirih enačb s štirimi neznankami (A, k, x1, x2):
y1 = A*exp(k*x1)
y2 = A*exp(k*x2)
tan(φ1) = A*k*exp(k*x1)
tan(φ2) = A*k*exp(k*x2)
Enačbe so sicer transcendenčne, ampak problem je rešljiv (vsaj numerično).
Tako dobimo sistem enačb štirih enačb s štirimi neznankami (A, k, x1, x2):
y1 = A*exp(k*x1)
y2 = A*exp(k*x2)
tan(φ1) = A*k*exp(k*x1)
tan(φ2) = A*k*exp(k*x2)
Enačbe so sicer transcendenčne, ampak problem je rešljiv (vsaj numerično).
Zgodovina sprememb…
- spremenil: rasta ()
redo ::
Ali je e^(kx) razteg a^x ali obratno? Težko je objektivno reči ...
e^(k x) = a^x, kjer je a = e^k; e^(k x) je razteg e^x in nisem prepričan, da ima kaj veliko za opraviti z objektivnostjo.
Saj, navsezadnje, ponavadi najprej definiraš funkcijo e^x za vse realne x (z limito ali vrsto ali ...) in jo uporabiš za definicijo a^x za vsak pozitiven realen a in za vse realne x. (verjetno se to da definirati tudi drugače, ampak jaz nisem matematik in nimam tako bujne domišljije; seveda lahko stlačiš vse potrebno v definicijo za e^x in slikaš kot da si definiral a^x brez definicije e^x, ampak si res?).
Če recimo gledaš populacijo bakterij 100 bakterij, ki se podvojijo vsako minuto, potem ti zapis N=100*2^(T/60 s) pove več kot pa formula N=100*e^(0.693 T/60 s).
Slednje ni zapisano v zgornji obliki, kar bi bilo N=100*e^(T/86.6s) z značilnim časom 86.6s. Ampak stvar okusa je (in konsenza), ali raje govoriš v razpolovnih, ali v značilnih časih. In ponavadi tudi razpolovni časi niso tako lepo okrogli, da bi to igralo kakšno veliko vlogo pri tej odločitvi.
Ampak k*b^(x/x_0), za recimo b=2, je pa čisto ok.
Eksponentno naravo procesa diktira diferencialna enačba in nisem še videl koga, ki bi reševal le-to z nastavkom b^(k x). Slednje je posebej grozno, saj imaš dva parametra, ki pa sta sklopljena (če nisi umetno postavil b ali pa k na neko vrednost), za razliko od enake exp(c x), kjer imaš en sam parameter (sicer bi lahko trdil, da si postavil b = e, ampak funkcija exp je definirana brez funkcije b^x).
Sicer se v specializiranih področjih uporablja osnova 2 ali 10 (še kakšna druga?), ampak to je bolj zaradi kozmetike (zgodovine?), kot pa zaradi neke globine, IMHO. Razpolovni čas še ima nek pomen, ampak takoj ko ni več spremenljivka čas, to nima več veliko pomena (značilna energija k T, optična globina, ...). Verjetno bi lahko na novo spisal vse skupaj, tako da bi osnova bila druga (recimo 2, če ti je posebej pri srcu), ampak mislim (nisem poskušal), da bi to pripeljalo do vsepovsod štrlečih faktorjev v obliki ln(2).
euler ::
e^(k x) = a^x, kjer je a = e^k; e^(k x) je razteg e^x in nisem prepričan, da ima kaj veliko za opraviti z objektivnostjo.
Saj, navsezadnje, ponavadi najprej definiraš funkcijo e^x za vse realne x (z limito ali vrsto ali ...) in jo uporabiš za definicijo a^x za vsak pozitiven realen a in za vse realne x. (verjetno se to da definirati tudi drugače, ampak jaz nisem matematik in nimam tako bujne domišljije; seveda lahko stlačiš vse potrebno v definicijo za e^x in slikaš kot da si definiral a^x brez definicije e^x, ampak si res?).
Funkcija a^x je definirana brez e^x. Najprej definiraš a^x za naravne x, potem za racionalne, potem pa za realne, kjer za vrednost a^x vzameš kar limito a^y, ko gre y proti x po racionalnih vrednostih.
Funkcijo e^x se lahko definira naknadno, lahko tudi z vrsto.
Tisto z objektivnostjo sem pa mislil takole: e^x=2^(kx), kjer je k=log_2(e). Torej je e^x samo raztegnjen graf funkcije 2^x. Ni res?
Slednje ni zapisano v zgornji obliki, kar bi bilo N=100*e^(T/86.6s) z značilnim časom 86.6s. Ampak stvar okusa je (in konsenza), ali raje govoriš v razpolovnih, ali v značilnih časih. In ponavadi tudi razpolovni časi niso tako lepo okrogli, da bi to igralo kakšno veliko vlogo pri tej odločitvi.
Natanko tako: stvar okusa. Saj ravno to sem hotel reči: ni nobenega razloga, da bi bil e boljši od 2, razen tradicije seveda.
Eksponentno naravo procesa diktira diferencialna enačba in nisem še videl koga, ki bi reševal le-to z nastavkom b^(k x). Slednje je posebej grozno, saj imaš dva parametra, ki pa sta sklopljena (če nisi umetno postavil b ali pa k na neko vrednost), za razliko od enake exp(c x), kjer imaš en sam parameter (sicer bi lahko trdil, da si postavil b = e, ampak funkcija exp je definirana brez funkcije b^x).
Parameter b fiksiraš, recimo b=2.
Diferencialne enačbe, ki se jih dobi v fiziki, so vedno oblike
dy/y = k.
S poudarkom na k. Rešitev te enačbe je funkcija y0*a^(c(x-x0)). Konstanto a lahko izbereš poljubno, c pa dobiš v odvisnosti od a. Na primer, lahko vzameš a=e in c=k.
Razlog, da se potem prevede na e^x, ne tiči v fizikalnem, ampak v matematičnem ozadju: odvod e^x je e^x (kar pa nima nobenega fizikalnega pomena, ker v fiziki vselej nastopi še parameter k, ki ti zabriše vlogo števila e), kar se s pridom uporablja pri reševanju zgornje enačbe.
funkcija b^(k x) ima natanko toliko parametrov kot e^(c x), to je en parameter c. In pa, b^(k x) je lepo definirana tudi brez funkcije e^x.
Razlogi, da se uvaja število e, so matematične narave in ne fizikalne. Funkcija e^x poenostavi računanje (diferencialnih enačb) in je zato tradicionalno bolj uporabljana kot 2^x, ampak nima pa ta funkcija nobenega fizikalnega pomena. Število e NI fizikalna konstanta.
Verjetno bi lahko na novo spisal vse skupaj, tako da bi osnova bila druga (recimo 2, če ti je posebej pri srcu), ampak mislim (nisem poskušal), da bi to pripeljalo do vsepovsod štrlečih faktorjev v obliki ln(2).
Faktorjev ln(2) ne bi bilo, ker bi se absorbirali v koeficient k (namesto k bi pač dobil en drug c).
Zgodovina sprememb…
- spremenil: euler ()
redo ::
Se opravičjujem, ker bom citate spet malenkost pomešal, upam da jim ne odvzemam konteksta. Se seveda strinjam, da je mogoče b^c definirati tudi na način, ki si ga opisal. Sem pozabil na to možnost.
Ampak k ima fizikalen pomen. Zato ne moreš kar preprosto reči, da bi se razni ln(b) absorbirali v k. Če bi v primeru časa še lahko recimo zagovarjal, da čas R C ln(b) pomeni kdaj se kondenzator napolni do 1/b, kaj potem pomeni energija k_B T ln(b)? Ali pa boš čas meril v 1/ln(2) časovnih enotah (in analogno za energijo)?
Da, ampak tvoj prvotni komentar ni govoril o tem, zakaj 2 (ki ima pomen samo za razpolovne čase in morda kje v informatiki, kjer se dela z biti) ali 10, ampak "ena leva osnova a" (kar razumem kot pozitivna realna konstanta a, ker si povedal, da nimaš v mislih konstante z enoto). V tem kontekstu a nima nobenega fizikalnega pomena. Ne samo to, še tistim konstantam, ki bi ga v izrazu imele, lahko odvzame pomen. Ker če se gremo tako, zakaj pa 2 in ne 3527/3 + sqrt(pi/4), ki sta obe ravno tako le matematični konstanti in s fiziko nimata kaj?
In v odvisnosti od k. Seveda je matematično pravilno (v primeru, ko je k = c ln(a)), ampak iz linearne homogene diferencialne enačbe prvega reda z enim konstantnim koeficientom, si dobil rešitev s štirimi parametri (ki nobeden ni prvotni k) od katerih sta dva povezana s prvotnim parametrom k, druga dva pa z začetnim pogojem (moral pa bi pridobiti le eno konstanto integracije). In zdaj ti dam podatke in boš poskušal za svoj model ugotoviti te štiri parametre? Pa saj veš, da ne bo "špilalo". Se boš izgovoril, da boš recimo a in y0 že vnaprej nastavil na sqrt(13) in sin(e) in boš ugotavljal samo dva? In kako boš sedaj pojasnil zakaj ravno sqrt(13) in ne sqrt(13.01) ter zakaj ravno a in y0?
Kako pa šteješ in zakaj "neka leva osnova" b ni tvoj parameter? Od kje si pa potegnil to matematično konstanto in kakšna je njena vrednost ter zakaj?
Razlog je (kot si podobno že povedal), ker je funkcija A*exp(x) (namenoma zapisana brez e) splošna rešitev linearne homogene diferencialne enačbe g'(x)-g(x)=0. B*b^x pač v splošnem ni rešitev te enačbe. Saj zaradi mene lahko pišeš tudi cos_ž(x) = cos(ž x) kot novo funkcijo, ampak to še vedno ne spremeni, da se v ozadju skriva funkcija cos.
Diferencialne enačbe, ki se jih dobi v fiziki, so vedno oblike
dy/y = k.
S poudarkom na k.
Razlog, da se potem prevede na e^x, ne tiči v fizikalnem, ampak v matematičnem ozadju: odvod e^x je e^x (kar pa nima nobenega fizikalnega pomena, ker v fiziki vselej nastopi še parameter k, ki ti zabriše vlogo števila e), kar se s pridom uporablja pri reševanju zgornje enačbe.
Faktorjev ln(2) ne bi bilo, ker bi se absorbirali v koeficient k (namesto k bi pač dobil en drug c).
Ampak k ima fizikalen pomen. Zato ne moreš kar preprosto reči, da bi se razni ln(b) absorbirali v k. Če bi v primeru časa še lahko recimo zagovarjal, da čas R C ln(b) pomeni kdaj se kondenzator napolni do 1/b, kaj potem pomeni energija k_B T ln(b)? Ali pa boš čas meril v 1/ln(2) časovnih enotah (in analogno za energijo)?
Natanko tako: stvar okusa. Saj ravno to sem hotel reči: ni nobenega razloga, da bi bil e boljši od 2, razen tradicije seveda.
Da, ampak tvoj prvotni komentar ni govoril o tem, zakaj 2 (ki ima pomen samo za razpolovne čase in morda kje v informatiki, kjer se dela z biti) ali 10, ampak "ena leva osnova a" (kar razumem kot pozitivna realna konstanta a, ker si povedal, da nimaš v mislih konstante z enoto). V tem kontekstu a nima nobenega fizikalnega pomena. Ne samo to, še tistim konstantam, ki bi ga v izrazu imele, lahko odvzame pomen. Ker če se gremo tako, zakaj pa 2 in ne 3527/3 + sqrt(pi/4), ki sta obe ravno tako le matematični konstanti in s fiziko nimata kaj?
Rešitev te enačbe je funkcija y0*a^(c(x-x0)). Konstanto a lahko izbereš poljubno, c pa dobiš v odvisnosti od a.
In v odvisnosti od k. Seveda je matematično pravilno (v primeru, ko je k = c ln(a)), ampak iz linearne homogene diferencialne enačbe prvega reda z enim konstantnim koeficientom, si dobil rešitev s štirimi parametri (ki nobeden ni prvotni k) od katerih sta dva povezana s prvotnim parametrom k, druga dva pa z začetnim pogojem (moral pa bi pridobiti le eno konstanto integracije). In zdaj ti dam podatke in boš poskušal za svoj model ugotoviti te štiri parametre? Pa saj veš, da ne bo "špilalo". Se boš izgovoril, da boš recimo a in y0 že vnaprej nastavil na sqrt(13) in sin(e) in boš ugotavljal samo dva? In kako boš sedaj pojasnil zakaj ravno sqrt(13) in ne sqrt(13.01) ter zakaj ravno a in y0?
funkcija b^(k x) ima natanko toliko parametrov kot e^(c x), to je en parameter c.
Kako pa šteješ in zakaj "neka leva osnova" b ni tvoj parameter? Od kje si pa potegnil to matematično konstanto in kakšna je njena vrednost ter zakaj?
Razlogi, da se uvaja število e, so matematične narave in ne fizikalne. Funkcija e^x poenostavi računanje (diferencialnih enačb) in je zato tradicionalno bolj uporabljana kot 2^x, ampak nima pa ta funkcija nobenega fizikalnega pomena. Število e NI fizikalna konstanta.
Razlog je (kot si podobno že povedal), ker je funkcija A*exp(x) (namenoma zapisana brez e) splošna rešitev linearne homogene diferencialne enačbe g'(x)-g(x)=0. B*b^x pač v splošnem ni rešitev te enačbe. Saj zaradi mene lahko pišeš tudi cos_ž(x) = cos(ž x) kot novo funkcijo, ampak to še vedno ne spremeni, da se v ozadju skriva funkcija cos.
euler ::
Ampak k ima fizikalen pomen. Zato ne moreš kar preprosto reči, da bi se razni ln(b) absorbirali v k.
Nisem šel preverjat v fizikalne formule, ampak mislim, da k nima fizikalnega pomena. Seveda si dobrodošel, da daš kakšen primer, npr. iz elektrike (jaz se ga ne morem spomnit) - lahko tudi tistega s kondenzatorjem malo bolj natančno napišeš (vsaj dif. enačbo, da vidimo, kaj je tisti k) ...
Da, ampak tvoj prvotni komentar ni govoril o tem, zakaj 2 (ki ima pomen samo za razpolovne čase in morda kje v informatiki, kjer se dela z biti) ali 10, ampak "ena leva osnova a" (kar razumem kot pozitivna realna konstanta a, ker si povedal, da nimaš v mislih konstante z enoto). V tem kontekstu a nima nobenega fizikalnega pomena. Ne samo to, še tistim konstantam, ki bi ga v izrazu imele, lahko odvzame pomen. Ker če se gremo tako, zakaj pa 2 in ne 3527/3 + sqrt(pi/4), ki sta obe ravno tako le matematični konstanti in s fiziko nimata kaj?
Točno tako!
Saj nisem izpostavljal 2, dal sem jo samo kot primer. Z isto pravico bi lahko tudi vzel 23.2312313422342. Vse te konstante (vključno z e) so brez fizikalnega pomena.
Rešitev te enačbe je funkcija y0*a^(c(x-x0)). Konstanto a lahko izbereš poljubno, c pa dobiš v odvisnosti od a.
In v odvisnosti od k. Seveda je matematično pravilno (v primeru, ko je k = c ln(a)), ampak iz linearne homogene diferencialne enačbe prvega reda z enim konstantnim koeficientom, si dobil rešitev s štirimi parametri (ki nobeden ni prvotni k) od katerih sta dva povezana s prvotnim parametrom k, druga dva pa z začetnim pogojem (moral pa bi pridobiti le eno konstanto integracije). In zdaj ti dam podatke in boš poskušal za svoj model ugotoviti te štiri parametre? Pa saj veš, da ne bo "špilalo". Se boš izgovoril, da boš recimo a in y0 že vnaprej nastavil na sqrt(13) in sin(e) in boš ugotavljal samo dva? In kako boš sedaj pojasnil zakaj ravno sqrt(13) in ne sqrt(13.01) ter zakaj ravno a in y0?
Nisem te dobro zastopil. y0 in x0 sta podatka (začetno stanje), k je podatek. Rešitev je seveda y0*e^(k(x-x0)). Ampak tu konstanta k nima nobenega fizikalnega pomena, tako da z isto pravico lahko zapišemo tudi s kakšno drugo osnovo, npr. 2 ali 2342.432423.
Kako pa šteješ in zakaj "neka leva osnova" b ni tvoj parameter? Od kje si pa potegnil to matematično konstanto in kakšna je njena vrednost ter zakaj?
Vrednost b fiksiraš, npr. b=321321.32131313. Tradicionalno se uporablja b=2.71828.
Razlog je (kot si podobno že povedal), ker je funkcija A*exp(x) (namenoma zapisana brez e) splošna rešitev linearne homogene diferencialne enačbe g'(x)-g(x)=0. B*b^x pač v splošnem ni rešitev te enačbe.
Res je, ampak to je "matematični" razlog. V fiziki enačbe g'(x)-g(x)=0 ne boš srečal.
redo ::
Nisem šel preverjat v fizikalne formule, ampak mislim, da k nima fizikalnega pomena. Seveda si dobrodošel, da daš kakšen primer, npr. iz elektrike (jaz se ga ne morem spomnit) - lahko tudi tistega s kondenzatorjem malo bolj natančno napišeš (vsaj dif. enačbo, da vidimo, kaj je tisti k) ...
Ah, kako da ne? Saj ima enoto. Praznjenje kondenzatorja skozi upor:
I'(t) + 1/(R C) I(t) = 0.
Čas RC (ki je mimogrede 1/k) je značilni čas v katerem se praznijo/polnijo kondenzatorji (in ne razlog ni preprosto to, da pač nastopa v eksponentu), kar čas RC ln( exp[-16]) pač ni.
Nisem te dobro zastopil. y0 in x0 sta podatka (začetno stanje), k je podatek. Rešitev je seveda y0*e^(k(x-x0)). Ampak tu konstanta k nima nobenega fizikalnega pomena, tako da z isto pravico lahko zapišemo tudi s kakšno drugo osnovo, npr. 2 ali 2342.432423.
Res? Kateri podatek pa imaš, ko začneš merit y (= y0*a^[c(x-x0)]) v odvisnosti od x? Ti zmeriš y_i(x_i) za i=1,...,n, potem pa moraš iz teh vrednosti povedat, kakšno vrednost imajo y0, a, c, x0. Ampak v tem modelu je parametrov preveč, zato so med seboj sklopljeni. Za y0, a, c in x0 imaš tako na voljo ogromno vrednosti. Ampak ti mi praviš, da ti parametri itak nimajo fizikalnega pomena (kateri parameter v tej rešitvi pa ga potem sploh ima?). Mimogrede, nekatere standardne metode ti bodo poskušale to dopovedat (da imaš preveč parametrov) in ti bodo pravile, da nekaj ni v redu z eno matriko.
Vrednost b fiksiraš, npr. b=321321.32131313. Tradicionalno se uporablja b=2.71828.
In zakaj ravno vrednost 321321.32131313? Tradicionalno se ne uporablja 2.71828 ampak e, oziroma se uporablja funkcija exp.
Res je, ampak to je "matematični" razlog. V fiziki enačbe g'(x)-g(x)=0 ne boš srečal.
Ah, če si prebral ta komentar, si jo že videl. V zgornjo enačbo vpeljem nove spremenljivke in funkcije, tako da velja
t=RC x; I(t) = I(ž) g(t/RC) oziroma = I(ž) g(x), je ž nek čas (in je konstanta) in velja še g(ž/RC) = 1?
Je to že matematika in ne velja?
redo ::
Res je, ampak to je "matematični" razlog. V fiziki enačbe g'(x)-g(x)=0 ne boš srečal.
Ah, če si prebral ta komentar, si jo že videl. V zgornjo enačbo vpeljem nove spremenljivke in funkcije, tako da velja
t=RC x; I(t) = I(ž) g(t/RC) oziroma = I(ž) g(x), je ž nek čas (in je konstanta) in velja še g(ž/RC) = 1?
Je to že matematika in ne velja?
Se opravičujem, nastala enačba je g'(x)+g(x)=0. Če pa se uvede t=-RC x in I(t) = I(ž) g(-t/RC)=I(ž)g(x), potem pa se dobi obliko z minusom. Veljati mora še g(-ž/RC)=1.
JanK ::
No, ja, obe enacbi, $f'(t)=-a\,f(t)$ (napaka se odpravlja) in $f'(t)=b\,f(t)$ (napaka se odpravlja) dobis v fiziki (pri cemer predpostavimo, da sta $a$ (napaka se odpravlja) in $b$ (napaka se odpravlja) pozitivni kolicini). Primer prve je, kot ze receno, praznjenje ali polnjenje kondenzatorja, radioaktiven razpad,... primer druge pa recimo narascanje neke populacije brez upostevanja smrti.
Uporaba $e$ (napaka se odpravlja) kot osnova je res konvencija in mirno bi lahko uporabljali 2 ali pa katerokoli drugo konstanto. Ampak glede na to, koliko izrazov je precej bolj enostavnih z $e$ (napaka se odpravlja) in bi z uporabo druge konstante moral za sabo vleci se nek faktor (ki bi bil itak povezan z $e$ (napaka se odpravlja) ), je takorekoc "naravno" vzeti $e$ (napaka se odpravlja) in ne "zblj".
), je takorekoc "naravno" vzeti $e$ (napaka se odpravlja) in ne "zblj".
Kar se enot tice: enota $a$ (napaka se odpravlja) in $b$ (napaka se odpravlja) mora biti reciprocna enoti neodvisne spremenljivke - tiste po kateri odvajas - in itak nima zveze z osnovo eksponentne funkcije. Ce gre za odvod po casu, mora biti enota 1/[cas], ce po dolzini, 1/[dolzina],... Kaj pa je pomen vrednosti $a$ (napaka se odpravlja) in $b$ (napaka se odpravlja) pa je odvisno od primera. Pri praznjenju kondenzatorja, je "konvencionalni" parameter znacilni cas, ker niti ni tako zanimivo vedeti kdaj pade napetost na polovico (stromarji popravite me, ce se motim). Pri radioaktivnem razpadu se seveda uporablja tudi razpadna konstanta, ampak tam se jo raje izrazi s "konvencionalnim" parametrom razpolovni cas, ki je pri radioaktivnem razpadu bolj zanimiv in pove vec.
Uporaba $e$ (napaka se odpravlja) kot osnova je res konvencija in mirno bi lahko uporabljali 2 ali pa katerokoli drugo konstanto. Ampak glede na to, koliko izrazov je precej bolj enostavnih z $e$ (napaka se odpravlja) in bi z uporabo druge konstante moral za sabo vleci se nek faktor (ki bi bil itak povezan z $e$ (napaka se odpravlja)
Kar se enot tice: enota $a$ (napaka se odpravlja) in $b$ (napaka se odpravlja) mora biti reciprocna enoti neodvisne spremenljivke - tiste po kateri odvajas - in itak nima zveze z osnovo eksponentne funkcije. Ce gre za odvod po casu, mora biti enota 1/[cas], ce po dolzini, 1/[dolzina],... Kaj pa je pomen vrednosti $a$ (napaka se odpravlja) in $b$ (napaka se odpravlja) pa je odvisno od primera. Pri praznjenju kondenzatorja, je "konvencionalni" parameter znacilni cas, ker niti ni tako zanimivo vedeti kdaj pade napetost na polovico (stromarji popravite me, ce se motim). Pri radioaktivnem razpadu se seveda uporablja tudi razpadna konstanta, ampak tam se jo raje izrazi s "konvencionalnim" parametrom razpolovni cas, ki je pri radioaktivnem razpadu bolj zanimiv in pove vec.
euler ::
Ah, kako da ne? Saj ima enoto. Praznjenje kondenzatorja skozi upor:
I'(t) + 1/(R C) I(t) = 0.
Čas RC (ki je mimogrede 1/k) je značilni čas v katerem se praznijo/polnijo kondenzatorji (in ne razlog ni preprosto to, da pač nastopa v eksponentu), kar čas RC ln( exp[-16]) pač ni
Kaj je to značilni čas? Kaj je njegov fizikalni pomen?
A. Smith ::
Fizikalni pomen produkta RC je čas polnjenja kondenzatorja, vezanega zaporedno z uporom (upornost vedno obstaja, vsaj parazitna) na konstantno napetost. Napetost pri polnjenju kondenzatorja se spreminja po funkciji u(t)=U*(1-e^(-t/RC)), pri čemer je U napetost vira.
Kondenzator se smatra za polnega, ko čas (torej spremenljivka t) doseže 4*RC. 1-e^(-4)=0.98, se pravi je ob tem času napetost na kondenzatorju 98 odstotna. Dlje se pač ne čaka, ker narašča 1-e^(-x) zelo počasi.
Kondenzator se smatra za polnega, ko čas (torej spremenljivka t) doseže 4*RC. 1-e^(-4)=0.98, se pravi je ob tem času napetost na kondenzatorju 98 odstotna. Dlje se pač ne čaka, ker narašča 1-e^(-x) zelo počasi.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
Thomas ::
Kje smo ostali?
rasta pravi nekako takole: "y os je tam, kjer se tangenta vzpenja točno pod 45°!"
To je razbral iz para x osi IN grafa eksponentnice - drži?
rasta pravi nekako takole: "y os je tam, kjer se tangenta vzpenja točno pod 45°!"
To je razbral iz para x osi IN grafa eksponentnice - drži?
Man muss immer generalisieren - Carl Jacobi
euler ::
Fizikalni pomen produkta RC je čas polnjenja kondenzatorja, vezanega zaporedno z uporom (upornost vedno obstaja, vsaj parazitna) na konstantno napetost. Napetost pri polnjenju kondenzatorja se spreminja po funkciji u(t)=U*(1-e^(-t/RC)), pri čemer je U napetost vira.
Kondenzator se smatra za polnega, ko čas (torej spremenljivka t) doseže 4*RC. 1-e^(-4)=0.98, se pravi je ob tem času napetost na kondenzatorju 98 odstotna. Dlje se pač ne čaka, ker narašča 1-e^(-x) zelo počasi.
He he, malo si se prigoljufal čez. 98% seveda ni 100%. Pa saj tudi ne zahtevam 100%, ker vem, da bi za to porabil neskončno časa. Ampak zakaj pa ravno 98 in ne recimo 97? Zato, ker bi za 97% dobil grdo cifro, recimo t=3.82234234*RC. Za 98% pa dobiš lepo 4*RC, kar itak ni presenetljivo, če si pa vzel ravno 98% s tem namenom. In potem lahko rečeš, glej kakšno naključje, čas je ravno 4*RC in ne recimo 4.00001*RC!
Thomas, zakaj pa se zame ne zmeniš? Pa tako sem se potrudil zate.
Zgodovina sprememb…
- spremenil: euler ()
A. Smith ::
In potem lahko rečeš, glej kakšno naključje, čas je ravno 4*RC in ne recimo 4.00001*RC!
Ne ga no bixat! To, kar si napisal, je samoumevno. 3-4 časovne konstante je pač smiselno čakat. Jaz sem vzel 4, vendar vrednost ni zabetonirana.
Je pa konstanta pomembna, ker velja za vsako vrednost elementov. Vsakič je čas, pri katerem se kond napolni (1-1/e), določen s produktom R*C.
Vprašanje je, če je mogoče priti do tako enostavnega zapisa z neko drugo osnovo, kot je e?
Po formuli dobimo u(t)=U*(1-10^[(-t/RC)*ln 10]), oz. u(t)=U*(1-10^[(-t/RC)* 2,3])
(ok - kapiram; hočeš reči, da se tisto dodatno konstanto tako ali tako kasneje doda. Vendar meni 97% vrednost tako ali tako nič ne pomeni.)
Zapis, ki ga zagovarja JanK se mi še vedno zdi preprostejši in bolj uporaben.
"Be professional, be polite,
but have a plan to kill everyone you meet".
- General James Mattis
but have a plan to kill everyone you meet".
- General James Mattis
Zgodovina sprememb…
- spremenil: A. Smith ()
euler ::
Ne ga no bixat! To, kar si napisal, je samoumevno. 3-4 časovne konstante je pač smiselno čakat. Jaz sem vzel 4, vendar vrednost ni zabetonirana.
Potem se razumeva. Lahko vzamemo tudi npr. T=RC*3.9 in to proglasimo za čas polnjenja. Ali pa T=3.89182*RC. V slednjem primeru dobimo
U=U_0*e^(-t/RC)=U_0*e^(-t/T*3.89182)=U_0*49^(-t/T)=U_0*7^(-2t/T).
Mar ni to lepa formula? Magična osnova, ki naredi vse cifre okrogle, je v tem primeru 7. Čas T ti pa ravno pove, kdaj napetost pade na 1/49 prvotne napetosti.
Vprašanje je, če je mogoče priti do tako enostavnega zapisa z neko drugo osnovo, kot je e?
Torej, 7 je iskana osnova. Glej zgoraj.
Če vzamem osnovo 7, potem v enačbah seveda ne bo več RC, ampak ž*RC za neko čudno konstanto ž (ž=ln 7 oziroma nekaj takega). Ampak to te kot fizika itak ne moti (kvečjemu kot matematika, ker je več za računat), ker imata konstanti RC in ž*RC itak isti fizikalni pomen (če za malenkost spremenimo definicijo časa polnenja).
Razumel?
Zgodovina sprememb…
- spremenil: euler ()
redo ::
Kaj je to značilni čas? Kaj je njegov fizikalni pomen?
To je skala, na kateri se v RC krogu nekaj zgodi. Z neko "levo osnovo" b, RC ln(b) to pač ni. V kolikšnem času se kondenzator napolni/sprazni? V prvem približku (v prvem redu ali v linearnem približku) v času RC (in ne v RC ln(b)).
Saj sem že napisal, matematično se lahko igraš igrice, in napišeš obskurno y0 * a^(c (x - x0)) ampak bo prišlo za tabo in te bo pošteno ugriznilo. Če ne prej, pri luščenju parametrov ali "fitanju", kjer boš moral na podlagi nekega fizikalnega razloga nastaviti dva od parametrov (in me prav zanima, kakšna bo tvoja utemeljitev izbire brezdimenzijskega parametra a). Matematika ti ga pač ne bo dala.
He he, malo si se prigoljufal čez. 98% seveda ni 100%. Pa saj tudi ne zahtevam 100%, ...
Saj se zavedaš, da so vse te formule le približek (sicer zelo dober približek, ampak še vedno samo približek)?
euler ::
To je skala, na kateri se v RC krogu nekaj zgodi. Z neko "levo osnovo" b, RC ln(b) to pač ni. V kolikšnem času se kondenzator napolni/sprazni? V prvem približku (v prvem redu ali v linearnem približku) v času RC (in ne v RC ln(b)).
Linearni približek je nesporno RC in ne RC*ln(b). Ampak tebi to bolj malo pomaga. Za začetek je nekaj, ampak v praksi pa boš rabil malo bolj natančne izračune. Recimo, koristil bi ti podatek, če je recimo začetna napetost 10V, kdaj napetost pade na 1V. In tu bi ti prav prišla osnova 10. Ali pa, kdaj se napetost razpolovi. ITD. Tu bi rabil osnovo 2. Pri vseh teh primerih bi največkrat rabil celoštevilsko osnovo, ne pa e.
Problem je, ker enotne osnove ne moremo izbrati (kolebamo med 10, 2 in ostalimi), za vsak račun svojo osnovo pa tudi ni pametno, ker je težko računat in pretvarjat osnove in rata en kaos. Treba je imet enotno osnovo. Pri računanju se najbolj primerna izkaže e (predvsem za diferencialne enačbe), zato se uporablja kar e.
Saj se zavedaš, da so vse te formule le približek (sicer zelo dober približek, ampak še vedno samo približek)?
Seveda se, zakaj pa to sprašuješ?
Zgodovina sprememb…
- spremenil: euler ()
redo ::
Linearni približek je nesporno RC in ne RC*ln(b). Ampak tebi to bolj malo pomaga. Za začetek je nekaj, ampak v praksi pa boš rabil malo bolj natančne izračune.
V kateri praksi to? Tam debatirajo, ali je kondenzator poln pri 98% ali pri 97% ... katere napetosti že?
Recimo, koristil bi ti podatek, če je recimo začetna napetost 10V, kdaj napetost pade na 1V. In tu bi ti prav prišla osnova 10. Ali pa, kdaj se napetost razpolovi. ITD. Tu bi rabil osnovo 2. Pri vseh teh primerih bi največkrat rabil celoštevilsko osnovo, ne pa e.
V vseh namišljenih šolskih primerih z lepimi naravnimi števili te res zanimajo takšne stvari. Še kje drugje? In potem boš razglasil RC ln(2) za novi značilni čas in se vse lepo izide, ker napetost iz 10V pade na 5V v enem značilnem času. Potem te vprašam v kolikšnem času pa pade na 1V in je odgovor enak (v enem značilnem času), ali kako?
Treba je imet enotno osnovo. Pri računanju se najbolj primerna izkaže e (predvsem za diferencialne enačbe), zato se uporablja kar e.
Glej, zaradi mene lahko pišeš cos_š(p x) in se igraš, da je ta funkcija boljša in bolj "naravna", kot cos( w x ). V podkrepitev si lahko izmisliš še namišljene primere, kako se periode ali kaj jaz vem, lepo preslikajo v množico celih števil.
Bom pa vprašal tako, kje v diferencialni enačbi
I' + I/RC=0
vidiš osnovo b ali e? Jaz bi prej rekel, da je prelepo (ne)naključje v matematiki, da je exp(x) (kot rešitev g'-g=0) = e^x (kot e na potenco x).
Morda pa lahko poskusiš uvesti podobne parametre še pri Besselovih funkcijah, Legendrovih polinomih, ...
rasta ::
rasta pravi nekako takole: "y os je tam, kjer se tangenta vzpenja točno pod 45°!"
To je razbral iz para x osi IN grafa eksponentnice - drži?
Točno tako. Ordinata je tam, kjer je kot tangente in abcise 45˚ ter oddaljenost od abcise 1 (drugače lahko določimo faktor raztega merila osi).
Vredno ogleda ...
| Tema | Ogledi | Zadnje sporočilo | |
|---|---|---|---|
| Tema | Ogledi | Zadnje sporočilo | |
| » | matematkaOddelek: Šola | 3382 (2361) | lebdim |
| » | Matematično vprašanje (strani: 1 2 )Oddelek: Šola | 11996 (10062) | joze67 |
| » | PI is wrong! (strani: 1 2 3 4 )Oddelek: Znanost in tehnologija | 19144 (12448) | modicr |
| » | Matematika - pomoč (strani: 1 2 3 )Oddelek: Šola | 29004 (25579) | daisy22 |
| » | Genetski algoritemOddelek: Programiranje | 3036 (2612) | rasta |